Bài 2.9 trang 64 SBT hình học 11

Giải bài 2.9 trang 64 sách bài tập hình học 11. Cho tứ diện S.ABC có D, E lần lượt trung điểm AC, BC và G là trọng tâm tam giác ABC...

Đề bài

Cho tứ diện \(SABC\) có \(D\), \(E\) lần lượt trung điểm \(AC\), \(BC\) và \(G\) là trọng tâm tam giác \(ABC\). Mặt phẳng \((\alpha)\) qua \(AC\) cắt \(SE\), \(SB\) lần lượt tại \(M\), \(N\). Một mặt phẳng \((\beta)\) qua \(BC\) cắt \(SD\) và \(SA\) lần lượt tại \(P\) và \(Q\).

a) Gọi \(I = AM \cap DN\), \(J = BP \cap EQ\). Chứng minh bốn điểm \(S\), \(I\), \(J\), \(G\) thẳng hàng.

b) Giả sử \(AN \cap DM = K\), \(BQ \cap EP = L\). Chứng minh ba điểm \(S\), \(K\), \(L\) thẳng hàng.

Phương pháp giải - Xem chi tiết

Để chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó cùng thuộc hai mặt phẳng phân biệt

Lời giải chi tiết

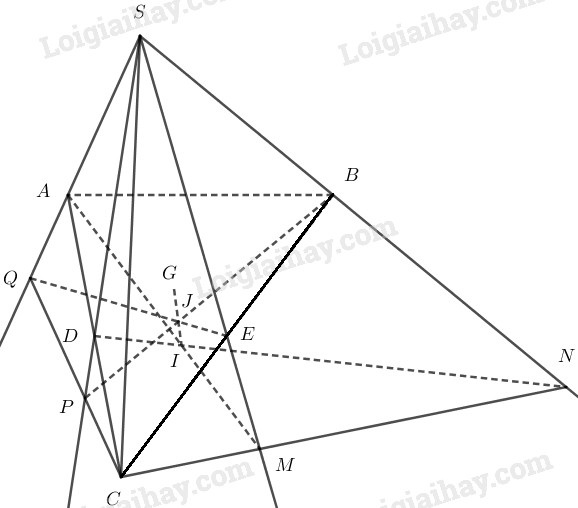
Ta thấy:

+ \(G\) là trọng tâm tam giác \(ABC\) \(\Rightarrow G \in BD \Rightarrow G \in BD\).

+ \(I \in DN\) (theo cách dựng hình).

+ \(J \in BP\) (theo cách dựng hình).

\(\Rightarrow S, I, J, G \in (SPN)\)

Tương tự \( S, I, J, G \in (SQM)\)

Vậy \(S, I, J, G\) là điểm chung của \((SPN)\) và \((SQM)\).

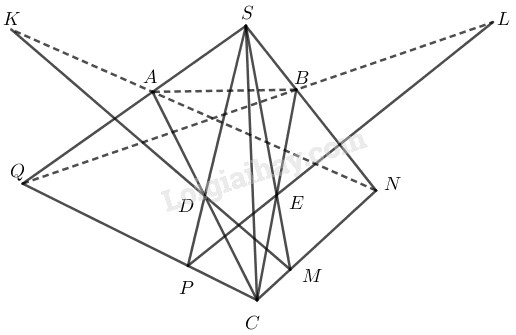
Ta thấy:

+ \(S = PD \in EM\)

+ \(K \in DM\)

+ \(L \in PE\)

\(\Rightarrow S, K, L \in (SPM)\)

Tương tự \(S, K, L \in (SQN)\)

Vậy \(S, K, L\) là điểm chung của \((SPM)\) và \((SQN)\).

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 7 phiếu

Bài tiếp theo

Bài 2.8 trang 64 SBT hình học 11
Giải bài 2.8 trang 64 sách bài tập hình học 11. Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α) và (β) sao cho OA và OB lần lượt cắt (β) tại A’ và B’...
Bài 2.7 trang 64 SBT hình học 11
Giải bài 2.7 trang 64 sách bài tập hình học 11. Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng hàng.
Bài 2.6 trang 64 SBT hình học 11
Giải bài 2.6 trang 64 sách bài tập hình học 11. Cho hình chóp S.ABCD. M và N tương ứng là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).
Bài 2.5 trang 64 SBT hình học 11
Giải bài 2.5 trang 64 sách bài tập hình học 11. Cho hình chóp S. ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp.
Bài 2.4 trang 63 SBT hình học 11
Giải bài 2.4 trang 63 sách bài tập hình học 11. Cho tứ diện ABCDcó các điểm M và N lần lượt là trung điểm của ACvà BC. Lấy điểm K thuộc đoạn BD( K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).
Bài 2.3 trang 63 SBT hình học 11
Giải bài 2.3 trang 63 sách bài tập hình học 11. Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)...
Bài 2.2 trang 63 SBT hình học 11
Giải bài 2.2 trang 63 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD...
Bài 2.1 trang 63 SBT hình học 11
Giải bài 2.1 trang 63 sách bài tập hình học 11. Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD . Gọi I và J tương ứng là hai điểm trên cạnh BC và BD sao cho IJ không song song với CD