Bài 2.10 trang 67 SBT hình học 11

Giải bài 2.10 trang 67 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là hình hình hành ABCD. Tìm giao tuyến của các cặp mặt phẳng sau đây...

Lựa chọn câu để xem lời giải nhanh hơn

Cho hình chóp \(S.ABCD\) có đáy là hình hình hành \(ABCD\). Tìm giao tuyến của các cặp mặt phẳng sau đây:

LG a

\((SAC)\) và \((SBD)\)

Phương pháp giải:

Muốn tìm giao tuyến của hai mặt phẳng ta tìm hai điểm chung của chúng.

Lời giải chi tiết:

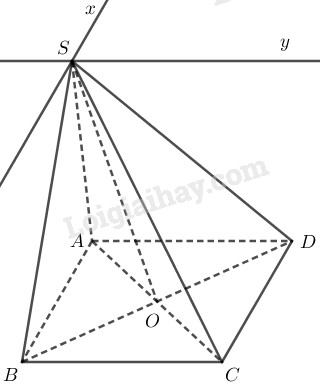
Ta có: \(S\in (SAC)\cap(SBD)\)

Gọi \(AC \cap BD = O\)

Mà \(AC\subset (SAC)\), \(BD\subset (SBD)\) \(\Rightarrow O\in (SAC)\cap(SBD)\)

\(\Rightarrow (SAC) \cap (SBD) = SO\).

LG b

\((SAB)\) và \((SCD)\)

Phương pháp giải:

Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng \(d\) và \(d’\) song song với nhau:

- Tìm điểm chung của hai mặt phẳng

- Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với \(d\) và \(d’\).

Lời giải chi tiết:

Ta có: \(S\in (SAB)\cap(SCD)\)

Ta lại có:

\(\left\{ \begin{array}{l}AB \subset (SAB)\\CD \subset (SCD)\\AB\parallel CD\end{array} \right.\)

\(\Rightarrow (SAB)\cap (SCD)=Sx,\)

\(Sx\parallel AB\parallel CD\).

LG c

\((SAD)\) và \((SBC)\).

Phương pháp giải:

Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng \(d\) và \(d’\) song song với nhau:

- Tìm điểm chung của hai mặt phẳng

- Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với \(d\) và \(d’\).

Lời giải chi tiết:

Ta có: \(S\in (SAD)\cap(SBC)\)

Ta lại có:

\(\left\{ \begin{array}{l}AD \subset (SAD)\\BC \subset (SBC)\\AD\parallel BC\end{array} \right.\)

\(\Rightarrow (SAD)\cap (SBC)=Sy,\)

\(Sy\parallel AD\parallel BC\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài 2.11 trang 67 SBT hình học 11
Giải bài 2.11 trang 67 sách bài tập hình học 11. Cho tứ diện ABCD. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao cho...
Bài 2.12 trang 67 SBT hình học 11
Giải bài 2.12 trang 67 sách bài tập hình học 11. Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC, M là một điểm tùy ý trên cạnh AD...
Bài 2.13 trang 68 SBT hình học 11
Giải bài 2.13 trang 68 sách bài tập hình học 11. Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
Bài 2.14 trang 68 SBT hình học 11
Giải bài 2.14 trang 68 sách bài tập hình học 11. Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng IJ//CD.
Bài 2.15 trang 68 SBT hình học 11
Giải bài 2.15 trang 68 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy là AD và BC. Biết AD = a, BC = b...