-
ĐẠI SỐ VÀ GIẢI TÍCH- SBT TOÁN 11
-
HÌNH HỌC SBT - TOÁN 11
-
Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
- Bài 1+Bài 2: Phép biến hình. Phép tịnh tiến
- Bài 3: Phép đối xứng trục
- Bài 4: Phép đối xứng tâm
- Bài 5: Phép quay
- Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Bài 7: Phép vị tự
- Bài 8: Phép đồng dạng
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Câu hỏi và bài tập
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Đề toán tổng hợp
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Câu hỏi trắc nghiệm
-
Chương 2: Đường thẳng và mặt phẳng trong không gian quan hệ song song
- Bài 1: Đại cương về đường thằng và mặt phẳng
- Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3: Đường thẳng và mặt phẳng song song
- Bài 4: Hai mặt phẳng song song
- Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Câu hỏi và bài tập
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Đề toán tổng hợp
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Câu hỏi trắc nghiệm
-
Chương 3: Vecto trong không gian. Quan hệ vuông góc trong không gian
-
Ôn tập cuối năm Hình học 11
-
Bài 2.5 trang 64 SBT hình học 11
Giải bài 2.5 trang 64 sách bài tập hình học 11. Cho hình chóp S. ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp.
Đề bài
Cho hình chóp \(S. ABCD\). Lấy \(M\), \(N\) và \(P\) lần lượt là các điểm trên các đoạn \(SA\), \(AB\) và \(BC\) sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng \((MNP)\) với các cạnh của hình chóp.
Phương pháp giải - Xem chi tiết
Ta lần lượt tìm giao điểm của mặt phẳng \((MNP)\) với các đường thẳng chứa các cạnh của hình chóp.
Muốn tìm giao điểm của mặt phẳng \((\alpha)\) với đường thẳng \(d\):
- Tìm đường thẳng \(d’\) sao cho \(d’\in (\alpha)\) và \(d, d’\) cùng thuộc một mặt phẳng.
- Giao điểm \(d\) và \(d’\) là giao điểm của mặt phẳng \((\alpha)\) với đường thẳng \(d\).
Lời giải chi tiết
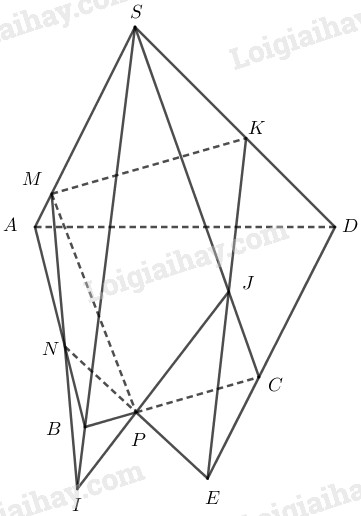
Ta có giao điểm của \( (MNP)\) với \(SA, AB, BC\) lần lượt là \(M, N, P\).
Trong \((SAB)\) kéo dài \(MN\) và \(SB\), khi đó gọi \(I=MN\cap SB\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}I \in MN,MN \subset (MNP) \Rightarrow I \in (MNP)\\I \in SB\end{array} \right.\\ \Rightarrow I = (MNP) \cap SB\end{array}\)
Trong \((ABCD)\) kéo dài \(NP\) và kéo dài \(CD\), khi đó gọi \(E=NP\cap CD\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}E \in NP,NP \subset (MNP) \Rightarrow E \in (MNP)\\E \in CD\end{array} \right.\\ \Rightarrow E = (MNP) \cap CD\end{array}\)
Trong \((MNP)\) hay cũng là \((MIP)\) kéo dài \(IP\), khi đó gọi \(J=IP\cap SC\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}J \in IP,IP \subset (MNP) \Rightarrow J \in (MNP)\\J \in SC\end{array} \right.\\ \Rightarrow J = (MNP) \cap SC\end{array}\)
Trong \((SCD)\) kéo dài \(EJ\) gọi \(K=EJ\cap SD\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}K \in {\rm{EJ}},{\rm{EJ}} \subset (MNP) \Rightarrow K \in (MNP)\\K \in SD\end{array} \right.\\ \Rightarrow K = (MNP) \cap SD\end{array}\).
Chú ý:
Trong bài này ta chỉ xét trường hợp thông thường là khi lấy các điểm bất kì mà khi kéo dài các đường thẳng có thể cắt nhau, tức là MN cắt được SB. Còn trường hợp MN//SB thì thuộc nội dung các bài sau nên ta không xét đến.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2.6 trang 64 SBT hình học 11
- Bài 2.7 trang 64 SBT hình học 11
- Bài 2.8 trang 64 SBT hình học 11
- Bài 2.9 trang 64 SBT hình học 11
- Bài 2.4 trang 63 SBT hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
