Bài 2.1 trang 63 SBT hình học 11

Giải bài 2.1 trang 63 sách bài tập hình học 11. Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD . Gọi I và J tương ứng là hai điểm trên cạnh BC và BD sao cho IJ không song song với CD

Đề bài

Cho tứ diện \(ABCD\) và điểm \(M\) thuộc miền trong của tam giác \(ACD\). Gọi \(I\) và \(J\) tương ứng là hai điểm trên cạnh \(BC\) và \(BD\) sao cho \(IJ\) không song song với \(CD\).

a) Hãy xác định giao tuyến của hai mặt phẳng \((IJM)\) và \((ACD)\).

b) Lấy \(N\) là điểm thuộc miền trong của tam giác \(ABD\) sao cho \(JN\) cắt đoạn \(AB\) tại \(L\). Tìm giao tuyến của hai mặt phẳng \((MNJ)\) và \((ABC)\).

Phương pháp giải - Xem chi tiết

Cách xác định giao tuyến của hai mặt phẳng:

- Xác định điểm chung thứ nhất dễ nhận thấy.

- Tìm hai đường thẳng lần lượt thuộc hai mặt phẳng và chúng cắt nhau.

- Tìm giao điểm của hai đường thẳng đó ta được giao điểm thứ hai của hai mặt phẳng.

Lời giải chi tiết

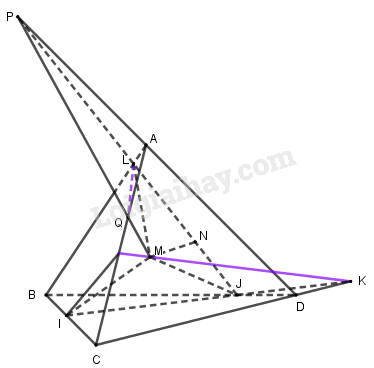
a) Nhận xét: Do IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.

Trong \((BCD)\), gọi \(K = IJ \cap CD\).

Ta có: \(M\) là điểm chung thứ nhất của \((ACD)\) và \((IJM)\);

\(\left\{ \matrix{
K \in IJ \hfill \cr
IJ \subset \left( {MIJ} \right) \hfill \cr} \right. \Rightarrow K \in \left( {MIJ} \right)\) và \(\left\{ \matrix{K \in CD \hfill \cr C{\rm{D}} \subset \left( {AC{\rm{D}}} \right) \hfill \cr} \right. \Rightarrow K \in \left( {AC{\rm{D}}} \right)\)

Vậy \(\left( {MIJ} \right) \cap \left( {ACD} \right) = MK\)

b) Với \(L = JN \cap AB\) ta có:

\(\left\{ \matrix{
L \in JN \hfill \cr
JN \subset \left( {MNJ} \right) \hfill \cr} \right. \Rightarrow L \in \left( {MNJ} \right)\)

\(\left\{ \matrix{
L \in AB \hfill \cr
AB \subset \left( {ABC} \right) \hfill \cr} \right. \Rightarrow L \in \left( {ABC} \right)\)

Như vậy \(L \) là điểm chung thứ nhất của hai mặt phẳng \((MNJ) \) và \((ABC)\)

Gọi \(P = JL \cap A{\rm{D}},Q = PM \cap AC\)

Ta có:

\(\left\{ \matrix{
Q \in PM \hfill \cr
PM \subset \left( {MNP} \right) \hfill \cr} \right. \Rightarrow Q \in \left( {MNJ} \right)\)

Và \(\left\{ \matrix{Q \in AC \hfill \cr AC \subset \left( {ABC} \right) \hfill \cr} \right. \Rightarrow Q \in \left( {ABC} \right)\)

Nên \(Q\) là điểm chung thứ hai của \((MNJ)\) và \((ABC)\)

Vậy \(LQ = \left( {ABC} \right) \cap \left( {MNJ} \right)\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 2.2 trang 63 SBT hình học 11
Giải bài 2.2 trang 63 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD...
Bài 2.3 trang 63 SBT hình học 11
Giải bài 2.3 trang 63 sách bài tập hình học 11. Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)...
Bài 2.4 trang 63 SBT hình học 11
Giải bài 2.4 trang 63 sách bài tập hình học 11. Cho tứ diện ABCDcó các điểm M và N lần lượt là trung điểm của ACvà BC. Lấy điểm K thuộc đoạn BD( K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).
Bài 2.5 trang 64 SBT hình học 11
Giải bài 2.5 trang 64 sách bài tập hình học 11. Cho hình chóp S. ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp.
Bài 2.6 trang 64 SBT hình học 11
Giải bài 2.6 trang 64 sách bài tập hình học 11. Cho hình chóp S.ABCD. M và N tương ứng là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).
Bài 2.7 trang 64 SBT hình học 11
Giải bài 2.7 trang 64 sách bài tập hình học 11. Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng hàng.
Bài 2.8 trang 64 SBT hình học 11
Giải bài 2.8 trang 64 sách bài tập hình học 11. Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α) và (β) sao cho OA và OB lần lượt cắt (β) tại A’ và B’...
Bài 2.9 trang 64 SBT hình học 11
Giải bài 2.9 trang 64 sách bài tập hình học 11. Cho tứ diện S.ABC có D, E lần lượt trung điểm AC, BC và G là trọng tâm tam giác ABC...