Giải SBT toán hình học và đại số giải tích 11 cơ bản Ôn tập chương 1: Phép dời hình và phép đồng dạng trong ..

Bài 1.34 trang 37 SBT hình học 11


Giải bài 1.34 trang 37 sách bài tập hình học 11. Viết phương trình của đường thẳng d1 là ảnh của d qua phép đối xứng qua trục Oy...

Lựa chọn câu để xem lời giải nhanh hơn

Trong mặt phẳng \(Oxy\) cho đường thẳng \(d\) có phương trình \(3x - 2y - 6 = 0\)

LG câu a

Viết phương trình của đường thẳng \({d_1}\) là ảnh của \(d\) qua phép đối xứng qua trục \(Oy\)

Phương pháp giải:

Sử dụng biểu thức tọa độ của phép đối xứng trục \(Oy\): \(\left\{ \begin{array}{l}x' =  - x\\y' = y\end{array} \right.\).

Lời giải chi tiết:

Với mỗi điểm \(M\left( {x;y} \right)\) bất kì thuộc \(d\), gọi \(M'\left( {x';y'} \right) = {D_{Oy}}\left( M \right)\)

Khi đó \(\left\{ \begin{array}{l}x' =  - x\\y' = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - x'\\y = y'\end{array} \right.\).

Mà \(M\left( {x;y} \right) \in d:3x - 2y - 6 = 0\) nên \(3.\left( { - x'} \right) - 2.y' - 6 = 0\) hay \(3x' + 2y' + 6 = 0\).

Vậy \({d_1}:3x + 2y + 6 = 0\).

LG câu b

Viết phương trình của đường thẳng \({d_2}\) là ảnh của \(d\) qua phép đối xứng qua đường thẳng \(\Delta \) có phương trình \(x + y - 2 = 0\). 

Phương pháp giải:

– Tìm giao điểm \(A\) của \(d\) và \(\Delta \).

- Lấy một điểm \(B \in d\), tìm ảnh \(B'\) của \(B\) qua \({D_\Delta }\).

- Viết phương trình \(AB'\) và kết luận.

Lời giải chi tiết:

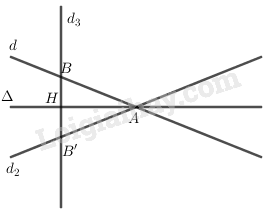
Dễ thấy \(\Delta \) và \(d\) cắt nhau do \(\dfrac{3}{1} \ne \dfrac{{ - 2}}{1}\) nên gọi \(A\left( {x;y} \right) = d \cap \Delta \).

Tọa độ của \(A\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}3x - 2y - 6 = 0\\x + y - 2 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}3x - 2y = 6\\x + y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right.\)

\( \Rightarrow A\left( {2;0} \right)\).

Lấy \(B\left( {0; - 3} \right) \in d\), gọi \(B'\left( {x;y} \right) = {D_\Delta }\left( B \right)\), ta tìm tọa độ \(B'\).

Gọi \({d_3}\) là đường thẳng qua \(B\left( {0; - 3} \right)\) và vuông góc \(\Delta \). Khi đó \(\overrightarrow {{n_{{d_3}}}}  \bot \overrightarrow {{n_d}}  \Rightarrow \overrightarrow {{n_{{d_3}}}}  = \left( {1; - 1} \right)\).

Phương trình \({d_3}:1\left( {x - 0} \right) - 1\left( {y + 3} \right) = 0\) hay \(x - y - 3 = 0\).

Gọi \(H = \Delta  \cap {d_3}\) thì tọa độ của \(H\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}x + y - 2 = 0\\x - y - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{5}{2}\\y =  - \dfrac{1}{2}\end{array} \right.\)

\( \Rightarrow H\left( {\dfrac{5}{2}; - \dfrac{1}{2}} \right)\).

Mà \(B' = {D_\Delta }\left( B \right)\) nên \(H\) là trung điểm của \(BB'\)

\( \Rightarrow \left\{ \begin{array}{l}{x_{B'}} = 2{x_H} - {x_B}\\{y_{B'}} = 2{y_H} - {y_B}\end{array} \right.\)

hay

\(\left\{ \begin{array}{l}{x_{B'}} = 2.\dfrac{5}{2} - 0 = 5\\{y_{B'}} = 2.\left( { - \dfrac{1}{2}} \right) - \left( { - 3} \right) = 2\end{array} \right.\)

\( \Rightarrow B'\left( {5;2} \right)\).

Đường thẳng \({d_2}\) đi qua hai điểm \(A\left( {2;0} \right)\) và \(B'\left( {5;2} \right)\) nên có phương trình \(\dfrac{{x - 2}}{{5 - 2}} = \dfrac{{y - 0}}{{2 - 0}}\) hay \(2x - 3y - 4 = 0\).

Vậy \({d_2}:2x - 3y - 4 = 0\).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Bài 1.35 trang 37 SBT hình học 11

    Giải bài 1.35 trang 37 sách bài tập hình học 11. Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C)...

  • Bài 1.36 trang 37 SBT hình học 11

    Giải bài 1.36 trang 37 sách bài tập hình học 11. Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và r...

  • Bài 1.37 trang 37 SBT hình học 11

    Giải bài 1.37 trang 37 sách bài tập hình học 11. Hãy viết phương trình của đường thẳng d’ là ảnh của d qua phép quay tâm O góc 45°.

  • Bài 1.38 trang 38 SBT hình học 11

    Giải bài 1.38 trang 38 sách bài tập hình học 11. Chứng minh rằng tứ giác MNPQ là một hình thang cân.

  • Bài 1.39 trang 38 SBT hình học 11

    Giải bài 1.39 trang 38 sách bài tập hình học 11. Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng:...

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store