Giải SBT toán hình học và giải tích 12 nâng cao Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số

Bài 1.26 trang 14 SBT Giải tích 12 Nâng cao


Giải bài 1.26 trang 14 sách bài tập Giải tích 12 Nâng cao. Cắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình 1.3) từ một mảnh các tông hình tròn bán kính R

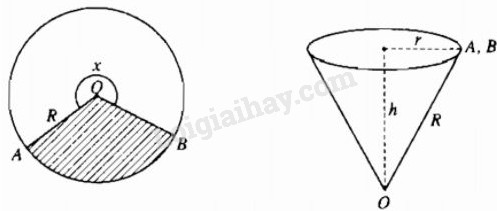
Lựa chọn câu để xem lời giải nhanh hơn

Cắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình 1.3) từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của một hình quạt còn lại với nhau để được một cái phễu có dạng một hình nón. Gọi x là góc ở tâm của hình quạt tròn dùng làm phễu (h.1.3), \(0 < x < 2\pi \)

LG a

Hãy biểu diễn hán kính r của hình tròn đáy và đường cao h của hình nón theo R và x.

Lời giải chi tiết:

Vì độ dài của đường tròn đáy hình nón bằng độ dài \(\overparen{AB}\) của quạt tròn dùng làm phễu, nên ta có \(2\pi r = Rx\)

Do đó \(r = {{Rx} \over {2\pi }}\)

và \(h = \sqrt {{R^2} - {r^2}}  = \sqrt {{R^2} - {{{R^2}{x^2}} \over {4{\pi ^2}}}}  \)\(= {R \over {2\pi }}\sqrt {4{\pi ^2} - {x^2}} \)

LG b

Tính thể tích hình nón theo R và x.

Lời giải chi tiết:

Thể tích hình nón là

\(V = {1 \over 3}\pi {r^2}h = {{{R^3}} \over {24{\pi ^2}}}{x^2}\sqrt {4{\pi ^2} - {x^2}} ,\)\(0 < x < 2\pi \)

LG c

Tìm x để hình nón có thể tích lớn nhất và tính giá trị lớn nhất đó.

Lời giải chi tiết:

Ta tìm \(x \in \left( {0;2\pi } \right)\) sao cho tại đó V đạt giá trị lớn nhất

\(V' = {{{R^3}} \over {24{\pi ^2}}}.{{x\left( {8{\pi ^2} - 3{x^2}} \right)} \over {\sqrt {4{\pi ^2} - {x^2}} }}\)

Với \(0 < x < 2\pi \), ta có

\(V' = 0 \Leftrightarrow 8{\pi ^2} - 3{x^2} = 0 \)

\(\Leftrightarrow x = {{2\sqrt 6 } \over 3}\pi \approx 1,63\pi \)

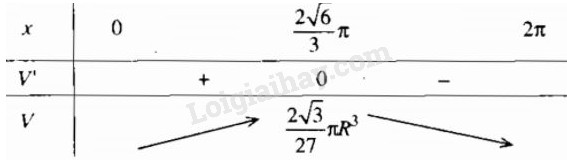
Hình nón có thể tích lớn nhất khi \(x = {{2\sqrt 6\pi } \over 3} \approx 1,63\pi \)

\(\mathop {\max }\limits_{x \in \left( {0;2\pi } \right)} V = V({{2\sqrt 6 \pi} \over 3}) = {{2\sqrt 3 } \over {27}}\pi {R^3}\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store