-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Bài 1.23 trang 14 SBT Giải tích 12 Nâng cao
Giải bài 1.23 trang 14 sách bài tập Giải tích 12 Nâng cao. Hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều dài 1m...
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
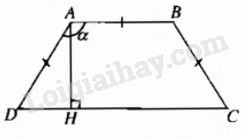
Hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều dài 1m. Tính góc \(\alpha = \widehat {DAB} = \widehat {CBA}\) sao cho hình thang có diện tích lớn nhất và diện tích lớn nhất đó (h.1.1)
Lời giải chi tiết
Dựng \(AH \bot CD\).
Đặt \(x = \widehat {ADC,}0 < x < {\pi \over 2}\) , ta được AH = sinx; DH = cosx; DC = 1+ 2cosx.
Diện tích hình thang là
\(S = {{AB + CD} \over 2}AH \)
\(= (1 + \cos x)\sin x\)
với \(0 < x < {\pi \over 2}\)
Bài toán quy về: Tìm \(x \in \left( {0;{\pi \over 2}} \right)\) sao cho tại điểm đó S đạt giá trị lớn nhất trên khoảng \(\left( {0;{\pi \over 2}} \right)\)
\(\begin{array}{l}S'\left( x \right) = - {\sin ^2}x + \left( {1 + \cos x} \right)\cos x\\ = {\cos ^2}x - 1 + \cos x + {\cos ^2}x\\ = 2{\cos ^2}x + \cos x - 1\\ = \left( {\cos x + 1} \right)\left( {2\cos x - 1} \right)\\S'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\cos x = - 1\\\cos x = \frac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \pi + k2\pi \\x = \pm \frac{\pi }{3} + k2\pi \end{array} \right.\end{array}\)
Mà \(x \in \left( {0;\frac{\pi }{2}} \right)\) nên \(x = \frac{\pi }{3}\).
BBT:
Hình thang có diện tích lớn nhất khi \(\alpha = {{2\pi } \over 3}\) .
Khi đó diện tích hình thang là \(S = {{3\sqrt 3 } \over 4}({m^2})\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.24 trang 14 SBT Giải tích 12 Nâng cao
- Bài 1.25 trang 14 SBT Giải tích 12 Nâng cao
- Bài 1.26 trang 14 SBT Giải tích 12 Nâng cao
- Bài 1.27 trang 15 SBT Giải tích 12 Nâng cao
- Bài 1.28 trang 15 SBT Giải tích 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
