Bài 3.14 trang 139 SBT hình học 11

Giải bài 3.14 trang 139 sách bài tập hình học 11. Chứng minh tứ giác A’B’CD là hình vuông...

Đề bài

Cho hình hộp thoi \(ABCD.A’B’C’D’\) có tất cả các cạnh bằng \(a\) và \(\widehat {ABC} = \widehat {B'BA} = \widehat {B'BC} = {60^0}\). Chứng minh tứ giác \(A’B’CD\) là hình vuông.

Phương pháp giải - Xem chi tiết

Sử dụng dấu hiệu nhận biết: "Hình thoi co một góc vuông là hình vuông".

Lời giải chi tiết

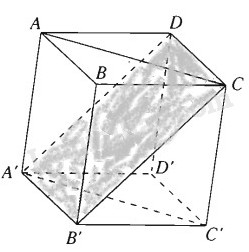
Trước hết dễ thấy tứ giác \(A’B’CD\) là hình bình hành, ngoài ra \(B'C = a = C{\rm{D}}\) nên nó là hình thoi.

Ta chứng minh hình thoi \(A’B’CD\) là hình vuông. Ta có:

\(\eqalign{
& \overrightarrow {CB'} .\overrightarrow {CD} = \left( {\overrightarrow {CB} + \overrightarrow {BB'} } \right).\overrightarrow {BA} \cr
& = \overrightarrow {CB} .\overrightarrow {BA} + \overrightarrow {BB'} .\overrightarrow {BA} \cr
& = - {{{a^2}} \over 2} + {{{a^2}} \over 2} = 0 \cr} \)

Vậy tứ giác \(A’B’CD\) là hình vuông.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 3.15 trang 139 SBT hình học 11
Giải bài 3.15 trang 139 sách bài tập hình học 11. Chứng minh rằng AB và PQ vuông góc với nhau...
Bài 3.13 trang 139 SBT hình học 11
Giải bài 3.13 trang 139 sách bài tập hình học 11. Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau ( hình hộp như vậy còn được gọi là hình hộp thoi). Chứng minh rằng AC ⊥ B’D’
Bài 3.12 trang 139 SBT hình học 11
Giải bài 3.12 trang 139 sách bài tập hình học 11. Chứng minh rằng một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Bài 3.11 trang 139 SBT hình học 11
Giải bài 3.11 trang 139 sách bài tập hình học 11. Tính góc giữa hai đường thẳng AB và SC...
Bài 3.10 trang 138 SBT hình học 11
Giải bài 3.10 trang 138 sách bài tập hình học 11. Cho hình chóp tam giác S.ABC ...
Bài 3.9 trang 138 SBT hình học 11
Giải bài 3.9 trang 138 sách bài tập hình học 11. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, AD và có MN = PQ . Chứng minh rằng AB ⊥ CD...
Bài 3.8 trang 138 SBT hình học 11
Giải bài 3.8 trang 138 sách bài tập hình học 11. Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC...