Giải SBT toán hình học và đại số 11 nâng cao Ôn tập chương III. Vectơ trong không gian. Quan hệ vuôn..

Câu 82 trang 130 Sách bài tập Hình học 11 Nâng cao


Giải bài tập Câu 82 trang 130 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Lấy điểm M thuộc đoạn thẳng AD’, điểm N thuộc đoạn thẳng BD sao cho

\(AM = DN = x\left( {0 < x < a\sqrt 2 } \right)\)

a) Tìm x để đoạn thẳng MN có độ dài ngắn nhất.

b) Khi MN ngắn nhất, hãy chứng tỏ MN là đường vuông góc chung của AD’ và DB, đồng thời MN // A’C.

Lời giải chi tiết

 

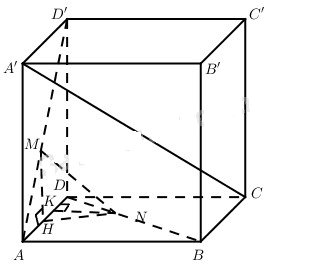
a) Kẻ \(MH \bot A{\rm{D}}\) thì \(MH \bot \left( {ABC{\rm{D}}} \right)\) và \(MH = {{x\sqrt 2 } \over 2} = AH\).

Kẻ \(NK \bot A{\rm{D}}\) thì \(NK = {{x\sqrt 2 } \over 2} = DK\).

Vậy \(KH = \left| {a - x\sqrt 2 } \right|\).

Ta có:

\(\eqalign{  & M{N^2} = M{H^2} + H{K^2} + K{N^2}  \cr  &  = 3{{\rm{x}}^2} - 2a\sqrt 2 x + ah2 \cr} \)

Từ đó MN nhỏ nhất khi và chỉ khi \(x = {{a\sqrt 2 } \over 3}\).

b) Khi \(x = {{a\sqrt 2 } \over 3}\) thì

\(\eqalign{  & M{N^2} = {{3{{\rm{a}}^2}} \over 9} = {{{a^2}} \over 3};  \cr  & A{M^2} = {{2{{\rm{a}}^2}} \over 9};  \cr  & A{N^2} = A{{\rm{D}}^2} + D{N^2} - 2{\rm{AD}}{\rm{.DNcos4}}{{\rm{5}}^0} = {{5{a^2}} \over 9} \cr} \)

Từ đó \(A{N^2} = A{M^2} + M{N^2}\) hay \(MN \bot A{\rm{D}}'\).

Chứng minh tương tự như trên, ta cũng có \(MN \bot B{\rm{D}}\).

Vậy MN là đường vuông góc chung của AD’ và BD.

Khi \(DN = {{a\sqrt 2 } \over 3}\) thì NB = 2ND.

Gọi I là trung điểm của AD thì ta có I, N, C thẳng hàng

 

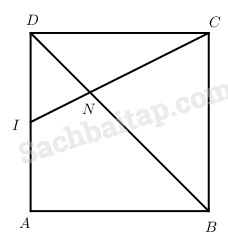
Tương tự ta cũng có các điểm I, M, A’ thẳng hàng.

Xét tam giác A’IC ta có:

\({{IN} \over {NC}} = {{IM} \over {MA'}} = {1 \over 2}\)

Vậy MN // A’C.

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store