Câu 74 trang 128 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho tứ diện ABCD. Gọi \({A_1},{B_1},{C_1},{D_1}\) là các điểm lần lượt thuộc các đường thẳng AB, BC, CD, DA sao cho \(\overrightarrow {{A_1}A}  = k\overrightarrow {{A_1}B} ,\overrightarrow {{B_1}B}  = k\overrightarrow {{B_1}C} \) , \(\overrightarrow {{C_1}C}  = k\overrightarrow {{C_1}D} ,\overrightarrow {{D_1}D}  = k\overrightarrow {{D_1}A} \). Với giá trị bào của k thì bốn điểm \({A_1},{B_1},{C_1},{D_1}\) cùng thuộc một mặt phẳng?

Lời giải chi tiết

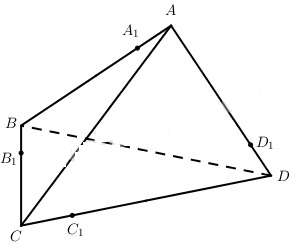
Cách 1. 

Đặt \(\overrightarrow {DA}  = \overrightarrow a ,\overrightarrow {DB}  = \overrightarrow b ,\overrightarrow {DC}  = \overrightarrow c \) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng.

Các điểm \({A_1},{B_1},{C_1},{D_1}\)  cùng thuộc một mặt phẳng khi và chỉ khi có các số m, n để

\(\overrightarrow {{D_1}{B_1}}  = m\overrightarrow {{D_1}{A_1}}  + n\overrightarrow {{D_1}{C_1}} \,\,\,\,\,\,\,\,\,\left( 1 \right)\)

Từ hệ thức \(\overrightarrow {{B_1}B}  = k\overrightarrow {{B_1}C} \), ta có

\(\overrightarrow {{D_1}{B_1}}  = {{\overrightarrow {{D_1}B}  - k\overrightarrow {{D_1}C} } \over {1 - k}}\)

hay

\(\eqalign{  & \overrightarrow {{D_1}{B_1}}  = {{\overrightarrow {{D_1}D}  + \overrightarrow {DB}  - k\left( {\overrightarrow {{D_1}D}  + \overrightarrow {DC} } \right)} \over {1 - k}}  \cr  &  = \overrightarrow {{D_1}D}  + {1 \over {1 - k}}\overrightarrow b  - {k \over {1 - k}}\overrightarrow c  \cr} \)

Mặt khác

 \(\eqalign{  & \overrightarrow {{D_1}D}  = k\overrightarrow {{D_1}A}  = k\left( {\overrightarrow {{D_1}D}  + \overrightarrow {DA} } \right)  \cr  &  \Rightarrow \overrightarrow {{D_1}D}  = {k \over {1 - k}}\overrightarrow a  \cr} \)

Vậy \(\overrightarrow {{D_1}{B_1}}  = {k \over {1 - k}}\overrightarrow a  + {1 \over {1 - k}}\overrightarrow b  - {k \over {1 - k}}\overrightarrow c \).

Tương tự như trên, ta có

\(\eqalign{  & \overrightarrow {{D_1}{A_1}}  = {{\overrightarrow {{D_1}A}  - k\overrightarrow {{D_1}B} } \over {1 - k}}  \cr  &  = {{\overrightarrow {{D_1}D}  + \overrightarrow {DA}  - k\left( {\overrightarrow {{D_1}D}  + \overrightarrow {DB} } \right)} \over {1 - k}}  \cr  &  = \overrightarrow {{D_1}D}  + {1 \over {1 - k}}\overrightarrow a  - {k \over {1 - k}}\overrightarrow b  \cr} \)

hay

\(\eqalign{  & \overrightarrow {{D_1}{A_1}}  = {{k + 1} \over {1 - k}}\overrightarrow a  - {k \over {1 - k}}\overrightarrow b \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)  \cr  & \overrightarrow {{D_1}{C_1}}  = {{\overrightarrow {{D_1}C}  - k\overrightarrow {{D_1}D} } \over {1 - k}}  \cr  &  = {{\overrightarrow {{D_1}D}  + \overrightarrow {DC}  - k\overrightarrow {{D_1}D} } \over {1 - k}}  \cr  &  = \overrightarrow {{D_1}D}  + {1 \over {1 - k}}\overrightarrow c  \cr} \)

do đó \(\overrightarrow {{D_1}{C_1}}  = {k \over {1 - k}}\overrightarrow a  + {1 \over {1 - k}}\overrightarrow c .\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\)

Từ (1), (2), (3), (4) ta có các điểm \({A_1},{B_1},{C_1},{D_1}\) cùng thuộc mặt phẳng khi và chỉ khi

\(k\overrightarrow a  + \overrightarrow b  - k\overrightarrow c \)

\(= \left( {mk + nk + m} \right)\overrightarrow a  - mk\overrightarrow b  + n\overrightarrow c \)

Do \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng nên đẳng thức trên xảy ra khi và chỉ khi có các số m, n để

\(\left\{ \matrix{  k = mk + nk + m \hfill \cr  1 =  - mk \hfill \cr   - k = n \hfill \cr}  \right.\)

Điều đó tương đương với \(k =  - 1 - {k^2} - {1 \over k}\) hay \({k^3} + {k^2} + k + 1 = 0\) hay k = -1.

Vậy với k = -1 thì các điểm \({A_1},{B_1},{C_1},{D_1}\) cùng thuộc một mặt phẳng.

Cách 2.

Đặt \(\overrightarrow {DA}  = \overrightarrow a ,\overrightarrow {DB}  = \overrightarrow b ,\overrightarrow {DC}  = \overrightarrow c \). Tìm k để các điểm \({A_1},{B_1},{C_1},{D_1}\) cùng thuộc một mặt phẳng tương đương với việc tìm k để có biểu diễn

\(\overrightarrow {D{A_1}}  = x\overrightarrow {D{B_1}}  + y\overrightarrow {D{C_1}}  + z\overrightarrow {{\rm{D}}{{\rm{D}}_1}} \) 

với x + y + z = 1               (a)

Từ hệ thức \(\overrightarrow {{A_1}A}  = k\overrightarrow {{A_1}B} \) ta có

\(\eqalign{  & \overrightarrow {D{A_1}}  = {{\overrightarrow {DA}  - k\overrightarrow {DB} } \over {1 - k}}  \cr  &  = {1 \over {1 - k}}\overrightarrow a  - {k \over {1 - k}}\overrightarrow b \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr} \)

Tương tự như trên, ta cũng có

\(\overrightarrow {D{B_1}}  = {1 \over {1 - k}}\overrightarrow b  - {k \over {1 - k}}\overrightarrow c \,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)

Mặt khác từ \(\overrightarrow {{C_1}C}  = k\overrightarrow {{C_1}D} \) ta có

\(\eqalign{  & \overrightarrow {{C_1}D}  + \overrightarrow {DC}  = k\overrightarrow {{C_1}D}   \cr  &  \Leftrightarrow \overrightarrow {D{C_1}}  = {1 \over {1 - k}}\overrightarrow c \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right) \cr} \)

Tương tự từ \(\overrightarrow {{D_1}D}  = k\overrightarrow {{D_1}A} \), ta cũng có

\(\overrightarrow {{D_1}D}  = {k \over {1 - k}}\overrightarrow a \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\)

Từ (1), (2), (3), (4), ta suy ra

\(\overrightarrow {D{A_1}}  =  - {1 \over k}\overrightarrow {{\rm{D}}{{\rm{D}}_1}}  - k\overrightarrow {D{B_1}}  - {k^2}\overrightarrow {D{C_1}} \,\,\,\,\,\,\,\,\,\,\,\left( b \right)\)

Từ (a) và (b) ta có các điểm \({A_1},{B_1},{C_1},{D_1}\) cùng thuộc một mặt phẳng khi và chỉ khi:

\(\eqalign{  &  - {1 \over k} - k - {k^2} = 1  \cr  &  \Leftrightarrow {k^3} + {k^2} + k + 1 = 0  \cr  &  \Leftrightarrow k =  - 1 \cr} \)

Vậy với k = -1 thì các điểm \({A_1},{B_1},{C_1},{D_1}\) cùng thuộc một mặt phẳng.

Loigiaihay.com