-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Bài 4 trang 143 SGK Giải tích 12
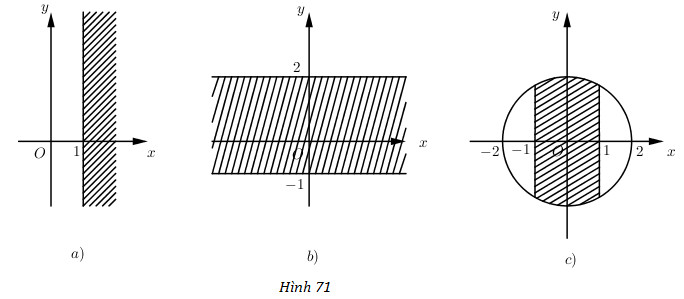
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình a), b), c) sau:
Đề bài
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình 71 a), b), c) ?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi số phức có dạng \(z=x+yi\), (\(x,y \in R\)), khi đó số phức \(z\) được biểu diễn bởi điểm \(M(x, y)\) trên mặt phẳng tọa độ \(Oxy\).
Tìm miền giá trị của \(x,y\) ở từng ý và nhận xét về số phức \(z\).
Lời giải chi tiết
Giả sử \(z = x + yi\) (\(x,y \in \mathbb R\)), khi đó số phức \(z\) được biểu diễn bởi điểm \(M(x, y)\) trên mặt phẳng tọa độ \(Oxy\).
a) Tập hợp điểm M biểu diễn cho số phức \(z\) thuộc phần gạch chéo là \(\left\{ {M\left( {x;y} \right)|x \ge 1} \right\}\).
Vậy số phức thỏa mãn là \(z=x+yi\) với \(x\ge 1\).
b) Tập hợp điểm M biểu diễn cho số phức \(z\) thuộc phần gạch chéo là \(\left\{ {M\left( {x;y} \right)| - 1 \le y \le 2} \right\}\)
Vậy số phức thỏa mãn là \(z=x+yi\) với \(-1\le y\le 2\).
c) Tập hợp điểm M biểu diễn cho số phức \(z\) thuộc phần gạch chéo là \(\left\{ {M\left( {x;y} \right)|{x^2} + {y^2} = 4, - 1 \le x \le 1} \right\}\).
Vậy số phức cần tìm có phần thực thuộc đoạn \([-1, 1]\) và môdun không vượt quá \(2\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 5 trang 143 SGK Giải tích 12
- Bài 6 trang 143 SGK Giải tích 12
- Bài 7 trang 143 SGK Giải tích 12
- Bài 8 trang 143 SGK Giải tích 12
- Bài 9 trang 144 SGK Giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
