-
ĐẠI SỐ - SBT TOÁN 10 NÂNG CAO
-
Chương 1: Mệnh đề - Tập hợp
-
Chương 2: Hàm số
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT VÀ BẬC HAI
- Bài 1. Đại cương về phương trình
- Bài 2. Phương trình bậc nhất và bậc hai một ẩn
- Bài 3. Một số phương trình quy về phương trình bậc nhất hoặc bậc hai
- Bài 4. Phương trình và hệ phương trình bậc nhất nhiều ẩn
- Bài 5. Một số ví dụ về hệ phương trình bậc hai hai ẩn
- Bài tập Ôn tập chương III - Phương trình bậc nhất và bậc hai
-
CHƯƠNG IV. BẤT ĐẲNG THỨC VÀ BẤT PHƯƠNG TRÌNH
- Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
- Bài 2. Đại cương về bất phương trình
- Bài 3. Bất phương trình và hệ bất phương trình bậc nhất một ẩn
- Bài 4. Dấu của nhị thức bậc nhất
- Bài 5. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
- Bài 6. Dấu của tam thức bậc hai
- Bài 7. Bất phương trình bậc hai
- Bài 8. Một số phương trình và bất phương trình quy về bậc hai
- Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
-
CHƯƠNG V. THỐNG KÊ
-
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
-
BÀI TẬP ÔN TẬP CUỐI NĂM - ĐẠI SỐ 10 NÂNG CAO
-
-
HÌNH HỌC-SBT TOÁN 10 NÂNG CAO
Bài 37 trang 11 SBT Hình học 10 Nâng cao
Giải bài 37 trang 11 sách bài tập Hình học 10 Nâng cao. Cho tam giác ABC với các cạnh AB=c, BC=a, CA=b...
Đề bài
Cho tam giác \(ABC\) với các cạnh \(AB=c, BC=a, CA=b.\)
a) Gọi \(CM\) là đường phân giác trong của góc \(C\). Hãy biểu thị vec tơ \(\overrightarrow {CM} \) theo các vec tơ \(\overrightarrow {CA} \) và \(\overrightarrow {CB} \).
b) Gọi \(I\) là tâm đường tròn nội tiếp tam giác \(ABC\). Chứng minh rằng
\(a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} = \overrightarrow 0 \).
Lời giải chi tiết
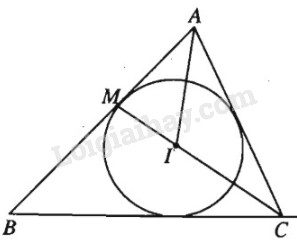
a) Theo tính chất đường phân giác , ta có
\(\dfrac{{AM}}{{BM}} = \dfrac{{CA}}{{CB}} = \dfrac{b}{a}\), suy ra \(\overrightarrow {MA} = - \dfrac{b}{a}\overrightarrow {MB} \).
Từ đó , ta có \(\overrightarrow {CM} = \dfrac{{\overrightarrow {CA} + \dfrac{b}{a}\overrightarrow {CB} }}{{1 + \dfrac{b}{a}}}\)
\(= \dfrac{a}{{a + b}}\overrightarrow {CA} + \dfrac{b}{{a + b}}\overrightarrow {CB} .\)
b) Vì \(I\) là tâm đường tròn nội tiếp tam giác \(ABC\) nên \(AI\) là phân giác của tam giác \(ACM\). Bởi vậy theo câu a), ta có biểu thị vec tơ \(\overrightarrow {AI} \) theo hai vec tơ \(\overrightarrow {AM} \) và \(\overrightarrow {AC} \).
\(\begin{array}{l}\overrightarrow {AI} = \dfrac{{AC}}{{AC + AM}}\overrightarrow {AM} + \dfrac{{AM}}{{AC + AM}}\overrightarrow {AC}\\ = \dfrac{b}{{b + \dfrac{{bc}}{{a + b}}}}.\dfrac{b}{{a + b}}\overrightarrow {AB} + \dfrac{{\dfrac{{bc}}{{a + b}}}}{{b + \dfrac{{bc}}{{a + b}}}}\overrightarrow {AC} \\ = \dfrac{b}{{a + b + c}}\overrightarrow {AB} + \dfrac{c}{{a + b + c}}\overrightarrow {AC}\\ = \dfrac{b}{{a + b + c}}(\overrightarrow {IB} - \overrightarrow {IA} ) + \dfrac{c}{{a + b + c}}(\overrightarrow {IC} - \overrightarrow {IA} ).\end{array}\)
Suy ra
\(\left( {1 - \dfrac{{b + c}}{{a + b + c}}} \right)\overrightarrow {IA} + \dfrac{b}{{a + b + c}}\overrightarrow {IB} + \dfrac{c}{{a + b + c}}\overrightarrow {IC} = \overrightarrow 0 \\ \Leftrightarrow \,\,\,a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} = \overrightarrow 0 .\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 38 trang 11 SBT Hình học 10 Nâng cao
- Bài 39 trang 11 SBT Hình học 10 Nâng cao
- Bài 40 trang 11 SBT Hình học 10 Nâng cao
- Bài 41 trang 11 SBT Hình học 10 Nâng cao
- Bài 42 trang 12 SBT Hình học 10 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
