-
ĐẠI SỐ VÀ GIẢI TÍCH- SBT TOÁN 11
-
HÌNH HỌC SBT - TOÁN 11
-
Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
- Bài 1+Bài 2: Phép biến hình. Phép tịnh tiến
- Bài 3: Phép đối xứng trục
- Bài 4: Phép đối xứng tâm
- Bài 5: Phép quay
- Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Bài 7: Phép vị tự
- Bài 8: Phép đồng dạng
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Câu hỏi và bài tập
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Đề toán tổng hợp
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Câu hỏi trắc nghiệm
-
Chương 2: Đường thẳng và mặt phẳng trong không gian quan hệ song song
- Bài 1: Đại cương về đường thằng và mặt phẳng
- Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3: Đường thẳng và mặt phẳng song song
- Bài 4: Hai mặt phẳng song song
- Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Câu hỏi và bài tập
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Đề toán tổng hợp
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Câu hỏi trắc nghiệm
-
Chương 3: Vecto trong không gian. Quan hệ vuông góc trong không gian
-
Ôn tập cuối năm Hình học 11
-
Giải SBT toán hình học và đại số giải tích 11 cơ bản
Ôn tập chương 2: Đường thẳng và mặt phẳng trong không g..
Bài 2.50 trang 84 SBT hình học 11
Giải bài 2.50 trang 84 sách bài tập hình học 11. Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho:...
Đề bài
Cho tứ diện \(ABCD\). Tìm vị trí điểm \(M\) trong không gian sao cho: \(M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị cực tiểu.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất:
Cho \(I\) là trung điểm đoạn thẳng \(AB\). Với điểm \(M\) bất kì ta luôn có:
\(MA^2+MB^2=2MI^2+\dfrac{1}{2}AB^2\)
Lời giải chi tiết
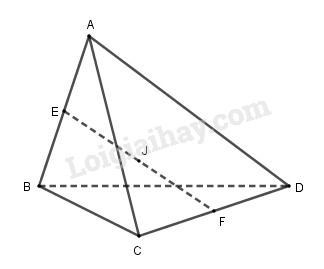
Gọi \(\displaystyle E, F\) lần lượt là trung điểm của \(\displaystyle AB\) và \(\displaystyle CD\). Ta có:
\(\begin{array}{l}
M{A^2} + M{B^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2}\\
= {\left( {\overrightarrow {ME} + \overrightarrow {EA} } \right)^2} + {\left( {\overrightarrow {ME} + \overrightarrow {EB} } \right)^2}\\
= {\overrightarrow {ME} ^2} + 2\overrightarrow {ME} .\overrightarrow {EA} + {\overrightarrow {EA} ^2}\\
+ {\overrightarrow {ME} ^2} + 2\overrightarrow {ME} .\overrightarrow {EB} + {\overrightarrow {EB} ^2}\\
= 2M{E^2} + 2\overrightarrow {ME} \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + E{A^2} + E{B^2}\\
= 2M{E^2} + 0 + \frac{1}{4}A{B^2} + \frac{1}{4}A{B^2}\\
= 2M{E^2} + \frac{1}{2}A{B^2}
\end{array}\)
Do đó, \(\displaystyle M{A^2} + M{B^2} = 2M{E^2} + {1 \over 2}A{B^2}\,\,\,\,\,\left( 1 \right)\)
\(\displaystyle M{C^2} + M{D^2} = 2M{F^2} + {1 \over 2}C{{\rm{D}}^2}\,\,\,\,\,\left( 2 \right)\)
Cộng (1) và (2) ta có:
\(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\)
\(\displaystyle = 2\left( {M{E^2} + M{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}\,\,} \right)\,\,\)
Gọi \(\displaystyle J\) là trung điểm của \(\displaystyle EF\), ta có:
\(\displaystyle \left( {M{E^2} + M{F^2}} \right) = 2M{J^2}\, + {1 \over 2}E{F^2}\)
Khi đó:
\(\displaystyle \eqalign{
& M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2} \cr
& = 2\left( {2M{J^2}\, + {1 \over 2}E{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr
& = 4M{J^2} + E{F^2} + \frac{1}{2}\left( {A{B^2} + C{D^2}} \right)\cr &\ge E{F^2} + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr} \)
Vậy \(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị nhỏ nhất khi \(MJ = 0\) hay \(\displaystyle M \equiv J\).
Loigiaihay.com
Bình luận
Chia sẻ- Bài 2.49 trang 83 SBT hình học 11
- Bài 2.48 trang 83 SBT hình học 11
- Bài 2.47 trang 83 SBT hình học 11
- Bài 2.46 trang 83 SBT hình học 11
- Bài 2.45 trang 83 SBT hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
