Giải SBT toán hình học và đại số giải tích 11 cơ bản Ôn tập chương 2: Đường thẳng và mặt phẳng trong không g..

Bài 2.47 trang 83 SBT hình học 11


Giải bài 2.47 trang 83 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là hình thang ABCD (có đáy nhỏ BC). Gọi M, N lần lượt là trung điểm của AB và SD, O là giao điểm của AC và DM...

Đề bài

Cho hình chóp \(S.ABCD \) có đáy là hình thang \(ABCD \) (có đáy nhỏ \(BC\)). Gọi \(M, N\) lần lượt là trung điểm của \(AB \) và \(SD, O \) là giao điểm của \(AC \) và \(DM\).

a) Tìm giao điểm của \(MN\) và mặt phẳng \((SAC)\) .

b) Tìm thiết diện của hình chóp với mặt phẳng \((NBC)\). Thiết diện đó là hình gì?

Phương pháp giải - Xem chi tiết

a) Tìm mặt phẳng chứa \(MN\) và cắt \((SAC)\).

Tìm giao tuyến của \((SAC)\) với mặt phẳng vừa tìm.

Tìm giao điểm của \(MN\) với giao tuyến trên và kết luận.

b) Tìm giao tuyến của \((NBC)\) với các mặt của hình chóp (nếu có).

Lời giải chi tiết

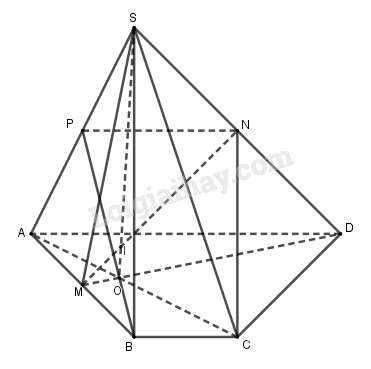
a) Gọi \(O = AC \cap MD\).

Ta có: \(\left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in MD \subset \left( {SMD} \right)\end{array} \right.\) \( \Rightarrow O \in \left( {SAC} \right) \cap \left( {SMD} \right)\)

Mà \(S \in \left( {SAC} \right) \cap \left( {SMD} \right)\)

\( \Rightarrow SO = \left( {SAC} \right) \cap \left( {SMD} \right)\)

Trong mặt phẳng \((SMB) \) gọi \(I = SO \cap MN\).

Ta có:

\(\left\{ \begin{array}{l}
I \in MN\\
I \in SO \subset \left( {SAC} \right)
\end{array} \right.  \)

\(\Rightarrow I = \left( {SAC} \right) \cap MN\)

b) \(A{\rm{D}}\parallel BC\left( {BC \subset \left( {SBC} \right)} \right)\)

\( \Rightarrow A{\rm{D}}\parallel \left( {SBC} \right)\).

Mặt phẳng \((SAD) \) cắt mặt phẳng \((NBC) \) theo giao tuyến \(NP\parallel A{\rm{D}}\left( {P \in SA} \right)\).

Ta có thiết diện cần tìm là hình thang \(BCNP\).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Bài 2.48 trang 83 SBT hình học 11

    Giải bài 2.48 trang 83 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi G1 và G1 lần lượt là trọng tâm của các tam giác SBC và SCD...

  • Bài 2.49 trang 83 SBT hình học 11

    Giải bài 2.49 trang 83 sách bài tập hình học 11. Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B’, C’, D’ sao cho đường thẳng B’C’cắt đường thẳng BC tại K, đường thẳng C’D’ cắt đường thẳng CD tại J, đường thẳng D’B’ cắt đường thẳng DB tại I...

  • Bài 2.50 trang 84 SBT hình học 11

    Giải bài 2.50 trang 84 sách bài tập hình học 11. Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho:...

  • Bài 2.46 trang 83 SBT hình học 11

    Giải bài 2.46 trang 83 sách bài tập hình học 11. Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi C’ là trung điểm của SC và M là một điểm di động trên cạnh SA. Mặt phẳng (P) di động luôn đi qua C’M và song song với BC...

  • Bài 2.45 trang 83 SBT hình học 11

    Giải bài 2.45 trang 83 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là hình thang ( đáy lớn AD). Gọi O la giao điểm của AC và BD, I và J lần lượt là trung điểm của SB và SC...

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua