Trả lời câu hỏi 5 trang 16 SGK Giải tích 12

Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau:

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số: \(f(x) = \,x({x^2} - 3)\)

Video hướng dẫn giải

Lời giải chi tiết

1. TXĐ: \(D = \mathbb R\)

2. \(f\left( x \right) = 3{x^2}-3\). Cho \(f\left( x \right) = 0{\rm{ }} \Leftrightarrow {\rm{ }}x = 1\) hoặc \(x = -1.\)

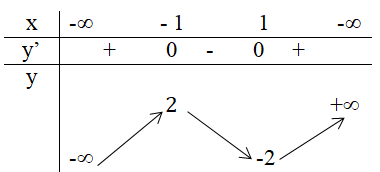
3. Ta có bảng biến thiên:

Hàm số đạt cực đại tại \(x = -1\) và giá trị cực đại là \(2\)

Hàm số đạt cực tiểu tại \(x = 1\) và giá trị cực tiểu là \(-2.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 7 phiếu

Bài tiếp theo

Giải bài 1 trang 18 SGK Giải tích 12
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau:
Giải bài 2 trang 18 SGK Giải tích 12
Áp dụng quy tắc II, hãy tìm các điểm cực trị của hàm số sau:
Giải bài 3 trang 18 SGK Giải tích 12
Chứng minh rằng
Giải bài 4 trang 18 SGK Giải tích 12
Chứng minh rằng với mọi giá trị của tham số m, hàm số:
Giải bài 5 trang 18 SGK Giải tích 12
Tìm a và b để các cực trị của hàm số:
Giải bài 6 trang 18 SGK Giải tích 12
Xác định giá trị của tham số m
Các dạng toán về cực trị có tham số đối với các hàm số đơn giản
Một số dạng toán
Trả lời câu hỏi 4 trang 16 SGK Giải tích 12
Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không ?...
Trả lời câu hỏi 3 trang 14 SGK Giải tích 12
Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không....
Trả lời câu hỏi 2 trang 14 SGK Giải tích 12
Giả sử f(x) đạt cực đại tại xo. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số...
Trả lời câu hỏi 1 trang 13 SGK Giải tích 12
Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất)...
Lý thuyết cực trị của hàm số
Cho hàm số y = f(x) liên tục trên khoảng (a ; b) và điểm x ∈ (a ; b).