-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Trả lời câu hỏi 3 trang 14 SGK Giải tích 12
Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không....
Video hướng dẫn giải
a) Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không
\(y = -2x + 1;\)
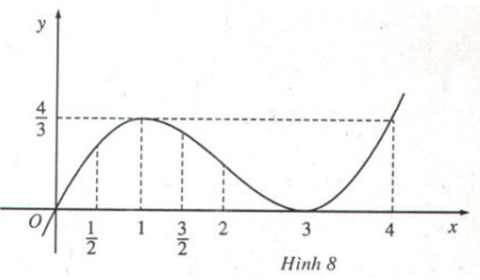
\(y = \dfrac {x{{(x - 3)}^2}} 3\,\,\,(H.8)\)
b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
LG a
Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không
\(y = -2x + 1;\)
\(y = \dfrac {x{{(x - 3)}^2}} 3\,\,\,(H.8)\)
Phương pháp giải:
Quan sát đồ thị, tìm điểm cực trị ( cực đại: điểm mà tại đó hàm số chuyển từ đồng biến sang nghịch biến, cực tiểu: ngược lại)
Lời giải chi tiết:
Hàm số \(y = -2x + 1\) không có cực trị.
Hàm số \(y = \dfrac {x{{(x - 3)}^2}} 3\) đạt cực đại tại \(x = 1\) và đạt cực tiểu tại \(x = 3.\)
LG b
Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
Lời giải chi tiết:
Nếu hàm số có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
Loigiaihay.com
Bình luận
Chia sẻ
- Trả lời câu hỏi 4 trang 16 SGK Giải tích 12
- Trả lời câu hỏi 5 trang 16 SGK Giải tích 12
- Giải bài 1 trang 18 SGK Giải tích 12
- Giải bài 2 trang 18 SGK Giải tích 12
- Giải bài 3 trang 18 SGK Giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
