Câu 45 trang 59 Sách Bài tập Hình học 11 Nâng cao

Cho hình chóp S.ABCD. Các điểm I, J, K lần lượt là trọng tâm các tam giác SAB, SBC, SCA.

Đề bài

Cho hình chóp S.ABCD. Các điểm I, J, K lần lượt là trọng tâm các tam giác SAB, SBC, SCA.

a) Chứng minh rằng (IJK) // (ABC).

b) Tìm tập hợp các điểm M nằm trong hình chóp S.ABC sao cho KM song song với mp(ABC).

Lời giải chi tiết

(h.98)

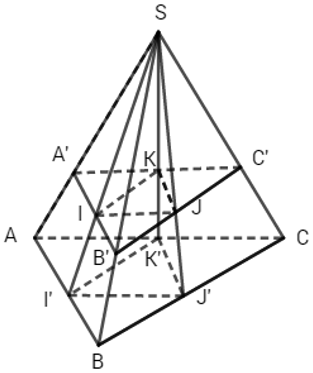
a) Gọi I’, J’, K’ lần lượt là giao điểm của các cặp đường thẳng SI và AB, SJ và BC, SK và CA. Khi đó I’, J’, K’ lần lượt là trung điểm của các cạnh AB, BC và CA.

Ta có: \({{SI} \over {SI'}} = {{SK} \over {SK'}} = {{SJ} \over {SJ'}} = {2 \over 3}\)

\( \Rightarrow \) IK // I’K’, KJ // K’J’

\( \Rightarrow \) mp(IJK) // mp(I’J’K’).

Mặt khác mp(I’J’K’) \( \equiv \) mp(ABC)

Vậy (IJK) // (ABC)

b) Ta có KM // (ABC) khi và chỉ khi KM thuộc mp(P) qua K và song song với mp(ABC). Vậy KM // (ABC) khi và chỉ khi M \( \in \) (P).

Gọi A’, B’, C’ lần lượt là các giao điểm của (P) với các cạnh SA, SB, SC. Khi đó A’B’ // AB,B’C’ // BC, C’A’ // CA.

Theo giả thiết M chỉ nằm trong hình chóp S.ABCD, nên tập hợp các điểm M sao cho KM // (ABC) là tam giác A’B’C’.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Câu 46 trang 59 Sách Bài tập Hình học 11 Nâng cao
Cho hình chóp S.ABCD đáy là hình thang (AB // CD). Điểm M thuộc cạnh BC không trùng với B và C.
Câu 47 trang 59 - 60 Sách Bài tập Hình học 11 Nâng cao
Cho tứ diện ABCD. Gọi I và J lần lượt là trung điểm của AB và CD. Một mặt phẳng IJ cắt các cạnh AD và BC lần lượt tại N và M.
Câu 48 trang 60 Sách Bài tập Hình học 11 Nâng cao
Cho tứ diện ABCD. Hai điểm M, N lần lượt thay đổi trên hai cạnh AB và CD. Tìm tập hợp trung điểm I của MN.
Câu 49 trang 60 Sách Bài tập Hình học 11 Nâng cao
Hãy dùng định lí Ta-lét để giải bài tập 31 (chương II).
Câu 50 trang 60 Sách Bài tập Hình học 11 Nâng cao
Cho tứ diện ABCD. Hãy dựng một hình hộp ngoại tiếp tứ diện đó (tức là dựng một hình hộp sao cho mỗi cạnh của tứ diện đều là đường chéo của một mặt của hình hộp).
Câu 51 trang 60 Sách Bài tập Hình học 11 Nâng cao
Cho hình hộp ABCD.A’B’C’D’ có tất cả các mặt bên đều là hình vuông cạnh bằng a.
Câu 52 trang 60 Sách Bài tập Hình học 11 Nâng cao
Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng (P) qua điểm K và song song với mặt phẳng (EAC).
Câu 53 trang 60 Sách Bài tập Hình học 11 Nâng cao
Cho lăng trụ tam giác ABC.A’B’C’.
Câu 54 trang 60 - 61 Sách Bài tập Hình học 11 Nâng cao
Cho lăng trụ tam giác ABC.A’B’C’. Gọi I, J, K lần lượt là tâm của các hình bình hành ACC’A’, BCC’B’, ABB’A’.
Câu 55 trang 61 Sách Bài tập Hình học 11 Nâng cao
Cho hình hộp ABCD.A’B’C’D’. Điểm M thuộc cạnh AD, điểm N thuộc cạnh D’C’ sao cho AM : MD = D’N : NC’.
Câu 56 trang 61 Sách Bài tập Hình học 11 Nâng cao
Cho hình hộp ABCD.A’B’C’D’. Gọi P, Q, R, S lần lượt là tâm các mặt bên ABB’A’, BCC’B’, CDD’C’, DAA’D’.
Câu 57 trang 61 Sách Bài tập Hình học 11 Nâng cao
Cho hình chóp cụt tứ giác ABCD.A’B’C’D’, có các cạnh bên là AA’, BB’, CC’, DD’ và có đáy lớn ABCD là hình bình hành.
Câu 44 trang 59 Sách Bài tập Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) cắt các cạnh bên SA, SB, SC, SD lần lượt tại A’, B’, C’, D’.
Câu 43 trang 59 Sách Bài tập Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là một tứ giác lồi. M là trung điểm của cạnh bên SA, N là trung điểm của cạnh bên SC.
Câu 42 trang 59 Sách Bài tập Hình học 11 Nâng cao
Cho một mặt phẳng (P) và một điểm A nằm ngoài (P). Chứng minh rằng tất cả những đường thẳng đi qua A và song song với (P) đều nằm cùng trong một mặt phẳng (Q) song song với (P).
Câu 41 trang 59 Sách Bài tập Hình học 11 Nâng cao
Cho hai mặt phẳng song song (P) và (Q); hai đường thẳng song song a và b.
Câu 40 trang 58 – 59 Sách Bài tập Hình học 11 Nâng cao
Trong các mệnh đề sau, mệnh đề nào đúng?