Câu 42 trang 59 Sách Bài tập Hình học 11 Nâng cao
Cho một mặt phẳng (P) và một điểm A nằm ngoài (P). Chứng minh rằng tất cả những đường thẳng đi qua A và song song với (P) đều nằm cùng trong một mặt phẳng (Q) song song với (P).
Đề bài
Cho một mặt phẳng (P) và một điểm A nằm ngoài (P). Chứng minh rằng tất cả những đường thẳng đi qua A và song song với (P) đều nằm cùng trong một mặt phẳng (Q) song song với (P).
Lời giải chi tiết
(h.95)
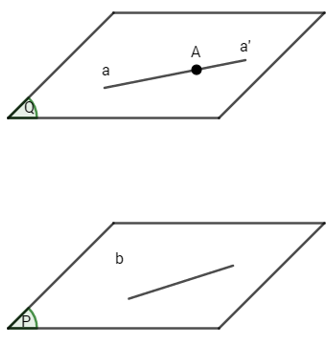
Gọi (Q) là mặt phẳng duy nhất đi qua A và song song với (P). Giả sử a là một đường thẳng bất kì qua A và song song với (P). Ta phải chứng minh đường thẳng a nằm trên (Q).
Vì a// (P) nên có đường thẳng b thuộc (P) sao cho a và b song song. Vậy mp(a, b) cắt (Q) theo giao tuyến a’ qua A và song song với b. Từ đó a trùng với a’, tức là a nằm trên (Q).
Loigiaihay.com
Các bài khác cùng chuyên mục













Danh sách bình luận