Bài 22 trang 199 Sách bài tập (SBT) Toán Hình học 10
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có \({x_A} = 2\), điểm C và trung điểm K của AD cùng thuộc trục Oy, tâm I thuộc trục Ox, AD = 2AB. Tìm tọa độ các đỉnh của hình chữ nhật ABCD, biết rằng K có tung độ âm.
Gợi ý làm bài
(Xem hình 3.45)
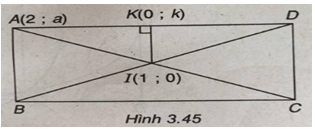
Đặt A(2 ; a); K(0 ; k); C(0 ; c); I(1 ; 0) là tọa độ các điểm đã cho ta có:
\({{a + c} \over 2} = 0 \Rightarrow c = - a.\)
\(AD = 2AB \Rightarrow AK = 2KI.\) Ta có: \(\overrightarrow {AK} = ( - 2;k - 1),\,\overrightarrow {IK} = ( - 1;k)\)
\(\left\{ \matrix{
\overrightarrow {AK} .\overrightarrow {IK} = o \hfill \cr
\left| {\overrightarrow {AK} } \right| = 2\left| {\overrightarrow {IK} } \right| \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2 + k(k - a) = 0 \hfill \cr
{\overrightarrow {AK} ^2} = 4{\overrightarrow {IK} ^2} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
k - a = - {k \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \cr
4 + {(k - a)^2} = 4(1 + {k^2})\,\,\,\,(2) \hfill \cr} \right.\)
Thay (1) vào (2) ta được:
\(\eqalign{
& 4 + {4 \over {{k^2}}} = 4\left( {1 + {k^2}} \right) \cr
& \Leftrightarrow 4{k^2} + 4 = 4{k^2} + 4{k^4} \cr
& \Leftrightarrow {k^2} = 1 \Leftrightarrow k = - 1\,\,(k < 0). \cr} \)
Suy ra a = -3.
Vậy A(2 ; -3), C(0 ; 3) và K(0 ; -1).
Ta có:
\(\eqalign{
& \overrightarrow {AD} = 2\overrightarrow {AK} \Rightarrow \left\{ \matrix{
{x_D} - 2 = 2.(0 - 2) \hfill \cr
{y_D} + 3 = 2.( - 1 + 3) \hfill \cr} \right. \cr
& \Rightarrow \left\{ \matrix{
{x_D} = 2 \hfill \cr
{y_D} = 1. \hfill \cr} \right. \cr} \)
Vậy D(-2 ; 1)
Ta có:
\(\eqalign{
& \overrightarrow {DB} = 2\overrightarrow {DI} \Rightarrow \left\{ \matrix{
{x_B} + 2 = 2.(1 + 2) \hfill \cr
{y_B} - 1 = 2.(0 - 1) \hfill \cr} \right. \cr
& \Rightarrow \left\{ \matrix{
{x_B} = 4 \hfill \cr
{y_B} = - 1. \hfill \cr} \right. \cr} \)
Vậy B(4 ; -1).
Sachbaitap.net











