Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh v..

Bài 9 trang 136 Vở bài tập toán 9 tập 2

Giải bài 9 trang 136 VBT toán 9 tập 2. Cắt mặt xung quanh của hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết bán kính hình quạt tròn bằng độ dài đường sinh...

Đề bài

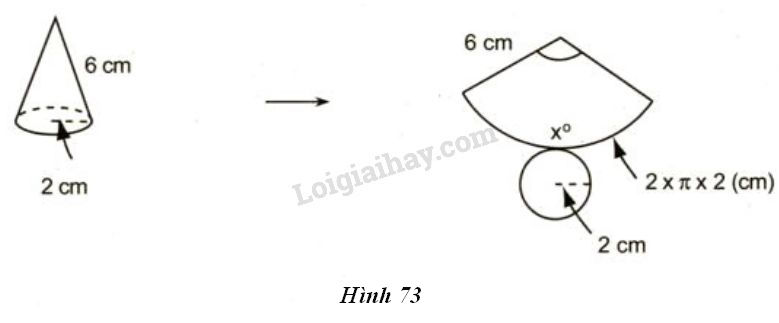
Cắt mặt xung quanh của hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết bán kính hình quạt tròn bằng độ dài đường sinh và độ dài cung bằng chu vi đáy. Quan sát hình 73 và tính số đo cung của hình quạt tròn.

Phương pháp giải - Xem chi tiết

+ Sử dụng công thức tính chu vi đường tròn bán kính \(r\) là \(C = 2\pi r.\)

+ Sử dụng công thức tính độ dài cung tròn bán kính \(R\) và số đo cung \(n^\circ \) là \(l = \dfrac{{\pi Rn}}{{180}}\)

Lời giải chi tiết

Đối với hình nón : đường sinh \(l = 6cm\), \(r = 2cm\) , \(C =2\pi r=2\pi .2= 4\pi \left( {cm} \right).\)

Đối với hình quạt : \(R = 6cm\), độ dài cung là \(l = C = 4\pi \left( {cm} \right)\).

Gọi \(x^\circ \) là số đo cung của hình quạt.

Từ công thức tính độ dài cung \(l = \dfrac{{\pi Rx}}{{180}} \Rightarrow x = \dfrac{{180.l}}{{\pi R}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)

Theo đề bài \(l = 2\pi .2 = 4\pi \) và \(R = 6cm\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)

Thay giá trị của \(l\) và \(R\) từ (2) vào (1), ta được \(x^\circ = 120^\circ \)

Vậy số đo cung của hình quạt tròn là \(120^\circ .\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 4 phiếu

Bài tiếp theo

Bài 10 trang 137 Vở bài tập toán 9 tập 2
Giải bài 10 trang 137 VBT toán 9 tập 2. Hãy điền đủ vào các ô trống (…) ở bảng sau...
Bài 11 trang 138 Vở bài tập toán 9 tập 2
Giải bài 11 trang 138 VBT toán 9 tập 2. Cái mũ của chú hề với các đường kính cho theo hình 74. Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa)...
Bài 12 trang 138 Vở bài tập toán 9 tập 2
Giải bài 12 trang 138 VBT toán 9 tập 2. Hình 75 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (OA = OB). Hãy so sánh tổng thể tích của hai hình nón và thể tích hình trụ...
Bài 13 trang 139 Vở bài tập toán 9 tập 2
Giải bài 13 trang 139 VBT toán 9 tập 2. Hãy điền đủ vào các ô trống (…) ở bảng sau...
Bài 14 trang 139 Vở bài tập toán 9 tập 2
Giải bài 14 trang 139 VBT toán 9 tập 2. Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho ở hình 76. Hãy tính: a) Thể tích của dụng cụ này...
Bài 15 trang 140 Vở bài tập toán 9 tập 2
Giải bài 15 trang 140 VBT toán 9 tập 2. Một cái xô bằng inốc có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 77 (đơn vị: cm). a) Hãy tính diện tích xung quanh của xô...
Bài 8 trang 136 Vở bài tập toán 9 tập 2
Giải bài 8 trang 136 VBT toán 9 tập 2. Một hình nón được đặt vào bên trong một hình lập phương như hình 72 (cạnh của hình lập phương bằng 1). Hãy tính a) Bán kính đáy của hình nón...
Phần câu hỏi bài 2 trang 135, 136 Vở bài tập toán 9 tập 2
Giải phần câu hỏi bài 2 trang 135, 136 VBT toán 9 tập 2. Khi quay hình tam giác vuông ABC một vòng quanh cạnh góc vuông AB cố định, ta được một hình nón. Biết rằng AB = 4cm; AC = 3cm...