Bài 1.8 trang 16 SBT hình học 11

Giải bài 1.8 trang 16 sách bài tập hình học 11. Tìm các trục đối xứng của hình vuông.

Đề bài

Tìm các trục đối xứng của hình vuông.

Phương pháp giải - Xem chi tiết

Sử dụng tính chất: Nếu một đa giác có trục đối xứng \(d\) thì qua phép đối xứng trục \(d\) mỗi đỉnh của nó phải biến thành một đỉnh của đa giác, mỗi cạnh của nó phải biến thành một cạnh của đa giác bằng cạnh ấy.

Lời giải chi tiết

Cho hình vuông \(ABCD\). Gọi \(F\) là phép đối xứng trục \(d\) biến hình vuông đó thành chính nó. Lí luận tương tự, ta thấy \(A\) chỉ có thể biến thành các điểm \(A\), \(B\), \(C\) hoặc \(D\).

- Nếu \(A\) biến thành chính nó thì \(C\) chỉ có thể biến thành chính nó và \(B\) biến thành \(D\). Từ đó suy ra \(F\) là phép đối xứng qua trục \(AC\).

- Nếu \(B\) biến thành chính nó thì \( D\) chỉ có thể biến thành chính nó và \(A\) biến thành \(C\). Từ đó suy ra \(F\) là phép đối xứng qua trục \(BD\).

- Nếu \(A\) biến thành \(B\) thì \(d\) là đường trung trực của \(AB\). Khi đó \(C\) biến thành \(D\).

- Nếu \( B\) biến thành \(C\) thì \(d\) là đường trung trực của \(BC\). Khi đó \(A\) biến thành \(D\).

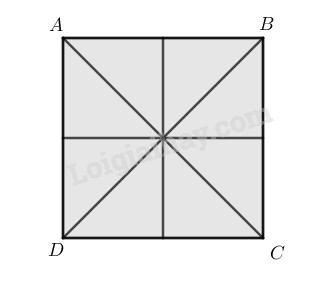
Do đó hình vuông \(ABCD\) có bốn trục đối xứng là các đường thẳng \(AC\), \(BD\) và các đường trung trực của \(AB\) và \(BC\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 5 phiếu

Bài tiếp theo

Bài 1.9 trang 16 SBT hình học 11
Giải bài 1.9 trang 16 sách bài tập hình học 11. Cho đường thẳng c, d cắt nhau và hai điểm A, B không thuộc hai đường thẳng đó. Hãy dựng điểm C trên c, điểm D trên d sao cho tứ giác ABCD là hình thang cân nhận AB là một cạnh đáy (không cần biện luận).
Bài 1.10 trang 16 SBT hình học 11
Giải bài 1.10 trang 16 sách bài tập hình học 11. Cho đường thẳng d và hai điểm A, B không thuộc d nhưng nằm cùng phía đối với d. Tìm trên d điểm M sao cho tổng các khoảng cách từ đó đến A và B là bé nhất.
Bài 1.7 trang 16 SBT hình học 11
Giải bài 1.7 trang 16 sách bài tập hình học 11. Trong mặt phẳng Oxy cho đường thẳng d có phương trình x-5y+7=0 và đường thẳng d' có phương trình 5x-y-13=0. Tìm phép đối xứng trục biến d thành d’.
Bài 1.6 trang 16 SBT hình học 11
Giải bài 1.6 trang 16 sách bài tập hình học 11. Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x+2y-6=0 và đường tròn (C) có phương trình...