Bài 3. Góc nội tiếp

Bài 16 trang 97 Vở bài tập toán 9 tập 2

Giải bài 16 trang 97 VBT toán 9 tập 2. Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC. Gọi giao điểm của MN và AC là S. Chứng minh SM=SC và SN=SA...

Đề bài

Cho \(AB, BC, CA\) là ba dây của đường tròn \((O)\). Từ điểm chính giữa \(M\) của cung \(AB\) vẽ dây \(MN\) song song với dây \(BC\). Gọi giao điểm của \(MN\) và \(AC\) là \(S\). Chứng minh \(SM=SC\) và \(SN=SA\).

Phương pháp giải - Xem chi tiết

Ta sử dụng các kiến thức sau:

+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

Từ đó chỉ ra các góc bằng nhau để có tam giác \(SMC,SAN\) cân, suy ra các cặp cạnh bằng nhau.

Lời giải chi tiết

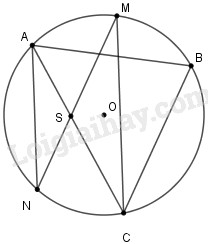
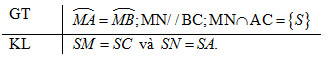
Từ giả thiết ta có \(\overparen{MB}=\overparen{MA}\)

Mà \(\overparen{NC}=\overparen{MB}\) vì \(MN//BC \Rightarrow \) \(\widehat {NMC} = \widehat {MCB}\)

\( \Rightarrow \)\(\overparen{NC}=\overparen{MA}\)

Do đó ta có \(\widehat {SMC} = \widehat {SCM}\) hay \(\Delta {\rm M}SN\) cân tại \(S \Rightarrow SM = SC.\)

Từ \(\overparen{NC}=\overparen{MA}\) ta có \(\widehat {NAC} = \widehat {ANS}\) (các góc nội tiếp chắn hai cung bằng nhau thì bằng nhau)

Hay \(\Delta ASN\) là tam giác cân tại \(S \Rightarrow SN = SA.\) (tính chất).

Loigiaihay.com

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Các bài liên quan: - Bài 3. Góc nội tiếp

Luyện Bài tập trắc nghiệm môn Toán lớp 9 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 9, luyện vào lớp 10, mọi lúc, mọi nơi môn Toán, Văn, Anh, Lý, Hóa, Sinh, Sử, Địa cùng các Thầy, Cô giáo giỏi nổi tiếng, dạy hay, dễ hiểu, dày dặn kinh nghiệm tại Tuyensinh247.com