-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI -CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Bài 2. Tỉ số lượng giác của góc nhọn
- Bài 3. Bảng lượng giác
- Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 5. Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời
- Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a khác 0) - PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số y = ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số y=ax^2 (a ≠ 0)
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Ôn tập chương 4 - Hàm số y=ax^2 (a khác 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp - Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, quạt tròn
- Ôn tập chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 13 trang 95 Vở bài tập toán 9 tập 2
Giải bài 13 trang 95 VBT toán 9 tập 2. Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O’) tại N (A nằm giữa M và N)...
Đề bài
Cho hai đường tròn bằng nhau \((O)\) và \((O’)\) cắt nhau tại \(A \) và \(B\). Vẽ đường thẳng qua \(A\) cắt \((O)\) tại \(M\) và cắt \((O’)\) tại \(N\) (\(A\) nằm giữa \(M\) và \(N\)). Hỏi \(BMN\) là tam giác gì ? Tại sao ?
Phương pháp giải - Xem chi tiết
Sử dụng các góc nội tiếp chắn các cung bằng nhau thì bằng nhau để chỉ ra các góc bằng nhau
Lời giải chi tiết
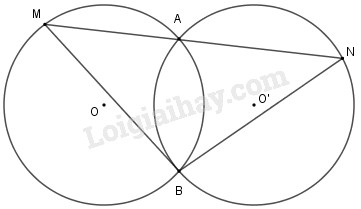
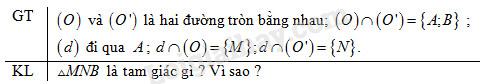
Từ giả thiết ta có cung \(AB\) của \(\left( O \right)\) và \(\left( {O'} \right)\) bằng nhau \( \Rightarrow \widehat {BMN} = \widehat {ANB}\) vì hai góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
Vậy \(\Delta MBN\) là tam giác cân tại \(B.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 14 trang 96 Vở bài tập toán 9 tập 2
- Bài 15 trang 96 Vở bài tập toán 9 tập 2
- Bài 16 trang 97 Vở bài tập toán 9 tập 2
- Bài 12 trang 95 Vở bài tập toán 9 tập 2
- Bài 11 trang 95 Vở bài tập toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
