-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 1.3 trang 8 SBT giải tích 12
Giải bài 1.3 trang 8 sách bài tập giải tích 12. Xét tính đơn điệu của các hàm số...
Xét tính đơn điệu của các hàm số:
LG câu a
a) \(y = {{\sqrt x } \over {x + 100}}\)
Phương pháp giải:
- Tìm tập xác định.
- Tính \(y'\) và tìm nghiệm của \(y'=0\).
- Xét dấu của \(y'\) và kết luận khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
Ta có: \(y' = \dfrac{{\left( {\sqrt x } \right)'\left( {x + 100} \right) - \sqrt x .\left( {x + 100} \right)'}}{{{{\left( {x + 100} \right)}^2}}}\) \( = \dfrac{{\dfrac{{x + 100}}{{2\sqrt x }} - \sqrt x }}{{{{\left( {x + 100} \right)}^2}}} = \dfrac{{100 - x}}{{2\sqrt x {{\left( {x + 100} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow x = 100\).
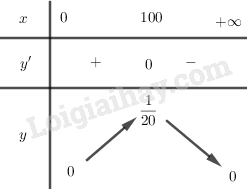
Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng \((0; 100)\) và nghịch biến trên khoảng \((100; +∞)\)
LG câu b
b) \(y = {{{x^3}} \over {\sqrt {{x^2} - 6} }}\)
Phương pháp giải:
- Tìm tập xác định.
- Tính \(y'\) và tìm nghiệm của \(y'=0\).
- Xét dấu của \(y'\) và kết luận khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
TXĐ: \((-∞; -\sqrt 6 ) ∪ (\sqrt 6; +∞)\)
\(y' = {{2{x^2}({x^2} - 9)} \over {({x^2} - 6)\sqrt {{x^2} - 6} }}\) ;\(y' = 0 \Leftrightarrow x = \pm 3\)
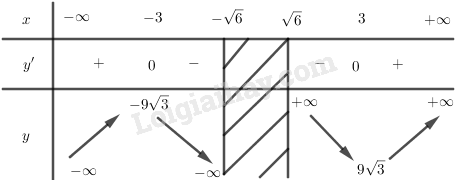
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng \((-∞; -3), (3; +∞)\), nghịch biến trên các khoảng \((-3;-\sqrt 6 ), (\sqrt 6 ; 3)\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.4 trang 8 SBT Giải tích 12
- Bài 1.5 trang 8 SBT giải tích 12
- Bài 1.6 trang 8 SBT giải tích 12
- Bài 1.7 trang 8 SBT giải tích 12
- Bài 1.8 trang 8 SBT giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
