Bài 1.3 trang 10 SBT hình học 11

Giải bài 1.3 trang 10 sách bài tập hình học 11. Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x-y-9=0. Tìm phép tịnh tiến theo vectơ có phương song song với trục Ox biến d thành đường thẳng d' đi qua gốc tọa độ và viết phương trình đường thẳng d'.

Đề bài

Trong mặt phẳng \(Oxy\) cho đường thẳng \(d\) có phương trình \(3x-y-9=0\). Tìm phép tịnh tiến theo vectơ có phương song song với trục \(Ox\) biến \(d\) thành đường thẳng \(d’\) đi qua gốc tọa độ và viết phương trình đường thẳng \(d’\).

Phương pháp giải - Xem chi tiết

Tìm điểm đầu, điểm cuối của vectơ tịnh tiến lần lượt thuộc đường thẳng \(d\) và \(d’\).

Tính chất của phép tịnh tiến: Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với đường thẳng ban đầu để tìm phương trình đường thẳng \(d’\).

Lời giải chi tiết

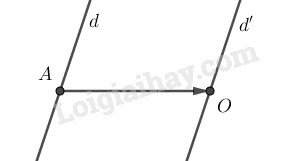
Giao của \(d\) với trục \(Ox\) là điểm \(A(3;0)\), giao của \(d'\) với trục \(Ox\) là gốc tọa độ.

Phép tịnh tiến theo vectơ \(\vec v\) biến d thành d', vectơ \(\vec v\) có giá song song với Ox.

=> Phép tịnh tiến theo vectơ \(\vec v\) biến A thành O

Do đó \(\vec v= \vec {OA}= (3;0)\)

Đường thẳng \(d’\) song song với \(d\) và đi qua gốc tọa độ nên nó có phương trình \(3x-y=0\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4 trên 10 phiếu

Bài tiếp theo

Bài 1.4 trang 10 SBT hình học 11
Giải bài 1.4 trang 10 sách bài tập hình học 11. Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x...
Bài 1.5 trang 10 SBT hình học 11
Giải bài 1.5 trang 10 sách bài tập hình học 11. Cho đoạn thẳng AB và đường tròn (C) tâm O, bán kính r nằm về một phía của đường thẳng AB. Lấy điểm M trên (C), rồi dựng hình bình hành ABMM'. Tìm tập hợp các điểm M' khi M di động trên (C).
Bài 1.2 trang 10 SBT hình học 11
Giải bài 1.2 trang 10 sách bài tập hình học 11. Trong mặt phẳng Oxy cho...
Bài 1.1 trang 10 SBT hình học 11
Giải bài 1.1 trang 10 sách bài tập hình học 11. Trong mặt phẳng tọa độ Oxy cho...