Giải SBT toán hình học và đại số 11 nâng cao Bài 2. Dãy số

Câu 3.14 trang 87 sách bài tập Đại số và Giải tích 11 Nâng cao


Trong mặt phẳng tọa độ, đồ thị (C) của hàm số

Đề bài

Trong mặt phẳng tọa độ, đồ thị (C) của hàm số \(y = 2x + 1.\) Trên (C) lấy điểm \({A_1}\) có hoành độ bằng \({1 \over 3}.\) Qua \({A_1}\) kẻ một đường thẳng song song với trục hoành cắt đường thẳng \(\Delta \) chứa đường phân giác của góc phần tư thứ nhất tại điểm \({B_1};\) gọi \({A_2}\) là giao điểm của (C) với đường thẳng đi qua \({B_1}\)  và song song với trục tung. Với điểm \({A_2},\) lại thực hiện các bước tương tự như đã làm với điểm \({A_1}\) ta sẽ được điểm \({A_3}.\) Với điểm \({A_3},\) lại làm như thế với điểm \({A_4}.\) Cứ tiếp tục mãi quá trình trên, ta sẽ được một dãy vô hạn các điểm \({A_1},{A_2},{A_3},{A_4},...\) nằm trên đồ thị (C), (h.3.1)

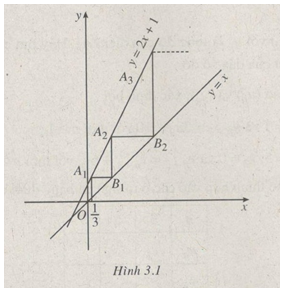
Với mỗi số nguyên dương n, gọi \({u_n}\) là hoành độ của điểm \({A_n}.\) Hãy cho dãy số \(\left( {{u_n}} \right)\) bởi hệ thức truy hồi.

 

Lời giải chi tiết

- Phương trình của đường thẳng \(\Delta :y = x\)

- Với mỗi \(n \ge 1,\) kí hiệu \({a_n}\) và \({b_n}\) tương ứng là tung độ của điểm \({A_n}\) và điểm \({B_{n.}}\) Khi đó:

- Do \({A_n}\) nằm trên (C) nên \({a_n} = 2{u_n} + 1\)

- Do \({B_n}\) nằm trên đường thẳng đi qua \({A_n}\) và song song với trục hoành nên \({b_n} = {a_n} = 2{u_n} + 1\)

- Do \({B_n}\) nằm trên đường thẳng đi qua \({A_{n + 1}}\) và song song với trục tung nên hoành độ của nó bằng \({u_{n + 1}}\)

Từ đó, do \({B_n}\) nằm trên \(\Delta \) nên \({u_{n + 1}} = {b_n} = 2{u_n} + 1\) với mọi \(n \ge 1\)

Vậy, dãy số \(\left( {{u_n}} \right)\) được xác định bởi \({u_1} = {1 \over 3}\) và \({u_{n + 1}} = 2{u_n} + 1\) với mọi \(n \ge 1\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store