-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Giải SBT toán hình học và giải tích 12 nâng cao
Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số h..
Bài 1.58 trang 22 SBT Giải tích 12 Nâng cao
Giải bài 1.58 trang 22 sách bài tập Giải tích 12 Nâng cao. Tìm các giá trị m sao cho hàm số...
LG a
Tìm các giá trị m sao cho hàm số
\(y = {{ - 2{x^2} + (m + 2)x - 3m + 1} \over {x - 1}}\)
Nghịch biến trên mỗi khoảng xác định của nó.
Lời giải chi tiết:
Ta viết hàm số đã cho dưới dạng
\(y = - 2x + m + {{1 - 2m} \over {x - 1}}\)
Khi đó: \(y' = - 2 + {{2m - 1} \over {{{(x - 1)}^2}}}\)
+) Nếu \(2m - 1 \le 0\) hay \(m \le {1 \over 2}\) thì \(y' < 0\) với mọi \(x \ne 1\).
Do đó hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)
+) Dễ thấy nếu \(2m - 1 > 0\) hay \(m > {1 \over 2}\) thì phương trình \(y' = 0\) có hai nghiệm \({x_1},{x_2}\) trong đó \({x_1} < 1 < {x_2}\)
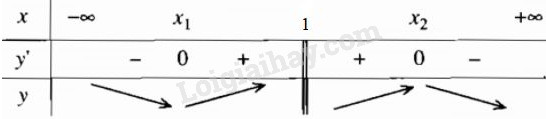
Hàm số đồng biến trên mỗi khoảng \(\left( {{x_1};1} \right)\) và \(\left( {1;{x_2}} \right)\).
Trong trường hợp này, các giá trị của m không thỏa mãn điều kiện đòi hỏi.
LG b
Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 0.
Lời giải chi tiết:
Với \(m = 0\) ta được \(y = \frac{{ - 2{x^2} + 2x + 1}}{{x - 1}} = - 2x + \frac{1}{{x - 1}}\)
+) TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
+) Chiều biến thiên:
\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty \) nên TCĐ: \(x = 1\).
\(\mathop {\lim }\limits_{x \to \pm \infty } \left( {y + 2x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( {\frac{1}{{x - 1}}} \right) = 0\) nên TCX: \(y = x - 1\).
Ta có:
\(y' = - 2 - \frac{1}{{{{\left( {x - 1} \right)}^2}}} < 0,\forall x \in D\)
Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) và không có cực trị.
BBT:
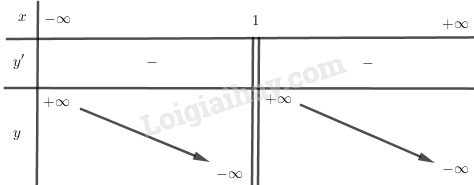
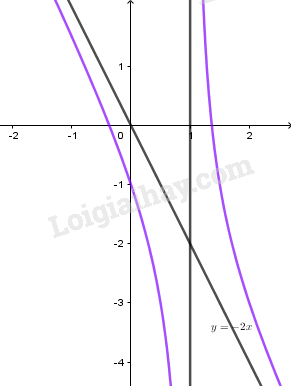
+) Đồ thị:
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.57 trang 21 SBT Giải tích 12 Nâng cao
- Bài 1.56 trang 21 SBT Giải tích 12 Nâng cao
- Bài 1.55 trang 21 SBT Giải tích 12 Nâng cao
- Bài 1.54 trang 21 SBT Giải tích 12 Nâng cao
- Bài 1.53 trang 21 SBT Giải tích 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
