-
Khảo sát chất lượng đầu năm
-
Chương 1 Căn bậc hai - Căn bậc ba
-
Chương 2 Hàm số bậc nhất
-
Chương 3 Hệ hai phương trình bậc nhất hai ẩn
- Bài 1: Phương trình bậc nhất hai ẩn
- Bài 2: Hệ hai phương trình bậc nhất hai ẩn
- Bài 3: Giải hệ phương trình bằng phương pháp thế
- Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
- Hệ phương trình bậc nhất hai ẩn chứa tham số
- Bài 5,6: Giải bài toán bằng cách lập hệ phương trình
- Bài tập hay và khó chương 3 về hệ phương trình
- Bài tập ôn tập chương 3
-
Chương 4 Hàm số y=ax^2. Phương trình bậc hai một ẩn
- Bài 1,2: Hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2
- Bài 3,4: Phương trình bậc hai một ẩn và công thức nghiệm
- Bài 5: Công thức nghiệm thu gọn
- Bài 6: Hệ thức Vi-ét và ứng dụng
- Bài 7: Phương trình quy về phương trình bậc hai
- Sự tương giao giữa đường thẳng và Parabol
- Bài 8: Giải bài toán bằng cách lập phương trình
- Hệ phương trình đối xứng
- Bài tập hay và khó chương 4: Sự tương giao của đường thẳng và parabol
- Tổng hợp câu hay và khó về giải bài toán bằng cách lập phương trình, hệ phương trình
- Tổng hợp câu hay và khó về hệ thức Vi-et
- Bài tập ôn tập chương 4
-
Chương 5 Hệ thức lượng trong tam giác vuông
-
Chương 6 Đường tròn
- Sự xác định của đường tròn- Tính chất đối xứng của đường tròn
- Bài 2: Đường kính và dây của đường tròn
- Bài 4: Vị trí tương đối giữa đường thẳng và đường tròn
- Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6: Tính chất hai tiếp tuyến cắt nhau
- Bài 7,8: Vị trí tương đối của hai đường tròn
- Bài tập hay và khó chương đường tròn
- Bài tập ôn tập chương 6
-
Chương 7 Góc với đường tròn
- Bài 1: Góc ở tâm- Số đo cung
- Bài 2: Liên hệ giữa cung và dây
- Bài 3: Góc nội tiếp
- Bài 4: Góc tạo bởi tiếp tuyến và dây cung
- Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn
- Bài 6: Cung chứa góc
- Bài 7: Tứ giác nội tiếp
- Bài 8: Đường tròn ngoại tiếp, đường tròn nội tiếp
- Bài 9: Độ dài đường tròn, cung tròn
- Bài 10: Diện tích hình tròn, quạt tròn
- Bài tập hay và khó chương góc với đường tròn
- Bài tập vận dụng cao từ các đề thi chuyên
- Bài tập ôn tập chương 7
-
Chương 8 Hình trụ - hình nón - hình cầu
Trắc nghiệm Đề thi khảo sát chất lượng đầu năm - Đề số 1
Đề bài
Cho hình vẽ, biết \(DE// BC\). Khẳng định nào sau đây là đúng?
-
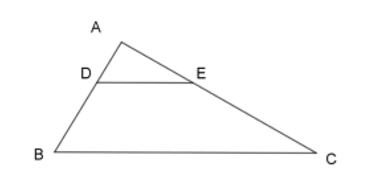
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\)
-
B.
\(AD.AE = AB.AC\)
-
C.
\(\dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC}}\)
-
D.
\(DE.AD = AB.BC\)
Khi \(x \ge 3\), kết quả rút gọn của biểu thức \(2{\rm{x}} + \left| {x - 3} \right| - 1\) là:
-
A.
\(3x + 2\)
-
B.
\(3x - 4\)
-
C.
\(x + 2\)
-
D.
\(4 - 3x\)
Diện tích toàn phần của hình lập phương có độ dài cạnh đáy bằng 5cm là:
-
A.
\(25\,c{m^2}\)
-
B.
\(125\,c{m^2}\)
-
C.
\(150\,c{m^2}\)
-
D.
\(250\,c{m^2}\)
Cho \(\Delta MNP \backsim \Delta HGK\) có tỉ số chu vi: \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}.\) Chọn câu đúng.
-
A.
\(\dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)
-
B.
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{2}{7}\)
-
C.
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{{49}}{4}\)
-
D.
\(\dfrac{{NP}}{{GK}} = \dfrac{5}{7}\)
Giá trị \(x = 2\) là nghiệm của bất phương trình nào dưới đây?
-
A.
\(2x + 5 > 11\)
-
B.
\(4-x > 3x-1\)
-
C.
\( - 4{\rm{x}} + 7 > x - 1\)
-
D.
\({x^2} + 3 > 6x-7\)
Rút gọn biểu thức \({\left( {x + y} \right)^2} + {\rm{ }}{\left( {x - y} \right)^2}\), ta được kết quả là:
-
A.
\(2\left( {{x^2} + {\rm{ }}{y^2}} \right)\)
-
B.
\(2{x^2} + {\rm{ }}{y^2}\)
-
C.
\(2\left( {{x^2} - {\rm{ }}{y^2}} \right)\)
-
D.
Một kết quả khác
Phân tích đa thức \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\) thành nhân tử ta được:
-
A.
\(5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
-
B.
\(5{x^2}{y^3}\left( { - 5xy + 2x} \right)\)
-
C.
\({x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
-
D.
\(5{x^2}{y^3}\left( {1 - xy + x} \right)\)
Phương trình \(7x + 4\; = 3x-{\rm{ }}1\) có tập nghiệm là:
-
A.
\(S = \left\{ {\dfrac{{ - 5}}{4}} \right\}\)
-
B.
\(S = \left\{ {\dfrac{5}{4}} \right\}\)
-
C.
\(S = \left\{ { - 1} \right\}\)
-
D.
\(S = \left\{ 0 \right\}\)
Phương trình \({x^3} - 9x = 0\) có bao nhiêu nghiệm?
-
A.
\(1\)
-
B.
\(3\)
-
C.
\(4\)
-
D.
\(2\)
Phương trình \(\left| {x - 4} \right| + 3x = 5\) có tổng các nghiệm là:
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{{11}}{4}\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(1\)
Giải phương trình \(\dfrac{{x + 5}}{{x - 5}} - \dfrac{{x - 5}}{{x + 5}} = \dfrac{{20}}{{{x^2} - 25}}\) ta được nghiệm là:
-
A.
\(x = 5\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = -1\)
Cho biểu thức: \(Q = \left( {\dfrac{{{x^2} - 1}}{{x - 1}} + \dfrac{{{x^3} - 1}}{{1 - {x^2}}}} \right):\dfrac{{2{x^2} - 4x + 2}}{{{x^2} - 1}}\quad \left( {x \ne \pm {\rm{ }}1} \right)\).
Rút gọn Q ta được:
-
A.
\(Q = \dfrac{x}{{x - 1}}\)
-
B.
\(Q = \dfrac{{2x}}{{x - 1}}\)
-
C.
\(Q = \dfrac{x}{{2\left( {x + 1} \right)}}\)
-
D.
\(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\)
Tìm \(x\) biết \(Q = 3.\)
-
A.
\(x = 6\)
-
B.
\(x = 3\)
-
C.
\(x = \dfrac{6}{5}\)
-
D.
\(x = \dfrac{5}{6}\)
Tìm \(x\) sao cho \(\left| {\rm{Q}} \right| > {\rm{Q}}\).
-
A.
\({\rm{ 0 < x < 1}}\)
-
B.
\(x > 1\)
-
C.
\(x > 0\)
-
D.
\(x < 1\)
Một người đi xe máy từ A đến B với vận tốc trung bình 30km/giờ. Khi đi được 1 giờ thì xe bị hỏng, người đó phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xong người đó đi tiếp tới B, để đến B đúng giờ đã định người đó phải tăng vận tốc thêm 6km/h. Tính độ dài quãng đường AB.
-
A.
\(60\,km\)
-
B.
\(120\,km\)
-
C.
\(90\,km\)
-
D.
\(150\,km\)
Cho \(\Delta ABC\) kẻ các đường cao \(BD\) và \(CE\) (\(D \in AC{\rm{ ; E}} \in {\rm{AB}}\)). \(BD\) và \(CE\) cắt nhau tại \(H.\)
Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm I và K sao cho \(\widehat {{\rm{AIC}}}{\rm{ = }}\widehat {{\rm{AKB }}}{\rm{ = 9}}{{\rm{0}}^{\rm{0}}}.\) Khi đó tam giác \(AIK\) là:
-
A.
tam giác cân tại \(I\)
-
B.
tam giác cân tại \(K\)
-
C.
tam giác cân tại \(A\)
-
D.
tam giác đều
Cho \(\widehat {{\rm{AED}}} = {40^0}\). Tính số đo \(\widehat {{\rm{HBC}}}\).
-
A.
\(\widehat {{\rm{HBC}}} = {60^0}\)
-
B.
\(\widehat {{\rm{HBC}}} = {50^0}\)
-
C.
\(\widehat {{\rm{HBC}}} = {40^0}\)
-
D.
\(\widehat {{\rm{HBC}}} = {35^0}\)
Hệ thức nào dưới đây đúng?
-
A.
\(BH.BD + CH.CE = A{B^2}\)
-
B.
\(BH.BD + CH.CE = A{C^2}\)
-
C.
\(BH.BD + CH.CE = 2B{C^2}\)
-
D.
\(BH.BD + CH.CE = B{C^2}\)
Tích \(AE{\rm{ }}.{\rm{ }}AB\;\) bằng:
-
A.
\(AC.AD\)
-
B.
\(AH.AC\)
-
C.
\(A{B^2}\)
-
D.
\(AH.AD\)
Cho \(a,b,c > 0\) thỏa mãn: \(6a + 2b + 3c = 11.\) Tìm giá trị nhỏ nhất của biểu thức \(M = \dfrac{{2b + 3c + 16}}{{1 + 6a}} + \dfrac{{6a + 3c + 16}}{{1 + 2b}} + \dfrac{{6a + 2b + 16}}{{1 + 3c}}\).
-
A.
\(8\)
-
B.
\(9\)
-
C.
\(15\)
-
D.
\(11\)
Lời giải và đáp án
Cho hình vẽ, biết \(DE// BC\). Khẳng định nào sau đây là đúng?
-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\)
-
B.
\(AD.AE = AB.AC\)
-
C.
\(\dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC}}\)
-
D.
\(DE.AD = AB.BC\)
Đáp án : A
Áp dụng định lý Talet để tìm ra tỉ lệ thức phù hợp, từ đó thực hiện yêu cầu của bài toán.
Áp dụng định lý Ta lét, ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow \) Đáp án A đúng.
Vì \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) nên \(AD.AC = AB.AE\)
\( \Rightarrow \) Đáp án B sai.
Ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow \)\(\dfrac{{AD}}{{AB - AD}} = \dfrac{{DE}}{{BC}} \Leftrightarrow \dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC - DE}}\)
\( \Rightarrow \) Đáp án C sai.
Ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow AD.BC = AB.DE\)
\( \Rightarrow \) Đáp án D sai.
Khi \(x \ge 3\), kết quả rút gọn của biểu thức \(2{\rm{x}} + \left| {x - 3} \right| - 1\) là:
-
A.
\(3x + 2\)
-
B.
\(3x - 4\)
-
C.
\(x + 2\)
-
D.
\(4 - 3x\)
Đáp án : B
Áp dụng định nghĩa giá trị tuyệt đối của một số hữu tỉ để rút gọn biểu thức: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,khi\,\,x \ge 0\\ - x\,\,khi\,\,x < 0\end{array} \right.\)
Khi \(x \ge 3\) thì \(\left| {x - 3} \right| = x - 3,\) ta có biểu thức:
\(2x + \left| {x - 3} \right| - 1 = 2x + x - 3 - 1 = 3x - 4.\)
Diện tích toàn phần của hình lập phương có độ dài cạnh đáy bằng 5cm là:
-
A.
\(25\,c{m^2}\)
-
B.
\(125\,c{m^2}\)
-
C.
\(150\,c{m^2}\)
-
D.
\(250\,c{m^2}\)
Đáp án : C
Công thức tính diện tích toàn phần của hình lập phương cạnh \(a\) là: \(6{a^2}.\)
Diện tích toàn phần của hình lập phương có độ dài cạnh đáy bằng 5cm là: \({S_{tp}} = {6. 5^2} = 150\,c{m^2}.\)
Cho \(\Delta MNP \backsim \Delta HGK\) có tỉ số chu vi: \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}.\) Chọn câu đúng.
-
A.
\(\dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)
-
B.
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{2}{7}\)
-
C.
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{{49}}{4}\)
-
D.
\(\dfrac{{NP}}{{GK}} = \dfrac{5}{7}\)
Đáp án : A
+) Áp dụng lý thuyết về mối quan hệ giữa tỉ số diện tích hai tam giác đồng dạng và tỉ số đồng dạng của 2 tam giác, kết hợp với dữ kiện đề bài cho để thực hiện yêu cầu của bài toán.
Lưu ý: Tỉ số đồng dạng bằng tỉ số chu vi và tỉ số diện tích bằng bình phương tỉ số đồng dạng.
Gọi k là tỉ số đồng dạng của 2 tam giác MNP và HGK.
Theo bài ta có:
\(\Delta MNP \backsim \Delta HGK\) và \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}\)
\( \Rightarrow \dfrac{{MN}}{{HG}} = \dfrac{{NP}}{{GK}} = \dfrac{{MP}}{{HK}} \)\(=\dfrac{MN+NP+MP}{HG+GK+HK}= \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7} = k\)
Do đó: \( \dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)
Và \( \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = {k^2} = {\left( {\dfrac{2}{7}} \right)^2} = \dfrac{4}{{49}}.\)
Giá trị \(x = 2\) là nghiệm của bất phương trình nào dưới đây?
-
A.
\(2x + 5 > 11\)
-
B.
\(4-x > 3x-1\)
-
C.
\( - 4{\rm{x}} + 7 > x - 1\)
-
D.
\({x^2} + 3 > 6x-7\)
Đáp án : D
Giải các bất phương trình ở các đáp án sau đó xem \(x = 2\) có thuộc tập nghiệm của bất phương trình nào thì chọn đáp án đó.
Ta có:
+) Đáp án A: \(2x + 5 > 11 \Leftrightarrow 2x > 6 \)\(\Leftrightarrow x > 3 \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.
+) Đáp án B: \(4 - x > 3x - 1 \Leftrightarrow 4 + 1 > 3x + x \Leftrightarrow 4x < 5\)\( \Leftrightarrow x < \dfrac{5}{4} \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.
+) Đáp án C: \( - 4x + 7 > x - 1 \Leftrightarrow 7 + 1 > x + 4x \Leftrightarrow 5x < 8\)\( \Leftrightarrow x < \dfrac{8}{5} \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.
+) Đáp án D: \({x^2} + 3 > 6x - 7 \Leftrightarrow {x^2} - 6x + 10 > 0\)
Thay \(x = 2\) vào vế trái của bất phương trình ta có: \({2^2} - 6.2 + 10 = 2 > 0\) (luôn đúng)
\( \Rightarrow x = 2\) là nghiệm của bất phương trình.
Rút gọn biểu thức \({\left( {x + y} \right)^2} + {\rm{ }}{\left( {x - y} \right)^2}\), ta được kết quả là:
-
A.
\(2\left( {{x^2} + {\rm{ }}{y^2}} \right)\)
-
B.
\(2{x^2} + {\rm{ }}{y^2}\)
-
C.
\(2\left( {{x^2} - {\rm{ }}{y^2}} \right)\)
-
D.
Một kết quả khác
Đáp án : A
Sử dụng các hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2};\,{\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\).
Ta có: \({\left( {x + y} \right)^2} + {\rm{ }}{\left( {x - y} \right)^2}\)\( = {x^2} + 2xy + {y^2} + {x^2} - 2xy + {y^2}\)\( = 2{x^2} + 2{y^2} = 2\left( {{x^2} + {y^2}} \right)\).
Phân tích đa thức \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\) thành nhân tử ta được:
-
A.
\(5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
-
B.
\(5{x^2}{y^3}\left( { - 5xy + 2x} \right)\)
-
C.
\({x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
-
D.
\(5{x^2}{y^3}\left( {1 - xy + x} \right)\)
Đáp án : A
Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.
Ta có: \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\)\( = 5{x^2}{y^3}. 1 - 5{x^2}{y^3}. 5xy + 5{x^2}{y^3}. 2x\)\( = 5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\).
Phương trình \(7x + 4\; = 3x-{\rm{ }}1\) có tập nghiệm là:
-
A.
\(S = \left\{ {\dfrac{{ - 5}}{4}} \right\}\)
-
B.
\(S = \left\{ {\dfrac{5}{4}} \right\}\)
-
C.
\(S = \left\{ { - 1} \right\}\)
-
D.
\(S = \left\{ 0 \right\}\)
Đáp án : A
Sử dụng quy tắc chuyển vế để biến đổi đưa phương trình về dạng phương trình bậc nhất một ẩn \(ax + b = 0 \Leftrightarrow x = - \dfrac{b}{a}\,\left( {a \ne 0} \right)\).
Ta có: \(7x + 4\; = 3x-{\rm{ }}1\)
\(\begin{array}{l} \Leftrightarrow 7x - 3x = - 1 - 4\\ \Leftrightarrow 4x = - 5\\ \Leftrightarrow x = - \dfrac{5}{4}\end{array}\).
Vậy phương trình có tập nghiệm là \(S = \left\{ {\dfrac{{ - 5}}{4}} \right\}\).
Phương trình \({x^3} - 9x = 0\) có bao nhiêu nghiệm?
-
A.
\(1\)
-
B.
\(3\)
-
C.
\(4\)
-
D.
\(2\)
Đáp án : B
Phân tích vế trái thành nhân tử đưa phương trình về dạng \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)
Ta có: \({x^3} - 9x = 0\)\( \Leftrightarrow x\left( {{x^2} - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 9 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\\x = - 3\end{array} \right.\)
Vậy phương trình có tập nghiệm \(S = \left\{ { - 3;0;3} \right\}\).
Hay phương trình đã cho có ba nghiệm phân biệt.
Phương trình \(\left| {x - 4} \right| + 3x = 5\) có tổng các nghiệm là:
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{{11}}{4}\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(1\)
Đáp án : C
Sử dụng \(\left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\,A < 0\end{array} \right.\) để đưa về phương trình bậc nhất một ẩn.
Xét phương trình \(\left| {x - 4} \right| + 3x = 5\).
TH1: \(\left| {x - 4} \right| = x - 4\) với \(x - 4 \ge 0 \Leftrightarrow x \ge 4\)
Khi đó ta có phương trình: \(x - 4 + 3x = 5 \Leftrightarrow 4x = 9 \Leftrightarrow x = \dfrac{9}{4}\) (loại vì \(x \ge 4\))
TH2: \(\left| {x - 4} \right| = - x + 4\) với \(x - 4 < 0 \Leftrightarrow x < 4\)
Khi đó ta có phương trình \( - x + 4 + 3x = 5\)\( \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}\) (nhận)
Vậy phương trình đã cho có một nghiệm là \(x = \dfrac{1}{2}.\)
Giải phương trình \(\dfrac{{x + 5}}{{x - 5}} - \dfrac{{x - 5}}{{x + 5}} = \dfrac{{20}}{{{x^2} - 25}}\) ta được nghiệm là:
-
A.
\(x = 5\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = -1\)
Đáp án : C
Sử dụng các bước giải phương trình chứa ẩn ở mẫu thức:
+ Tìm ĐKXĐ
+ Quy đồng mẫu rồi khử mẫu.
+ Giải phương trình vừa nhận được.
+ Đối chiếu điều kiện rồi kết luận nghiệm.
ĐKXĐ: \(x \ne \pm 5\)
Ta có: \(\dfrac{{x + 5}}{{x - 5}} - \dfrac{{x - 5}}{{x + 5}} = \dfrac{{20}}{{{x^2} - 25}}\).
\( \Leftrightarrow \dfrac{{{{\left( {x + 5} \right)}^2} - {{\left( {x - 5} \right)}^2}}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} = \dfrac{{20}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\)
\(\begin{array}{l} \Rightarrow {\left( {x + 5} \right)^2} - {\left( {x - 5} \right)^2} = 20\\ \Leftrightarrow {x^2} + 10x + 25 - {x^2} + 10x - 25 = 20\\ \Leftrightarrow 20x = 20\\ \Leftrightarrow x = 1\left( {tm} \right)\end{array}\)
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ 1 \right\}\).
Cho biểu thức: \(Q = \left( {\dfrac{{{x^2} - 1}}{{x - 1}} + \dfrac{{{x^3} - 1}}{{1 - {x^2}}}} \right):\dfrac{{2{x^2} - 4x + 2}}{{{x^2} - 1}}\quad \left( {x \ne \pm {\rm{ }}1} \right)\).
Rút gọn Q ta được:
-
A.
\(Q = \dfrac{x}{{x - 1}}\)
-
B.
\(Q = \dfrac{{2x}}{{x - 1}}\)
-
C.
\(Q = \dfrac{x}{{2\left( {x + 1} \right)}}\)
-
D.
\(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\)
Đáp án: D
Ta sử dụng các quy tắc cộng, trừ, nhân, chia các phân thức và các hằng đẳng thức để rút gọn biểu thức.
\(Q = \left( {\dfrac{{{x^2} - 1}}{{x - 1}} + \dfrac{{{x^3} - 1}}{{1 - {x^2}}}} \right):\dfrac{{2{x^2} - 4x + 2}}{{{x^2} - 1}}\quad \left( {x \ne \pm 1} \right)\)
\(Q = \left( {\dfrac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}} - \dfrac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}} \right):\dfrac{{2{{\left( {x - 1} \right)}^2}}}{{{x^2} - 1}}\)
\(Q = \left( {\dfrac{{x + 1}}{1} - \dfrac{{{x^2} + x + 1}}{{x + 1}}} \right):\dfrac{{2\left( {x - 1} \right)}}{{x + 1}}\)
\(Q = \dfrac{{{{\left( {x + 1} \right)}^2} - {x^2} - x - 1}}{{x + 1}}.\dfrac{{x + 1}}{{2\left( {x - 1} \right)}}\)
\(\begin{array}{l}Q = \dfrac{{{x^2} + 2x + 1 - {x^2} - x - 1}}{{x + 1}}.\dfrac{{x + 1}}{{2\left( {x - 1} \right)}}\\Q = \dfrac{x}{{2\left( {x - 1} \right)}}\end{array}\)
Vậy \(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\) với mọi \(x \ne \pm 1\).
Tìm \(x\) biết \(Q = 3.\)
-
A.
\(x = 6\)
-
B.
\(x = 3\)
-
C.
\(x = \dfrac{6}{5}\)
-
D.
\(x = \dfrac{5}{6}\)
Đáp án: C
Ta sử dụng kết quả câu trước \(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\) với mọi \(x \ne \pm 1\)
Thay \(Q = 3\) rồi giải phương trình chứa ẩn ở mẫu thu được để tìm \(x.\)
Theo kết quả câu trước \(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\) với mọi \(x \ne \pm 1\).
Để \(Q = 3\) thì \(\dfrac{x}{{2\left( {x - 1} \right)}} = 3 \Rightarrow x = 3. 2\left( {x - 1} \right)\)
\( \Leftrightarrow x = 6x - 6 \Leftrightarrow 6x - x = 6 \Leftrightarrow 5x = 6\)\( \Leftrightarrow x = \dfrac{6}{5}\;\left( {tm} \right)\)
Vậy \(x = \dfrac{6}{5}\) thì \(Q = 3.\)
Tìm \(x\) sao cho \(\left| {\rm{Q}} \right| > {\rm{Q}}\).
-
A.
\({\rm{ 0 < x < 1}}\)
-
B.
\(x > 1\)
-
C.
\(x > 0\)
-
D.
\(x < 1\)
Đáp án: A
Ta sử dụng kết quả câu trước \(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\) với mọi \(x \ne \pm 1\).
Từ đó dựa vào định nghĩa dấu giá trị tuyệt đối: Sử dụng \(\left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\,A < 0\end{array} \right.\)
Ta có \(\left| {\rm{Q}} \right|{\rm{ }} > {\rm{ Q }} \Leftrightarrow {\rm{ Q < 0}}\)
Khi đó ta được: \(\dfrac{x}{{2\left( {x - 1} \right)}}\) < 0 \(\forall x \ne \pm 1\)
TH1: \(\left\{ \begin{array}{l}x < 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 0\\x > 1\end{array} \right.\) không xảy ra.
TH2: \(\left\{ \begin{array}{l}x > 0\\x - 1 < 0\end{array} \right. \Leftrightarrow {\rm{ 0 < x < 1}}\).
Vậy với \({\rm{ 0 < x < 1}}\) thì \(\left| {\rm{Q}} \right|{\rm{ }} > {\rm{ Q}}\).
Một người đi xe máy từ A đến B với vận tốc trung bình 30km/giờ. Khi đi được 1 giờ thì xe bị hỏng, người đó phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xong người đó đi tiếp tới B, để đến B đúng giờ đã định người đó phải tăng vận tốc thêm 6km/h. Tính độ dài quãng đường AB.
-
A.
\(60\,km\)
-
B.
\(120\,km\)
-
C.
\(90\,km\)
-
D.
\(150\,km\)
Đáp án : A
Giải theo các bước sau:
+ Lập phương trình: Chọn ẩn và đặt điều kiện; biểu diễn đại lượng chưa biết theo ẩn và đại lượng đã biết; lập phương trình biểu thị mối quan hệ giữa các đại lượng
+ Giải phương trình
+ Đối chiếu điều kiện rồi kết luận
Đổi 10 phút = \(\dfrac{1}{6}\) giờ.
Gọi quãng đường AB dài là \(x\left( {km} \right)\left( {x > 30{\rm{ }}} \right)\).
Suy ra quãng đường từ khi dừng lại sửa xe đến B là \(x- 30{\rm{ }}\left( {km} \right)\).
Thời gian dự định đi từ A đến B là \(\dfrac{x}{{30}}\)(h).
Thời gian thực tế đi từ A đến B là \(1 + \dfrac{1}{6} + \dfrac{{x - 30}}{{36}}\) (h).
Ta có phương trình:
\(1 + \dfrac{1}{6} + \dfrac{{x - 30}}{{36}} = \dfrac{x}{{30}}\)
\( \Leftrightarrow \dfrac{{36 + 6 + x - 30}}{{36}} = \dfrac{x}{{30}}\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{12 + x}}{{36}} = \dfrac{x}{{30}}\\ \Rightarrow 30\left( {12 + x} \right) = 36.x\\ \Leftrightarrow 360 + 30x = 36x\\ \Leftrightarrow 6x = 360\\ \Leftrightarrow x = 60\left( {tm} \right)\end{array}\)
Vậy quãng đường \(AB\) dài \(60\) km.
Cho \(\Delta ABC\) kẻ các đường cao \(BD\) và \(CE\) (\(D \in AC{\rm{ ; E}} \in {\rm{AB}}\)). \(BD\) và \(CE\) cắt nhau tại \(H.\)
Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm I và K sao cho \(\widehat {{\rm{AIC}}}{\rm{ = }}\widehat {{\rm{AKB }}}{\rm{ = 9}}{{\rm{0}}^{\rm{0}}}.\) Khi đó tam giác \(AIK\) là:
-
A.
tam giác cân tại \(I\)
-
B.
tam giác cân tại \(K\)
-
C.
tam giác cân tại \(A\)
-
D.
tam giác đều
Đáp án: C
Chứng minh các cặp tam giác đồng dạng \(\Delta AID \backsim \Delta ACI\) và \(\Delta AEK \backsim \Delta AKB\).
Từ đó suy ra các cặp cạnh tương ứng để lập luận.
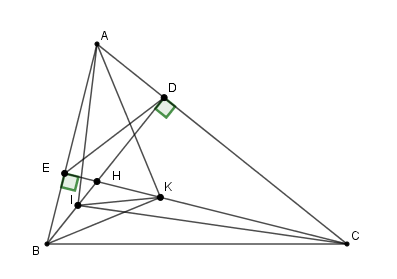
Xét \(\Delta AID\) và \(\Delta ACI\) có: \(\widehat {IAD}\) chung và \(\widehat {AIC} = \widehat {ADB} = {90^0}\) nên \(\Delta AID \backsim \Delta ACI\left( {g - g} \right)\)
Suy ra: \(\dfrac{{AI}}{{AC}} = \dfrac{{AD}}{{AI}} \Leftrightarrow A{I^2} = AC.AD\) (1)
Xét \(\Delta AEK\) và \(\Delta AKB\) có: \(\widehat {EAK}\) chung và \(\widehat {AIC} = \widehat {ADB} = {90^0}\) nên \(\Delta AEK \backsim \Delta AKB\left( {g - g} \right)\)
Suy ra: \(\dfrac{{AE}}{{AK}} = \dfrac{{AK}}{{AB}} \Leftrightarrow A{K^2} = AE.AB\) (2)
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)
\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\) \( \Rightarrow AE.{\rm{ }}AB = AC.{\rm{ }}AD\) (3)
Từ (1), (2) và (3) suy ra: \(A{I^2} = A{K^2} \Rightarrow AI = AK\) nên tam giác \(AIK\) cân tại \(A.\)
Cho \(\widehat {{\rm{AED}}} = {40^0}\). Tính số đo \(\widehat {{\rm{HBC}}}\).
-
A.
\(\widehat {{\rm{HBC}}} = {60^0}\)
-
B.
\(\widehat {{\rm{HBC}}} = {50^0}\)
-
C.
\(\widehat {{\rm{HBC}}} = {40^0}\)
-
D.
\(\widehat {{\rm{HBC}}} = {35^0}\)
Đáp án: B
Chứng minh \(\Delta ADE \backsim \Delta ABC\), sau đó suy ra các cặp góc tương ứng bằng nhau.
Từ đó sử dụng: Trong tam giác vuông, hai góc nhọn phụ nhau.
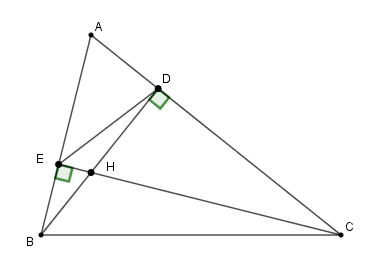
+) Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)
\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\) (g-g)
\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\)
Xét \(\Delta AED\) và \(\Delta ACB\) có: \(\widehat A\) chung và \(\dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\left( {cmt} \right)\) nên \(\Delta AED \backsim \Delta ACB\left( {c - g - c} \right)\)
Từ đó: \(\widehat {AED} = \widehat {ACB}\) (hai góc tương ứng)
Nên \(\widehat {ACB} = {40^0}\). Lại có: \(\Delta DBC\) vuông tại \(D\) nên \(\widehat {DCB} + \widehat {DBC} = {90^0}\)\( \Rightarrow \widehat {DBC} = {90^0} - {40^0} = {50^0}\)
Hay \(\widehat {HBC} = {50^0}\).
Hệ thức nào dưới đây đúng?
-
A.
\(BH.BD + CH.CE = A{B^2}\)
-
B.
\(BH.BD + CH.CE = A{C^2}\)
-
C.
\(BH.BD + CH.CE = 2B{C^2}\)
-
D.
\(BH.BD + CH.CE = B{C^2}\)
Đáp án: D
Kẻ \(AH\) cắt \(BC\) tại \(N.\)
Chứng minh các cặp tam giác đồng dạng \(\Delta BHN \backsim \Delta BCD;\,\Delta CHN \backsim \Delta CBE\) để suy ra các hệ thức đúng về cạnh.
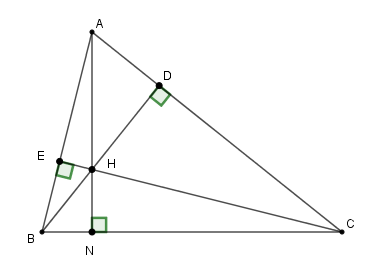
Kẻ \(AH\) cắt \(BC\) tại \(N.\) Vì \(H\) là giao điểm hai đường cao \(BD,CE\) nên \(H\) là trực tâm tam giác \(ABC.\)
Suy ra: \(AH \bot BC\) hay \(AN \bot BC.\)
Xét \(\Delta BHN\) và \(\Delta BCD\) có: \(\widehat B\) chung và \(\widehat {HNB} = \widehat {BDC} = {90^0}\) nên \(\Delta BHN \backsim \Delta BCD \left( {g - g} \right)\)
Suy ra: \(\dfrac{{BH}}{{BC}} = \dfrac{{BN}}{{BD}} \Rightarrow BH.BD = BN.BC\) (1)
Xét \(\Delta CHN\) và \(\Delta CBE\) có: \(\widehat C\) chung và \(\widehat {HNC} = \widehat {BEC} = {90^0}\) nên \(\Delta CHN \backsim \Delta CBE \left( {g - g} \right)\)
Suy ra: \(\dfrac{{CH}}{{CB}} = \dfrac{{CN}}{{CE}} \Rightarrow CH.CE = CN.BC\) (2)
Từ (1) và (2) suy ra \(BH.BD + CH.CE = BN.BC + CN.BC\)\( = BC\left( {CN + BN} \right) = BC.BC = B{C^2}\).
Vậy \(BH.BD + CH.CE = B{C^2}.\)
Tích \(AE{\rm{ }}.{\rm{ }}AB\;\) bằng:
-
A.
\(AC.AD\)
-
B.
\(AH.AC\)
-
C.
\(A{B^2}\)
-
D.
\(AH.AD\)
Đáp án: A
Sử dụng trường hợp đồng dạng thứ ba góc - góc rồi suy ra hệ thức tương ứng về cạnh.
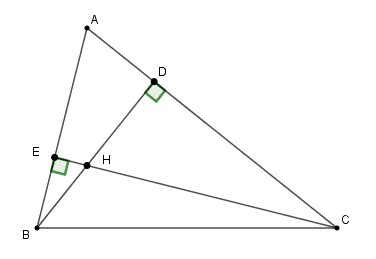
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)
\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\) (g-g)
\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\)\( \Rightarrow AE.{\rm{ }}AB = AC. {\rm{ }}AD\).
Cho \(a,b,c > 0\) thỏa mãn: \(6a + 2b + 3c = 11.\) Tìm giá trị nhỏ nhất của biểu thức \(M = \dfrac{{2b + 3c + 16}}{{1 + 6a}} + \dfrac{{6a + 3c + 16}}{{1 + 2b}} + \dfrac{{6a + 2b + 16}}{{1 + 3c}}\).
-
A.
\(8\)
-
B.
\(9\)
-
C.
\(15\)
-
D.
\(11\)
Đáp án : C
Biến đổi để sử dụng bất đẳng thức \(\dfrac{a}{b} + \dfrac{b}{a} \ge 2\) với \(a,b > 0\).
Dấu “=” xảy ra khi \(a = b.\)
Đặt \(x = 1 + 6a; y = 1 + 2b; z = 1 + 3c\,\,\left( {x,y,z > 0} \right)\)
\( \Rightarrow x + y + z = 1 + 6a + 1 + 2b + 1 + 3c\)\( = 3 + \left( {6a + 2b + 3c} \right) = 3 + 11 = 14\)
Ta có: \(2b + 3c + 16 = y - 1 + z - 1 + 16 = y + z + 14\)
\(6a + 3c + 16 = x + z + 14\)
\(6a + 2b + 16 = x + y + 14\)
Từ đó: \(M = \dfrac{{z + y + 14}}{x} + \dfrac{{x + z + 14}}{y} + \dfrac{{x + y + 14}}{z}\)
\( = \dfrac{z}{x} + \dfrac{y}{x} + \dfrac{{14}}{x} + \dfrac{x}{y} + \dfrac{z}{y} + \dfrac{{14}}{y} + \dfrac{x}{z} + \dfrac{y}{z} + \dfrac{{14}}{z}\)
\( = \left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + \left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + \left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + 14\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\)
\( = \left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + \left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + \left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + \left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\)
\( = 2\left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + 2\left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + 2\left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + 3\)
Mặt khác: \(\dfrac{x}{y} + \dfrac{y}{x} \ge 2\) dấu “ = ” xảy ra khi và chỉ khi \(x = y\)
\(\dfrac{x}{z} + \dfrac{z}{x} \ge 2.\) Dấu “ = ” xảy ra khi và chỉ khi \(x = z\)
\(\dfrac{z}{y} + \dfrac{y}{z} \ge 2.\) Dấu “ = ” xảy ra khi và chỉ khi \(z = y\)
Khi đó: \(M \ge 2. 2 + 2. 2 + 2. 2 + 3 \Rightarrow M \ge 15.\) Dấu “ = ” xảy ra khi và chỉ khi \(x = y = z = 1\)
Suy ra: \(a = \dfrac{{11}}{{18}};b = \dfrac{{11}}{6};c = \dfrac{{11}}{9}.\)
Vậy \({M_{min}} = 15\) khi \(a = \dfrac{{11}}{{18}};b = \dfrac{{11}}{6};c = \dfrac{{11}}{9}.\)
Luyện tập và củng cố kiến thức Đề thi khảo sát chất lượng đầu năm - Đề số 2 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Đề thi khảo sát chất lượng đầu năm - Đề số 3 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Đề thi khảo sát chất lượng đầu năm - Đề số 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Đề thi khảo sát chất lượng đầu năm - Đề số 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9
