-
Khảo sát chất lượng đầu năm
-
Chương 1 Căn bậc hai - Căn bậc ba
-
Chương 2 Hàm số bậc nhất
-
Chương 3 Hệ hai phương trình bậc nhất hai ẩn
- Bài 1: Phương trình bậc nhất hai ẩn
- Bài 2: Hệ hai phương trình bậc nhất hai ẩn
- Bài 3: Giải hệ phương trình bằng phương pháp thế
- Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
- Hệ phương trình bậc nhất hai ẩn chứa tham số
- Bài 5,6: Giải bài toán bằng cách lập hệ phương trình
- Bài tập hay và khó chương 3 về hệ phương trình
- Bài tập ôn tập chương 3
-
Chương 4 Hàm số y=ax^2. Phương trình bậc hai một ẩn
- Bài 1,2: Hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2
- Bài 3,4: Phương trình bậc hai một ẩn và công thức nghiệm
- Bài 5: Công thức nghiệm thu gọn
- Bài 6: Hệ thức Vi-ét và ứng dụng
- Bài 7: Phương trình quy về phương trình bậc hai
- Sự tương giao giữa đường thẳng và Parabol
- Bài 8: Giải bài toán bằng cách lập phương trình
- Hệ phương trình đối xứng
- Bài tập hay và khó chương 4: Sự tương giao của đường thẳng và parabol
- Tổng hợp câu hay và khó về giải bài toán bằng cách lập phương trình, hệ phương trình
- Tổng hợp câu hay và khó về hệ thức Vi-et
- Bài tập ôn tập chương 4
-
Chương 5 Hệ thức lượng trong tam giác vuông
-
Chương 6 Đường tròn
- Sự xác định của đường tròn- Tính chất đối xứng của đường tròn
- Bài 2: Đường kính và dây của đường tròn
- Bài 4: Vị trí tương đối giữa đường thẳng và đường tròn
- Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6: Tính chất hai tiếp tuyến cắt nhau
- Bài 7,8: Vị trí tương đối của hai đường tròn
- Bài tập hay và khó chương đường tròn
- Bài tập ôn tập chương 6
-
Chương 7 Góc với đường tròn
- Bài 1: Góc ở tâm- Số đo cung
- Bài 2: Liên hệ giữa cung và dây
- Bài 3: Góc nội tiếp
- Bài 4: Góc tạo bởi tiếp tuyến và dây cung
- Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn
- Bài 6: Cung chứa góc
- Bài 7: Tứ giác nội tiếp
- Bài 8: Đường tròn ngoại tiếp, đường tròn nội tiếp
- Bài 9: Độ dài đường tròn, cung tròn
- Bài 10: Diện tích hình tròn, quạt tròn
- Bài tập hay và khó chương góc với đường tròn
- Bài tập vận dụng cao từ các đề thi chuyên
- Bài tập ôn tập chương 7
-
Chương 8 Hình trụ - hình nón - hình cầu
Trắc nghiệm Bài 9: Độ dài đường tròn, cung tròn Toán 9
Đề bài
Số đo \(n^\circ \) của cung tròn có độ dài \(30,8\,cm\) trên đường tròn có bán kính \(22\,cm\) là ( lấy \(\pi \approx 3,14\) và làm tròn đến độ)
-
A.
$70^\circ $
-
B.
$80^\circ $
-
C.
$65^\circ $
-
D.
$85^\circ $
Tính độ dài cung \(30^\circ \) của một đường tròn có bán kính \(4\,dm\)
-
A.
$\dfrac{{4\pi }}{3}(dm)$
-
B.
$\dfrac{\pi }{3}(dm)$
-
C.
$\dfrac{\pi }{6}(dm)$
-
D.
$\dfrac{{2\pi }}{3}(dm)$
Chu vi đường tròn bán kính \(R = 9\) là
-
A.
$18\pi $
-
B.
$9\pi $
-
C.
$12\pi $
-
D.
$27\pi $
Biêt chu vi đường tròn là \(C = 36\pi (cm)\). Tính đường kính của đường tròn.
-
A.
$18(cm)$
-
B.
$14(cm)$
-
C.
$36(cm)$
-
D.
$20 (cm)$
Cho ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$ . Chọn khẳng định nào sau đây đúng?
-
A.
Độ dài nửa đường tròn đường kính $AC$ bằng hiệu các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$
-
B.
Độ dài nửa đường tròn đường kính $AC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$ .
-
C.
Độ dài nửa đường tròn đường kính $BC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $AC$
-
D.
Độ dài nửa đường tròn đường kính $AB$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AC$ và $BC$
Cho tam giác $ABC$ vuông tại $A$ , cạnh $AB = 5\,\,cm$ , \(\widehat B = {60^ \circ }\). Đường tròn tâm $I$ , đường kính $AB$ cắt $BC$ ở $D$ . Chọn khẳng định sai?
-
A.
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là $\dfrac{\pi }{6}\,\,\left( {cm} \right)$
-
B.
$AD \bot BC$
-
C.
$D$ thuộc đường tròn đường kính \(AC\)
-
D.
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là \(\dfrac{{5\pi }}{6}\,\,\left( {cm} \right)\)
Cho tam giác $ABC$ có \(AB = AC = 3\,\,cm,\,\,\widehat {\rm{A}} = {120^o}.\)Tính độ dài đường tròn ngoại tiếp tam giác $ABC$ .
-
A.
$12\pi $
-
B.
$9\pi $
-
C.
$6\pi $
-
D.
$3\pi $
Chu vi đường tròn ngoại tiếp tam giác đều cạnh \(a\,\left( {cm} \right)\) là
-
A.
$\dfrac{{4\pi a\sqrt 3 }}{3} (cm)$
-
B.
$\dfrac{{2\pi a\sqrt 3 }}{3} (cm)$
-
C.
$\dfrac{{\pi a\sqrt 3 }}{3} (cm)$
-
D.
$\dfrac{{5\pi a\sqrt 3 }}{3}(cm)$
Cho đường tròn $\left( O \right)$ bán kính $OA$ . Từ trung điểm $M$ của $OA$ vẽ dây\(BC \bot OA.\) Biết độ dài đường tròn $\left( O \right)$ là \(4\pi \,(cm).\) Độ dài cung lớn \(BC\) là
-
A.
$\dfrac{{4\pi }}{3}$
-
B.
$\dfrac{{5\pi }}{3}$
-
C.
$\dfrac{{7\pi }}{3}$
-
D.
$\dfrac{{8\pi }}{3}$
Cho đường tròn $(O; R)$ với dây cung $BC$ cố định. Điểm $A$ thuộc cung lớn $BC$. Đường phân giác của góc \(\widehat {BAC}\) cắt đường tròn $(O$) tại $D$. Các tiếp tuyến của đường tròn $(O; R)$ tại $C$ và $D$ cắt nhau tại $E$. Tia $CD$ cắt $AB$ tại $K$, đường thẳng $AD$ cắt $CE$ tại $I.$
Chọn khẳng định sai.
-
A.
\(BC{\rm{//}}DE\)
-
B.
$AKIC$ là tứ giác nội tiếp
-
C.
$AKIC$ không là tứ giác nội tiếp
-
D.
$OD \bot BC$
Cho \(BC = R\sqrt 3 .\)Tính theo $R$ độ dài cung nhỏ $BC$ của đường tròn (O; R).
-
A.
\(\dfrac{{2\pi R}}{3}\)
-
B.
$\dfrac{{5\pi R}}{3}$
-
C.
$\dfrac{{7\pi R}}{3}$
-
D.
$\dfrac{{4\pi R}}{3}$
Cho tam giác đều ABC nội tiếp đường tròn (O; R). Kẻ đường kính AD cắt BC tại H. Gọi M là một điểm trên cung nhỏ AC. Hạ \(BK \bot AM\) tại K. Đường thẳng BK cắt CM tại E. Tia BE cắt đường tròn (O; R) tại N (N khác B).
Chọn câu đúng. Tam giác MBE
-
A.
Cân tại \(M\)
-
B.
Vuông tại \(M\)
-
C.
Cân tại B
-
D.
Tam giác đều
Tính độ dài cung nhỏ MN theo R.
-
A.
\(\pi R\)
-
B.
\(\dfrac{{\pi R}}{2}\)
-
C.
\(\dfrac{{\pi R}}{3}\)
-
D.
\(\dfrac{{\pi R}}{4}\)
Lời giải và đáp án
Số đo \(n^\circ \) của cung tròn có độ dài \(30,8\,cm\) trên đường tròn có bán kính \(22\,cm\) là ( lấy \(\pi \approx 3,14\) và làm tròn đến độ)
-
A.
$70^\circ $
-
B.
$80^\circ $
-
C.
$65^\circ $
-
D.
$85^\circ $
Đáp án : B
Sử dụng công thức tính độ dài cung tròn:
Trên đường tròn bán kính$R$ , độ dài $l$ của một cung \(n^\circ \) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\,\).
Độ dài cung tròn \(l\) là:
\(l = \dfrac{{\pi Rn}}{{180}}\, \\ hay \;\dfrac{{\pi .22.n}}{{180}} = 30,8 \\ suy \; ra \; n \approx 80^\circ \).
Tính độ dài cung \(30^\circ \) của một đường tròn có bán kính \(4\,dm\)
-
A.
$\dfrac{{4\pi }}{3}(dm)$
-
B.
$\dfrac{\pi }{3}(dm)$
-
C.
$\dfrac{\pi }{6}(dm)$
-
D.
$\dfrac{{2\pi }}{3}(dm)$
Đáp án : D
Sử dụng công thức tính độ dài cung tròn:
Trên đường tròn bán kính$R$ , độ dài $l$ của một cung \(n^\circ \) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\,\).
Độ dài cung tròn \(l = \dfrac{{\pi Rn}}{{180}}\, = \dfrac{{\pi .4.30}}{{180}} = \dfrac{{2\pi }}{3} (dm)\).
Chu vi đường tròn bán kính \(R = 9\) là
-
A.
$18\pi $
-
B.
$9\pi $
-
C.
$12\pi $
-
D.
$27\pi $
Đáp án : A
Sử dụng công thức chu vi đường tròn bán kính \(R\) là \(C = 2\pi R\,\)
Chu vi \(C = 2\pi R = 2\pi .9 = 18\pi \).
Biêt chu vi đường tròn là \(C = 36\pi (cm)\). Tính đường kính của đường tròn.
-
A.
$18(cm)$
-
B.
$14(cm)$
-
C.
$36(cm)$
-
D.
$20 (cm)$
Đáp án : C
Sử dụng công thức chu vi đường tròn đường kính \(d = 2R\) là \(C = \pi d\,\)
Chu vi \(C = \pi d = 36\pi \) suy ra \( d = 36\). Vậy đường kính cần tìm là \(36(cm)\) .
Cho ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$ . Chọn khẳng định nào sau đây đúng?
-
A.
Độ dài nửa đường tròn đường kính $AC$ bằng hiệu các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$
-
B.
Độ dài nửa đường tròn đường kính $AC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$ .
-
C.
Độ dài nửa đường tròn đường kính $BC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $AC$
-
D.
Độ dài nửa đường tròn đường kính $AB$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AC$ và $BC$
Đáp án : B
Sử dụng công thức tính độ dài nửa đường tròn bán kính $R$ (nửa chu vi đường tròn):
\(l = \pi R\).
Độ dài nửa đường tròn đường kính \(AC\) là \({l_1} = \pi .\dfrac{{AC}}{2}\) .
Độ dài nửa đường tròn đường kính \(AB\) là \({l_1} = \pi .\dfrac{{AB}}{2}\) .
Độ dài nửa đường tròn đường kính \(BC\) là \({l_1} = \pi .\dfrac{{BC}}{2}\) .
Mà ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$ nên \(AB + BC = AC\)
Do đó \({l_1} = \pi .\dfrac{{AC}}{2} = \pi \left( {\dfrac{{AB}}{2} + \dfrac{{BC}}{2}} \right) = \pi .\dfrac{{AB}}{2} + \pi .\dfrac{{BC}}{2} = {l_2} + {l_3}\)
Vậy độ dài nửa đường tròn đường kính $AC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$ .
Cho tam giác $ABC$ vuông tại $A$ , cạnh $AB = 5\,\,cm$ , \(\widehat B = {60^ \circ }\). Đường tròn tâm $I$ , đường kính $AB$ cắt $BC$ ở $D$ . Chọn khẳng định sai?
-
A.
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là $\dfrac{\pi }{6}\,\,\left( {cm} \right)$
-
B.
$AD \bot BC$
-
C.
$D$ thuộc đường tròn đường kính \(AC\)
-
D.
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là \(\dfrac{{5\pi }}{6}\,\,\left( {cm} \right)\)
Đáp án : A
+ Sử dụng góc nội tiếp chắn nửa đường tròn bằng \(90^\circ \)
+ Sử dụng công thức tính độ dài cung tròn:
Trên đường tròn bán kính$R$ , độ dài $l$ của một cung \(n^\circ \) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\,\).
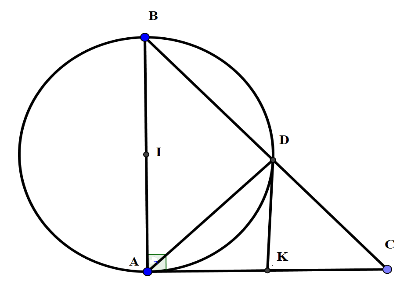
+ Xét đường tròn \(\left( I \right)\) đường kính \(AB\) có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên $AD \bot BC \Rightarrow $ phương án B đúng.
+) Gọi \(K\) là trung điểm của \(AC \Rightarrow KA = KC = KD \Rightarrow K\) đường tròn đường kính \(AC \Rightarrow \) phương án C đúng.
+) Ta có \(\Delta IBD\) cân tại \(I\) có \(\widehat B = 60^\circ \Rightarrow \Delta IBD\) đều nên \(\widehat {BID} = 60^\circ \)
Độ dài cung nhỏ \(BD\) của \(\left( I \right)\) là $l = \dfrac{{\pi .\dfrac{5}{2}.60}}{{180^\circ }} = \dfrac{{5\pi }}{6}\,\left( {cm} \right) \Rightarrow $ phương án D đúng.
Cho tam giác $ABC$ có \(AB = AC = 3\,\,cm,\,\,\widehat {\rm{A}} = {120^o}.\)Tính độ dài đường tròn ngoại tiếp tam giác $ABC$ .
-
A.
$12\pi $
-
B.
$9\pi $
-
C.
$6\pi $
-
D.
$3\pi $
Đáp án : C
Sử dụng công thức chu vi đường tròn bán kính \(R\) là \(C = 2\pi R\,\).
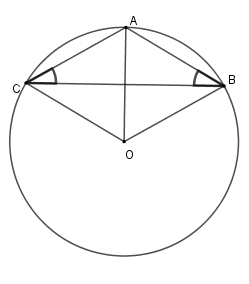
Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) . Vì tam giác \(ABC\) cân tại \(A\) nên \(AO\) vừa là đường cao vừa là phân giác của \(\widehat {BAC}\)
Suy ra \(\widehat {CAO} = \dfrac{{120^\circ }}{2} = 60^\circ \) . Xét tam giác \(CAO\) có \(OA = OC;\widehat {CAO} = 60^\circ \Rightarrow \Delta CAO\) đều nên \(OA = OC = AC = 3\,cm\) .
Nên bán kính đường tròn ngoại tiếp \(\Delta ABC\) là \(R = 3\,cm\)
Chu vi đường tròn \(\left( O \right)\) là \(C = 2\pi R = 6\pi \,\,\left( {cm} \right)\)
Chu vi đường tròn ngoại tiếp tam giác đều cạnh \(a\,\left( {cm} \right)\) là
-
A.
$\dfrac{{4\pi a\sqrt 3 }}{3} (cm)$
-
B.
$\dfrac{{2\pi a\sqrt 3 }}{3} (cm)$
-
C.
$\dfrac{{\pi a\sqrt 3 }}{3} (cm)$
-
D.
$\dfrac{{5\pi a\sqrt 3 }}{3}(cm)$
Đáp án : B
Sử dụng công thức chu vi đường tròn bán kính \(R\) là \(C = 2\pi R\,\)
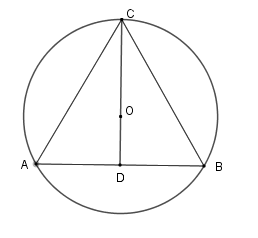
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác đều \(BAC\) , suy ra \(O\) cũng là trọng tâm của tam giác \(ABC\) .
Tia \(CO \bot AB\) tại \(D\) thì $D$ là trung điểm của \(AB\) \( \Rightarrow OC = \dfrac{2}{3}CD\)
Xét tam giác vuông \(ADC\) có \(AC = a\,;\,\widehat {CAD} = 60^\circ \Rightarrow CD = AC.\sin 60^\circ = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow OC = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Nên bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = \dfrac{{a\sqrt 3 }}{3} \Rightarrow C = 2\pi R = \dfrac{{2\pi a\sqrt 3 }}{3}\) .
Cho đường tròn $\left( O \right)$ bán kính $OA$ . Từ trung điểm $M$ của $OA$ vẽ dây\(BC \bot OA.\) Biết độ dài đường tròn $\left( O \right)$ là \(4\pi \,(cm).\) Độ dài cung lớn \(BC\) là
-
A.
$\dfrac{{4\pi }}{3}$
-
B.
$\dfrac{{5\pi }}{3}$
-
C.
$\dfrac{{7\pi }}{3}$
-
D.
$\dfrac{{8\pi }}{3}$
Đáp án : D
Bước 1: Tìm bán kính của đường tròn dựa vào công thức tính chu vi \(C = 2\pi R.\)
Bước 2: Sử dụng công thức tính độ dài cung tròn: \(l = \dfrac{{\pi Rn}}{{180}}.\)
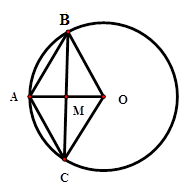
Vì độ dài đường tròn là \(4\pi \) nên $4\pi = 2\pi .R \Rightarrow R = 2\,cm$ (\(R\) là bán kính đường tròn)
Xét tứ giác \(ABOC\) có hai đường chéo \(AO \bot BC\) tại \(M\) là trung điểm mỗi đường nên tứ giác \(ABOC\) là hình thoi.
Suy ra \(OB = OC = AB \Rightarrow \Delta ABO\) đều \( \Rightarrow \widehat {AOB} = 60^\circ \Rightarrow \widehat {BOC} = 120^\circ \)
Suy ra số đo cung lớn \(BC\) là \(360^\circ - 120^\circ = 240^\circ \)
Độ dài cung lớn \(BC\) là \(l = \dfrac{{\pi .2.240}}{{180}} = \dfrac{{8\pi }}{3}\,\left( {cm} \right).\)
Cho đường tròn $(O; R)$ với dây cung $BC$ cố định. Điểm $A$ thuộc cung lớn $BC$. Đường phân giác của góc \(\widehat {BAC}\) cắt đường tròn $(O$) tại $D$. Các tiếp tuyến của đường tròn $(O; R)$ tại $C$ và $D$ cắt nhau tại $E$. Tia $CD$ cắt $AB$ tại $K$, đường thẳng $AD$ cắt $CE$ tại $I.$
Chọn khẳng định sai.
-
A.
\(BC{\rm{//}}DE\)
-
B.
$AKIC$ là tứ giác nội tiếp
-
C.
$AKIC$ không là tứ giác nội tiếp
-
D.
$OD \bot BC$
Đáp án: C
Sử dụng các kiến thức về liên hệ giữa đường kính và dây cung, góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung, các dấu hiệu nhận biết tứ giác nội tiếp.
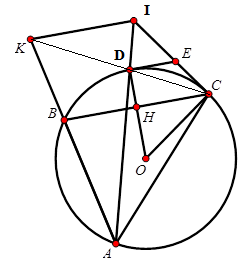
+ Vì \(AD\) là tia phân giác \(\widehat {BAC} \Rightarrow D\) là điểm chính giữa cung \(BC\) .
Nên \(OD \bot BC\) \( \Rightarrow \) phương án D đúng
+ Mà \(DE \bot OD\) (\(DE\) là tiếp tuyến của \(\left( O \right)\)) suy ra \(BC{\rm{//}}DE\) \( \Rightarrow \) phương án A đúng.
+) Xét \(\left( O \right)\) có \(\widehat {DAC} = \widehat {DCI}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung \(DC\) )
Mà \(\widehat {BAD} = \widehat {DAC}\) ($AD$ là phân giác) nên \(\widehat {KAI} = \widehat {KCI}\) nên tứ giác \(KICA\) nội tiếp \( \Rightarrow \) phương án B đúng.
Cho \(BC = R\sqrt 3 .\)Tính theo $R$ độ dài cung nhỏ $BC$ của đường tròn (O; R).
-
A.
\(\dfrac{{2\pi R}}{3}\)
-
B.
$\dfrac{{5\pi R}}{3}$
-
C.
$\dfrac{{7\pi R}}{3}$
-
D.
$\dfrac{{4\pi R}}{3}$
Đáp án: A
Bước 1: Tìm số đo cung bằng cách sử dụng tỉ số lượng giác của góc nhọn
Bước 2: Sử dụng công thức tính độ dài cung tròn:
Trên đường tròn bán kính$R$ , độ dài $l$ của một cung \(n^\circ \) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\,\).
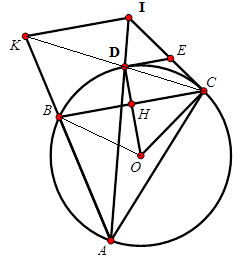
Gọi \(OD \cap BC\) tại \(H\) thì \(H\) là trung điểm \(BC\) (do \(OD \bot BC\) tại \(H\) )\( \Rightarrow HC = \dfrac{{BC}}{2} = \dfrac{{R\sqrt 3 }}{2}\)
Xét tam giác vuông \(HOC\) có \(\sin \widehat {HOC} = \dfrac{{HC}}{{OC}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {HOC} = 60^\circ \Rightarrow \widehat {BOC} = 120^\circ \)
Độ dài cung nhỏ \(BC\) là \(l = \dfrac{{\pi .R.120}}{{180}} = \dfrac{{2\pi R}}{3}\) \(\left( {cm} \right)\) .
Cho tam giác đều ABC nội tiếp đường tròn (O; R). Kẻ đường kính AD cắt BC tại H. Gọi M là một điểm trên cung nhỏ AC. Hạ \(BK \bot AM\) tại K. Đường thẳng BK cắt CM tại E. Tia BE cắt đường tròn (O; R) tại N (N khác B).
Chọn câu đúng. Tam giác MBE
-
A.
Cân tại \(M\)
-
B.
Vuông tại \(M\)
-
C.
Cân tại B
-
D.
Tam giác đều
Đáp án: A
Chứng minh tam giác \(MBE\) có hai góc ở đáy bằng nhau
Sử dụng:
+ Số đo góc nội tiếp bằng nửa số đo cung bị chắn
+ Góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn
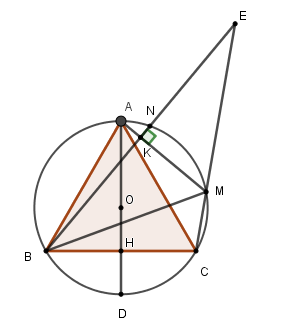
Xét đường tròn \(\left( O \right)\) có tam giác \(ABC\) đều nên sđ \(AB = sd\,AC = sd\,BC = \dfrac{{360^\circ }}{3} = 120^\circ \)
\(\widehat {AMB}\) là góc nội tiếp chắn cung \(AB \Rightarrow \widehat {AMB} = \dfrac{1}{2}sd\,AB = \dfrac{{120^\circ }}{2} = 60^\circ \)
Suy ra \(\widehat {KBM} = 90^\circ - \widehat {KMB} = 90^\circ - 60^\circ = 30^\circ \) suy ra \(sd\,NM = 2.\widehat {NBM} = 2.30^\circ = 60^\circ \)
\(\widehat {NBM} = 30^\circ \left( {cmt} \right)\) và \(\widehat {BEM} = \dfrac{1}{2}\left( {sd\,BC - sd\,NM} \right) = \dfrac{1}{2}\left( {120^\circ - 60^\circ } \right) = 30^\circ \) nên tam giác \(MBE\) cân tại \(M.\)
Tính độ dài cung nhỏ MN theo R.
-
A.
\(\pi R\)
-
B.
\(\dfrac{{\pi R}}{2}\)
-
C.
\(\dfrac{{\pi R}}{3}\)
-
D.
\(\dfrac{{\pi R}}{4}\)
Đáp án: C
Cung tròn có bán kính \(R\) và số đo \(n^\circ \) thì có độ dài \(l = \dfrac{{\pi Rn}}{{180}}.\)
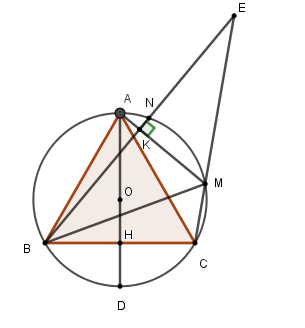
Độ dài cung \(NM\) là \(l = \dfrac{{\pi R.60}}{{180}} = \dfrac{{\pi R}}{3}.\)
Luyện tập và củng cố kiến thức Bài 10: Diện tích hình tròn, quạt tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập hay và khó chương góc với đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập vận dụng cao từ các đề thi chuyên Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 7 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Đường tròn ngoại tiếp, đường tròn nội tiếp Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7: Tứ giác nội tiếp Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6: Cung chứa góc Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Góc tạo bởi tiếp tuyến và dây cung Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Góc nội tiếp Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Liên hệ giữa cung và dây Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Góc ở tâm- Số đo cung Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9
