Trắc nghiệm Bài 4: Vị trí tương đối giữa đường thẳng và đường tròn Toán 9
Đề bài
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Nếu đường thẳng và đường tròn có duy nhất một điểm chung thì
-
A.
đường thẳng tiếp xúc với đường tròn
-
B.
đường thẳng cắt đường tròn
-
C.
đường thẳng không cắt đường tròn
-
D.
đáp án khác
Nếu đường thẳng $d$ là tiếp tuyến của đường tròn $\left( O \right)$ tại $A$ thì
-
A.
$d{\rm{//}}OA$
-
B.
$d \equiv OA$
-
C.
$d \bot OA$ tại$A$
-
D.
$d \bot OA$ tại $O$
Cho đường tròn $\left( O \right)$ và đường thẳng $a$. Kẻ $OH \bot a$ tại $H$, biết $OH > R$ khi đó đường thẳng $a$ và đường tròn $\left( O \right)$
-
A.
cắt nhau
-
B.
không cắt nhau
-
C.
tiếp xúc
-
D.
đáp án khác
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |
-
A.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
B.
$\left( 1 \right)$ : $9\,cm$; $\left( 2 \right)$ : cắt nhau
-
C.
$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
D.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $6\,cm$
Cho hai đường tròn \(\left( {O;4cm} \right)\) và \(\left( {O';3cm} \right)\) biết \(OO' = 5cm\). Hai đường tròn trên cắt nhau tại \(A\) và \(B\). Độ dài \(AB\) là:
-
A.
\(2,4cm\)
-
B.
\(4,8cm\)
-
C.
\(\dfrac{5}{{12}}cm\)
-
D.
\(5cm\)
Đường thẳng \(a\) cách tâm \(O\) của đường tròn \(\left( {O;R} \right)\)một khoảng bằng \(\sqrt 8 \,\,cm.\) Biết \(R = 3\,\,cm,\) số giao điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) là:
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(3\).
Trên mặt phẳng tọa độ $Oxy$, cho điểm $A\left( {4;5} \right)$. Hãy xác định vị trí tương đối của đường tròn $\left( {A;5} \right)$ và các trục tọa độ.
-
A.
Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
-
B.
Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn
-
C.
Cả hai trục tọa độ đều cắt đường tròn
-
D.
Cả hai trục tọa độ đều tiếp xúc với đường tròn.
Cho $a,b$ là hai đường thẳng song song và cách nhau một khoảng $2,5\,cm$. Lấy điểm $I$ trên $a$ và vẽ đường tròn $\left( {I;2,5cm} \right)$. Khi đó đường tròn với đường thẳng $b$
-
A.
cắt nhau
-
B.
không cắt nhau
-
C.
tiếp xúc
-
D.
đáp án khác
Cho góc $\widehat {xOy}\,\left( {0 < \widehat {xOy} < 180^\circ } \right)$. Đường tròn $\left( I \right)$ là đường tròn tiếp xúc với cả hai cạnh $Ox;Oy$. Khi đó điểm $I$ chạy trên đường nào?
-
A.
Đường thẳng vuông góc với $Ox$ tại $O$
-
B.
Tia phân giác của góc $\widehat {xOy}$
-
C.
Tia $Oz$ nằm giữa $Ox$ và $Oy$
-
D.
Tia phân giác của góc $\widehat {xOy}$ trừ điểm $O$
Cho đường tròn tâm $O$ bán kính $3cm$ và một điểm $A$ cách $O$ là $5cm$. Kẻ tiếp tuyến $AB$ với đường tròn ( $B$ là tiếp điểm). Tính độ dài $AB$.
-
A.
$AB = \,3\,cm$
-
B.
$AB = \,4\,cm$
-
C.
$AB = \,5\,cm$
-
D.
$AB = \,2\,cm$
Cho đường tròn $\left( {O;R} \right)$ và dây $AB = 1,2R$. Vẽ một tiếp tuyến song song với $AB$, cắt các tia $OA,OB$ lần lượt tại $E$ và $F$. Tính diện tích tam giác $OEF$ theo $R$.
-
A.
${S_{OEF}} = 0,75{R^2}$
-
B.
${S_{OEF}} = 1,5{R^2}$
-
C.
${S_{OEF}} = 0,8{R^2}$
-
D.
${S_{OEF}} = 1,75{R^2}$
Cho đường tròn $(O;R)$. Cát tuyến qua $A$ ở ngoài $(O)$ cắt $(O)$ tại $B$ và $C$. Cho biết $AB = BC$ và kẻ đường kính $COD$. Tính độ dài đoạn thẳng $AD.$
-
A.
$AD = R$
-
B.
$AD = 3R$
-
C.
$AD = \dfrac{R}{2}$
-
D.
$AD = 2R$
Cho hai đường thẳng $a$ và $b$ song song với nhau, cách nhau một khoảng là $h$. Một đường tròn $\left( O \right)$ tiếp xúc với $a$ và $b$. Hỏi tâm $O$ di động trên đường nào?
-
A.
Đường thẳng $c$ song song và cách đều $a,b$ một khoảng $\dfrac{h}{2}$.
-
B.
Đường thẳng $c$ song song và cách đều $a,b$ một khoảng $\dfrac{{2h}}{3}$.
-
C.
Đường thẳng $c$ đi qua $O$ vuông góc với $a,b$
-
D.
Đường tròn $\left( {A;AB} \right)$ với $A,B$ lần lượt là tiếp điểm của $a,b$ với $\left( O \right)$.
Cho đường tròn (O; R) đường kính AB. Vẽ các tia tiếp tuyến Ax, By với nửa đường tròn. Lấy điểm M di động trên tía Ax, điểm N di động trên tia Oy sao cho \(AM.BN = {R^2}.\)
Chọn câu đúng:
-
A.
MN là tiếp tuyến của đường tròn (O)
-
B.
\(\widehat {MON} = 90^\circ \)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
Chọn câu đúng.
-
A.
Đường tròn ngoại tiếp tam giác OMN luôn tiếp xúc với đường thẳng AB cố định.
-
B.
Đường tròn ngoại tiếp tam giác OMN luôn tiếp xúc với đường thẳng AM cố định
-
C.
Đường tròn ngoại tiếp tam giác OMN luôn tiếp xúc với đường thẳng BN cố định
-
D.
Cả A, B, C đều sai
Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Trên AO lấy điểm M sao cho \(AM = AB.\) Các tia BM và CM lần lượt cắt đường tròn tại một điểm thứ hai là D và E. Chọn câu đúng.
-
A.
M là tâm đường tròn ngoại tiếp tam giác OBC
-
B.
DE là đường kính của đường tròn (O)
-
C.
M là tâm đường tròn nội tiếp tam giác OBC
-
D.
Cả A, B, C đều sai
Lời giải và đáp án
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : B
Đường thẳng và đường tròn có nhiều nhất hai điểm chung.
Nếu đường thẳng và đường tròn có duy nhất một điểm chung thì
-
A.
đường thẳng tiếp xúc với đường tròn
-
B.
đường thẳng cắt đường tròn
-
C.
đường thẳng không cắt đường tròn
-
D.
đáp án khác
Đáp án : A
|
Vị trí tương đối của đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa $d$ và $R$ |
|
Đường thẳng và đường tròn cắt nhau |
$R$ |
$d < R$ |
|
Đường thẳng và đường tròn tiếp xúc nhau |
$1$ |
$d = R$ |
|
Đường thẳng và đường tròn không giao nhau |
$0$ |
$d > R$ |
Đường thẳng và đường tròn chỉ có một điểm chung thì đường thẳng tiếp xúc với đường tròn.
Nếu đường thẳng $d$ là tiếp tuyến của đường tròn $\left( O \right)$ tại $A$ thì
-
A.
$d{\rm{//}}OA$
-
B.
$d \equiv OA$
-
C.
$d \bot OA$ tại$A$
-
D.
$d \bot OA$ tại $O$
Đáp án : C
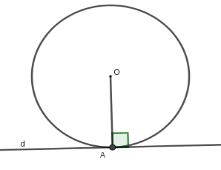
Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
Nên $d \bot OA$ tại tiếp điểm $A$.
Cho đường tròn $\left( O \right)$ và đường thẳng $a$. Kẻ $OH \bot a$ tại $H$, biết $OH > R$ khi đó đường thẳng $a$ và đường tròn $\left( O \right)$
-
A.
cắt nhau
-
B.
không cắt nhau
-
C.
tiếp xúc
-
D.
đáp án khác
Đáp án : B
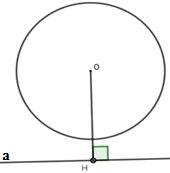
Vì $OH > R$ nên a không cắt $\left( O \right).$
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |
-
A.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
B.
$\left( 1 \right)$ : $9\,cm$; $\left( 2 \right)$ : cắt nhau
-
C.
$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
D.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $6\,cm$
Đáp án : A
Sử dụng bảng vị trí tương đối của đường thẳng và đường tròn
|
Vị trí tương đối của đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa $d$ và $R$ |
|
Đường thẳng và đường tròn cắt nhau |
$2$ |
$d < R$ |
|
Đường thẳng và đường tròn tiếp xúc nhau |
$1$ |
$d = R$ |
|
Đường thẳng và đường tròn không giao nhau |
$0$ |
$d > R$ |
+) Vì $d < R\left( {4cm < 5cm} \right)$ nên đường thẳng cắt đường tròn
+) Vì đường thẳng tiếp xúc với đường tròn nên $d = R = 8\,cm$
Cho hai đường tròn \(\left( {O;4cm} \right)\) và \(\left( {O';3cm} \right)\) biết \(OO' = 5cm\). Hai đường tròn trên cắt nhau tại \(A\) và \(B\). Độ dài \(AB\) là:
-
A.
\(2,4cm\)
-
B.
\(4,8cm\)
-
C.
\(\dfrac{5}{{12}}cm\)
-
D.
\(5cm\)
Đáp án : B
Dựa vào tính chất hai đường tròn cắt nhau.
Định lí Pi-ta-go đảo.
Hệ thức lượng trong tam giác vuông.
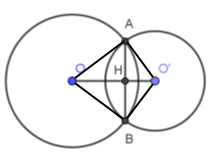
Gọi giao điểm của AB và OO' là H. Khi đó AB vuông góc với OO' tại H.
Xét tam giác \(OAO'\) có \(O{A^2} + O'{A^2} = OO{'^2}\) (vì \({4^2} + {3^2} = {5^2}\)) nên tam giác \(OAO'\) vuông tại \(A\).
Xét tam giác \(OAO'\) có \(AH\) là đường cao nên \(AH.OO' = OA.O'A \Rightarrow AH = \dfrac{{OA.O'A}}{{OO'}} = \dfrac{{4.3}}{5} = \dfrac{{12}}{5}\)
Mà \(AB = 2AH\) nên \(AB = \dfrac{{24}}{5} = 4,8cm\)
Đường thẳng \(a\) cách tâm \(O\) của đường tròn \(\left( {O;R} \right)\)một khoảng bằng \(\sqrt 8 \,\,cm.\) Biết \(R = 3\,\,cm,\) số giao điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) là:
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(3\).
Đáp án : C
Vị trí tương đối của đường tròn tâm \(O\) bán kính \(R\) và đường thẳng \(a\):
+) Nếu \(d\left( {O;\,\,a} \right) < R \) thì \(a\) cắt đường tròn tại hai điểm phân biệt.
+) Nếu \(d\left( {O;\,\,a} \right) = R \) thì \(a\) tiếp xúc với đường tròn tại 1 điểm.
+) Nếu \(d\left( {O;\,\,a} \right) > R \) thì \(a\) không cắt đường tròn.
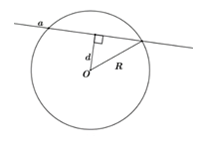 Ta có: \(d\left( {O;\,\,a} \right) = \sqrt 8 ;\,\,\,\,R = 3 \) suy ra \( d\left( {O;\,\,a} \right) < R\)
Ta có: \(d\left( {O;\,\,a} \right) = \sqrt 8 ;\,\,\,\,R = 3 \) suy ra \( d\left( {O;\,\,a} \right) < R\)
Nên đường thẳng \(a\) cắt đường tròn \(\left( {O;\,\,R} \right)\) tại hai điểm phân biệt.
Trên mặt phẳng tọa độ $Oxy$, cho điểm $A\left( {4;5} \right)$. Hãy xác định vị trí tương đối của đường tròn $\left( {A;5} \right)$ và các trục tọa độ.
-
A.
Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
-
B.
Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn
-
C.
Cả hai trục tọa độ đều cắt đường tròn
-
D.
Cả hai trục tọa độ đều tiếp xúc với đường tròn.
Đáp án : A
Bước 1: Xác định khoảng cách từ tâm $A$ đến các trục tọa độ.
Bước 2: Sử dụng vị trí tương đối giữa đường thẳng và đường tròn.
Vì $A\left( {4;5} \right)$ nên khoảng cách từ $A$ đến trục hoành là ${d_1} = \left| {{y_A}} \right| = 5$, khoảng cách từ $A$ đến trục tung là ${d_2} = \left| {{x_A}} \right| = 4$
Nhận thấy ${d_2} = R\left( { = 5} \right)$ nên trục hoành tiếp xúc với đường tròn $\left( {A;5} \right)$.
Và ${d_2} = 4 < 5 = R$ nên trục tung cắt đường tròn $\left( {A;5} \right)$.
Cho $a,b$ là hai đường thẳng song song và cách nhau một khoảng $2,5\,cm$. Lấy điểm $I$ trên $a$ và vẽ đường tròn $\left( {I;2,5cm} \right)$. Khi đó đường tròn với đường thẳng $b$
-
A.
cắt nhau
-
B.
không cắt nhau
-
C.
tiếp xúc
-
D.
đáp án khác
Đáp án : C
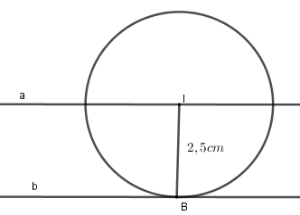
Vì hai đường thẳng song song $a,b$ cách nhau một khoảng là $2,5\,cm$ mà $I \in a$ nên khoảng cách từ tâm $I$ đến đường thẳng $b$ là $d = 2,5\,cm$.
Suy ra $d = R = 2,5\,cm$ nên đường tròn $\left( {I;2,5cm} \right)$ và đường thẳng $b$ tiếp xúc với nhau.
Cho góc $\widehat {xOy}\,\left( {0 < \widehat {xOy} < 180^\circ } \right)$. Đường tròn $\left( I \right)$ là đường tròn tiếp xúc với cả hai cạnh $Ox;Oy$. Khi đó điểm $I$ chạy trên đường nào?
-
A.
Đường thẳng vuông góc với $Ox$ tại $O$
-
B.
Tia phân giác của góc $\widehat {xOy}$
-
C.
Tia $Oz$ nằm giữa $Ox$ và $Oy$
-
D.
Tia phân giác của góc $\widehat {xOy}$ trừ điểm $O$
Đáp án : D
Xác định xem tâm đường tròn cách đường thẳng cho trước một khoảng bằng bao nhiêu rồi sử dụng tính chất tia phân giác của một góc để xác định tập hợp điểm.
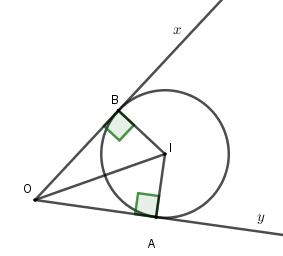
Kẻ $IA \bot Oy;IB \bot Ox$ tại $A,B$.
Vì $\left( I \right)$ tiếp xúc với cả $Ox;Oy$ nên $IA = IB$ suy ra $I$ thuộc tia phân giác của góc $\widehat {xOy}$ ($I \ne O$)
(tính chất tia phân giác của một góc)
Cho đường tròn tâm $O$ bán kính $3cm$ và một điểm $A$ cách $O$ là $5cm$. Kẻ tiếp tuyến $AB$ với đường tròn ( $B$ là tiếp điểm). Tính độ dài $AB$.
-
A.
$AB = \,3\,cm$
-
B.
$AB = \,4\,cm$
-
C.
$AB = \,5\,cm$
-
D.
$AB = \,2\,cm$
Đáp án : B
Sử dụng định lý về tiếp tuyến của đường tròn và định lý Pytago để tính toán
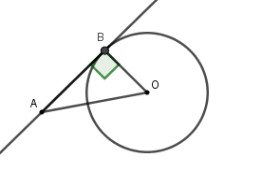
Vì $AB$ là tiếp tuyến và $B$ là tiếp điểm nên $OB = R = 3\,cm$; $AB \bot OB$ tại $B$.
Áp dụng định lý Pytago cho tam giác $ABO$ vuông tại $B$ ta được $AB = \sqrt {O{A^2} - O{B^2}} = \sqrt {{5^2} - {3^2}} = 4\,cm$
Vậy $AB = \,4\,cm$.
Cho đường tròn $\left( {O;R} \right)$ và dây $AB = 1,2R$. Vẽ một tiếp tuyến song song với $AB$, cắt các tia $OA,OB$ lần lượt tại $E$ và $F$. Tính diện tích tam giác $OEF$ theo $R$.
-
A.
${S_{OEF}} = 0,75{R^2}$
-
B.
${S_{OEF}} = 1,5{R^2}$
-
C.
${S_{OEF}} = 0,8{R^2}$
-
D.
${S_{OEF}} = 1,75{R^2}$
Đáp án : A
Sử dụng định lý về tiếp tuyến của đường tròn, liên hệ giữa đường kính và dây, định lý Pytago để tính toán.
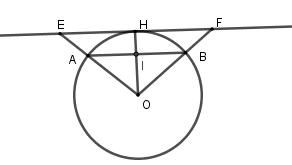
Kẻ $OH \bot EF$ tại $H$ và cắt $AB$ tại $I$ suy ra $OI \bot AB$ ( vì $AB{\rm{//}}EF$)
Xét $\left( O \right)$ có $OI \bot AB$ tại $I$ nên $I$ là trung điểm của $AB$ (liên hệ giữa đường kính và dây)
$ \Rightarrow IA = IB = \dfrac{{AB}}{2} = 0,6R$. Lại có $OA = R$.
Áp dụng định lý Pytago cho tam giác vuông $OIA$ ta có $OI = \sqrt {O{A^2} - I{A^2}} = 0,8R$.
Mà $AI\,{\rm{//}}\,EH$ nên $\dfrac{{AI}}{{EH}} = \dfrac{{OI}}{{OH}} = \dfrac{{0,8R}}{R} \Rightarrow EH = \dfrac{{0,6R}}{{0,8}} = 0,75R$
$\Delta OEF$cân tại $O$ (vì $\widehat E = \widehat F = \widehat {BAO} = \widehat {ABO}$) có $OH \bot EF$ nên $H$ là trung điểm của $EF$
$ \Rightarrow EF = 2EH = 1,5R$$ \Rightarrow {S_{EOF}} = \dfrac{{OH.EF}}{2} = 0,75{R^2}$.
Cho đường tròn $(O;R)$. Cát tuyến qua $A$ ở ngoài $(O)$ cắt $(O)$ tại $B$ và $C$. Cho biết $AB = BC$ và kẻ đường kính $COD$. Tính độ dài đoạn thẳng $AD.$
-
A.
$AD = R$
-
B.
$AD = 3R$
-
C.
$AD = \dfrac{R}{2}$
-
D.
$AD = 2R$
Đáp án : D
+) Nhắc lại : Cát tuyến là đường thẳng cắt đường tròn tại hai điểm.
+) Sử dụng Pytago để tính toán.
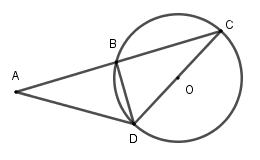
Xét $\left( O \right)$ có $OB = OC = OD$$ \Rightarrow BO = \dfrac{{DC}}{2}$$ \Rightarrow \Delta BDC$ vuông tại $B$ (tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông)
Suy ra $BD \bot AC$.
Xét $\Delta ADC$ có $BD$ vừa là đường trung tuyến vừa là đường cao nên $\Delta ADC$ cân tại $D \Rightarrow DA = DC = 2R$
Vậy $AD = 2R.$
Cho hai đường thẳng $a$ và $b$ song song với nhau, cách nhau một khoảng là $h$. Một đường tròn $\left( O \right)$ tiếp xúc với $a$ và $b$. Hỏi tâm $O$ di động trên đường nào?
-
A.
Đường thẳng $c$ song song và cách đều $a,b$ một khoảng $\dfrac{h}{2}$.
-
B.
Đường thẳng $c$ song song và cách đều $a,b$ một khoảng $\dfrac{{2h}}{3}$.
-
C.
Đường thẳng $c$ đi qua $O$ vuông góc với $a,b$
-
D.
Đường tròn $\left( {A;AB} \right)$ với $A,B$ lần lượt là tiếp điểm của $a,b$ với $\left( O \right)$.
Đáp án : A
Xác định xem tâm đường tròn cách đường thẳng cho trước một khoảng bằng bao nhiêu rồi sử dụng tính chất điểm cách đều đường thẳng để xác định quỹ tích.
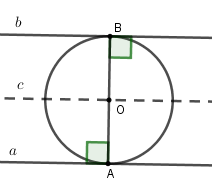
Kẻ đường thẳng $OA \bot a$ tại $A$ cắt $b$ tại $B$ thì $OB \bot b$ tại $B$ vì $a{\rm{//}}b$.
Vì $\left( O \right)$ tiếp xúc với cả $a,b$ nên $OA = OB$. Lại có $AB = h \Rightarrow OA = OB = \dfrac{h}{2}$
Hay tâm $O$ cách $a$ và $b$ một khoảng cùng bằng $\dfrac{h}{2}$
Nên $O$ chạy trên đường thẳng $c$ song song và cách đều $a,b$ một khoảng $\dfrac{h}{2}$.
Cho đường tròn (O; R) đường kính AB. Vẽ các tia tiếp tuyến Ax, By với nửa đường tròn. Lấy điểm M di động trên tía Ax, điểm N di động trên tia Oy sao cho \(AM.BN = {R^2}.\)
Chọn câu đúng:
-
A.
MN là tiếp tuyến của đường tròn (O)
-
B.
\(\widehat {MON} = 90^\circ \)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
Đáp án: C
Sử dụng tam giác đồng dạng, tam giác bằng nhau để chứng minh \(OH = R.\)
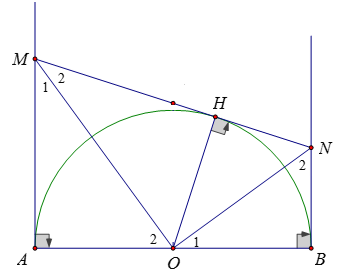
Vẽ \(OH \bot MN,{\rm{ }}H \in MN.\;\) Vì \(AM.BN = {R^2}\; = AO.BO\) nên \(\dfrac{{AM}}{{BO}} = \dfrac{{AO}}{{BN}}\)
Xét ΔAOM và ΔBNO có: \(\widehat {MAO} = \widehat {NBO} = 90^\circ ;\,\dfrac{{AM}}{{BO}} = \dfrac{{AO}}{{BN}}\) \( \Rightarrow \Delta AOM\backsim\Delta BNO{\rm{ }}\left( {c.g.c} \right)\) \( \Rightarrow \widehat {{M_1}} = \widehat {{O_1}};\,\widehat {{O_2}} = \widehat {{N_2}}\)
Do đó góc MON bằng \({90^0}\)
Ta có: \(\dfrac{{AM}}{{BO}} = \dfrac{{OM}}{{ON}} \) (do \(\Delta AOM\backsim\Delta BNO\)) \(\Rightarrow \dfrac{{AM}}{{OM}} = \dfrac{{OA}}{{ON}}\)
Do đó \(\Delta AOM\backsim\Delta ONM{\rm{ }}\left( {c.g.c} \right)\) \( \Rightarrow \widehat {{M_1}} = \widehat {{M_2}}\)
\( ΔAOM = ΔHOM\) (cạnh huyền, góc nhọn)
\( \Rightarrow AO = OH \Rightarrow OH = R,\) do đó MN là tiếp tuyến của đường tròn (O)
Chọn câu đúng.
-
A.
Đường tròn ngoại tiếp tam giác OMN luôn tiếp xúc với đường thẳng AB cố định.
-
B.
Đường tròn ngoại tiếp tam giác OMN luôn tiếp xúc với đường thẳng AM cố định
-
C.
Đường tròn ngoại tiếp tam giác OMN luôn tiếp xúc với đường thẳng BN cố định
-
D.
Cả A, B, C đều sai
Đáp án: A
Gọi K là trung điểm của MN
Sử dụng tính chất tam giác vuông và tính chất đường trung bình của hình thang.
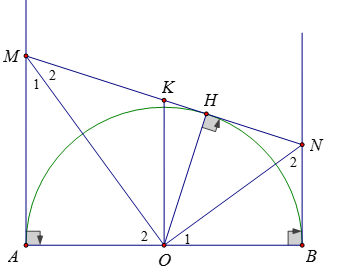
Gọi K là trung điểm của MN
Tam giác MON vuông tại O có OK là trung tuyến \( \Rightarrow KM = KN = KO\)
Suy ra: Đường tròn (K; KO) là đường tròn ngoại tiếp tam giác OMN.
Ta có OK là đường trung bình của hình thang AMNB nên \(OK // AM\)
\( \Rightarrow OK \bot AB\)
Suy ra OK là tiếp tuyến của đường tròn (K). Vậy đường tròn (K) ngoại tiếp tam giác OMN luôn tiếp xúc với một đường thẳng cố định là đường thẳng AB.
Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Trên AO lấy điểm M sao cho \(AM = AB.\) Các tia BM và CM lần lượt cắt đường tròn tại một điểm thứ hai là D và E. Chọn câu đúng.
-
A.
M là tâm đường tròn ngoại tiếp tam giác OBC
-
B.
DE là đường kính của đường tròn (O)
-
C.
M là tâm đường tròn nội tiếp tam giác OBC
-
D.
Cả A, B, C đều sai
Đáp án : B
Sử dụng:
Tâm đường tròn ngoại tiếp tam giác là giao ba đường trung trực
Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác góc trong
Nếu \(AB//d;\,AC//d\) thì \(A,B,C\) thẳng hàng.
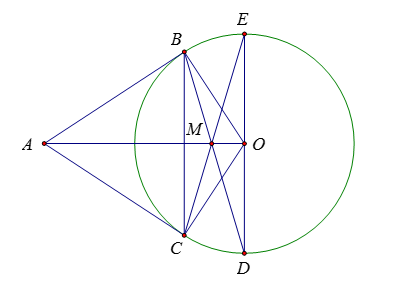
Tam giác ABM có \(AB = AM\) nên ΔABM cân tại A \( \Rightarrow \widehat {ABM} = \widehat {AMB}\,\,\left( 1 \right)\)
Ta có: \(OA ⊥ BC; OB ⊥ AB\) nên: \(\left\{ \begin{array}{l}\widehat {ABM} + \widehat {MBO} = 90^\circ \\\widehat {AMB} + \widehat {MBC} = 90^\circ \end{array} \right.\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \widehat {MBO} = \widehat {MBC}\)
Tương tự \(\widehat {BCM} = \widehat {OCM}\)
Điểm M là giao điểm hai đường phân giác của tam giác OBC nên M là tâm đường tròn nội tiếp tam giác OBC.
Vì tam giác BOD cân tại O \( \Rightarrow \widehat {MBO} = \widehat {MDO}\) mà \(\widehat {MBO} = \widehat {MBC}\) nên \(\widehat {MBC} = \widehat {MDO}\)
Mà hai góc này ở vị trí so le trong nên \(OD // BC\)
Chứng minh tương tự, ta có \(OE // BC\)
\( \Rightarrow D,{\rm{ }}O,{\rm{ }}E\) thẳng hàng
Vậy DE là đường kính của đường tròn (O)
Luyện tập và củng cố kiến thức Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6: Tính chất hai tiếp tuyến cắt nhau Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7,8 Vị trí tương đối của hai đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập hay và khó chương đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 6 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Đường kính và dây của đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Sự xác định của đường tròn- Tính chất đối xứng của đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9










Danh sách bình luận