Bài tập trắc nghiệm Toán lớp 9 có đáp án Bài tập trắc nghiệm Chương 7 Góc với đường tròn

Trắc nghiệm Bài 8: Đường tròn ngoại tiếp, đường tròn nội tiếp Toán 9

Đề bài

Xem đáp án

Làm bài tập

Đề bài

Câu 1 :

Đường tròn ngoại tiếp đa giác là đường tròn

A.

Tiếp xúc với tất cả các cạnh của đa giác đó
B.

Đi qua tất cả các đỉnh của đa giác đó
C.

Cắt tất cả các cạnh của đa giác đó
D.

Đi qua tâm của đa giác đó

Câu 2 :

Số đường tròn nội tiếp của một đa giác đều là

A.

$1$
B.

$2$
C.

$3$
D.

$0$

Câu 3 :

Đường tròn nội tiếp hình vuông cạnh $a$ có bán kính là

A.

$a\sqrt 2 $
B.

$\dfrac{{a\sqrt 2 }}{2}$
C.

$\dfrac{a}{2}$
D.

$\dfrac{{a\sqrt 3 }}{2}$

Câu 4 :

Cho lục giác đều $ABCDEF$ nội tiếp đường tròn tâm $O$ . Tính số đo góc $AOB$ .

A.

$60^\circ $
B.

$120^\circ $
C.

$30^\circ $
D.

$240^\circ $

Câu 5 :

Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính $4\,cm$ (làm tròn đến chữ số thập phân thứ nhất)

A.

$4,702\,cm$
B.

$4,7\,cm$
C.

$4,6\,cm$
D.

$4,72\,cm$

Câu 6 :

Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính $4\,cm$ (làm tròn đến chữ số thập phân thứ nhất).

A.

$5,8\,cm$
B.

$5,81\,cm$
C.

$11,01\,cm$
D.

$11,0\,cm$

Câu 7 :

Tính cạnh của hình vuông nội tiếp $\left( {O;R} \right)$

A.

$\dfrac{R}{{\sqrt 2 }}$
B.

$2R$
C.

$\sqrt 2 R$
D.

$2\sqrt 2 R$

Câu 8 :

Tính độ dài cạnh của tam giác đều nội tiếp $\left( {O;R} \right)$ theo $R.$

A.

$\dfrac{R}{{\sqrt 3 }}$
B.

$\sqrt 3 R$
C.

$R\sqrt 6 $
D.

$3R$

Câu 9 :

Cho $\left( {O;4} \right)$ có dây $AC$ bằng cạnh hình vuông nội tiếp và dây $BC$ bằng cạnh tam giác đều nội tiếp đường tròn đó ( điểm $C$ và $A$ nằm cùng phía với $BO$ ). Tính số đo góc $ACB$

A.

$30^\circ $
B.

$45^\circ $
C.

$60^\circ $
D.

$15^\circ $

Câu 10 :

Cho ngũ giác đều $ABCDE$. Gọi $K$ là giao điểm của $AC$ và $BE$ . Khi đó hệ thức nào dưới đây là đúng?

A.

$C{B^2} = AK.AC$
B.

$O{B^2} = AK.AC$
C.

$AB + BC = AC$
D.

Cả A, B, C đều sai.

Câu 11 :

Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của một hình vuông. Tỉ số $\dfrac{R}{r}$ là:

A.

$\dfrac{1}{{\sqrt 2 }}$
B.

$2$
C.

$\dfrac{{\sqrt 3 }}{2}$
D.

đáp án khác

Câu 12 :

Bát giác đều ABCDEFGH nội tiếp đường tròn bán kính bằng 1. Tính độ dài cạnh AB của bát giác.

A.

$2 - \sqrt 2 $
B.

$2 + \sqrt 2 $
C.

$\sqrt {2 - \sqrt 2 } $
D.

Đáp án khác

Lời giải và đáp án

Câu 1 :

Đường tròn ngoại tiếp đa giác là đường tròn

A.

Tiếp xúc với tất cả các cạnh của đa giác đó
B.

Đi qua tất cả các đỉnh của đa giác đó
C.

Cắt tất cả các cạnh của đa giác đó
D.

Đi qua tâm của đa giác đó

Đáp án : B

Lời giải chi tiết :

Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác .

Câu 2 :

Số đường tròn nội tiếp của một đa giác đều là

A.

$1$
B.

$2$
C.

$3$
D.

$0$

Đáp án : A

Lời giải chi tiết :

Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

Câu 3 :

Đường tròn nội tiếp hình vuông cạnh $a$ có bán kính là

A.

$a\sqrt 2 $
B.

$\dfrac{{a\sqrt 2 }}{2}$
C.

$\dfrac{a}{2}$
D.

$\dfrac{{a\sqrt 3 }}{2}$

Đáp án : C

Phương pháp giải :

+ Sử dụng tính chất của hình vuông

Lời giải chi tiết :

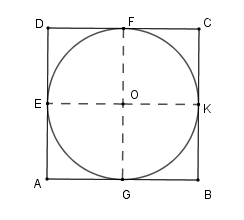
Gọi $O$ là tâm của hình vuông $ABCD$ , $E;\,F;K;\,G$ là trung điểm của $AD,\,DC,\,BC,\,AB$

Khi đó ta có $OE = OF = OK = OG = \dfrac{a}{2}$ . Hay $O$ là tâm đường tròn nội tiếp hình vuông $ABCD$ .

Bán kính đường tròn là $R = \dfrac{a}{2}$ .

Câu 4 :

Cho lục giác đều $ABCDEF$ nội tiếp đường tròn tâm $O$ . Tính số đo góc $AOB$ .

A.

$60^\circ $
B.

$120^\circ $
C.

$30^\circ $
D.

$240^\circ $

Đáp án : A

Phương pháp giải :

+ Sử dụng tính chất lục giác đều

Lời giải chi tiết :

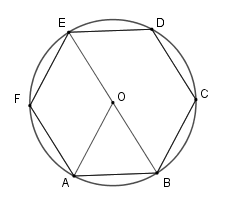
Ta có $AB = BC = CD = DE = EF = FA$ nên số đo cung $AB = \dfrac{1}{6}$ số đo cả đường tròn

Hay $\widehat {AOB} = \dfrac{{360^\circ }}{6} = 60^\circ $ .

Câu 5 :

Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính $4\,cm$ (làm tròn đến chữ số thập phân thứ nhất)

A.

$4,702\,cm$
B.

$4,7\,cm$
C.

$4,6\,cm$
D.

$4,72\,cm$

Đáp án : B

Phương pháp giải :

+ Sử dụng tính mối quan hệ giữa cung và dây cung để tính góc $AOB$

+ Sử dụng hệ thức giữa cạnh và góc trong tam giác.

Lời giải chi tiết :

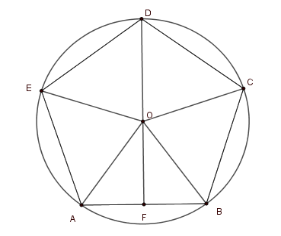
+ Vì $AB = BC = CD = DE = EA$ nên các cung $AB,BC,CD,DE,EA$ bằng nhau

Suy ra $\widehat {AOB} = \dfrac{1}{5}.360^\circ = 72^\circ $

+) Xét tam giác $AOB$ cân tại $O$ có $OF$ là đường cao cũng là đường phân giác nên $\widehat {BOF} = 36^\circ $

Ta có $FB = OB.\sin \widehat {BOF} = 4.\sin 36^\circ \Rightarrow AB = 2FB = 8\sin 36^\circ \approx 4,7\,cm$

Câu 6 :

Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính $4\,cm$ (làm tròn đến chữ số thập phân thứ nhất).

A.

$5,8\,cm$
B.

$5,81\,cm$
C.

$11,01\,cm$
D.

$11,0\,cm$

Đáp án : A

Phương pháp giải :

+ Sử dụng tính chất ngũ giác đều để tính góc $AOB$

+ Sử dụng hệ thức giữa cạnh và góc trong tam giác.

Lời giải chi tiết :

Gọi $O$ là tâm đường tròn nội tiếp ngũ giác đều $ABCDE$, đường cao $OF \bot AB.$

Khi đó bán kính của $\left( O \right)$ là $OF = 4\,cm$ .

Ta có $\widehat {AOB} = \dfrac{{360^\circ }}{5} = 72^\circ $ $ \Rightarrow \widehat {BOF} = 36^\circ $

Xét tam giác $OFB$ có $FB = OF.\tan 36^\circ = 4.\tan 36^\circ \Rightarrow AB = 8.\tan 36^\circ \approx 5,8 \,cm.$

Câu 7 :

Tính cạnh của hình vuông nội tiếp $\left( {O;R} \right)$

A.

$\dfrac{R}{{\sqrt 2 }}$
B.

$2R$
C.

$\sqrt 2 R$
D.

$2\sqrt 2 R$

Đáp án : C

Phương pháp giải :

+ Sử dụng tính chất hình vuông để tìm bán kính đường tròn

+ Sử dụng định lý Pythagore để tìm cạnh của hình vuông

Lời giải chi tiết :

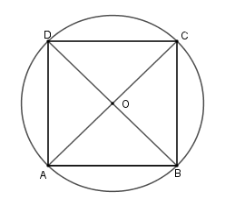
Gọi $ABCD$ là hình vuông cạnh $a$ nội tiếp đường tròn $\left( O \right)$ suy ra $O$ là giao điểm hai đường chéo $AC$ và $BD$

Từ đó $R = OA = \dfrac{{AC}}{2}$ suy ra $AC = 2R$

Áp dụng định lý Pythagore vào tam giác ABC ta có $A{B^2} + B{C^2} = A{C^2} $ suy ra $A{C^2} = {a^2} + {a^2} = 2{a^2}$

Do đó $ AC = a\sqrt 2 = 2R$, suy ra $a = \sqrt 2 R$.

Câu 8 :

Tính độ dài cạnh của tam giác đều nội tiếp $\left( {O;R} \right)$ theo $R.$

A.

$\dfrac{R}{{\sqrt 3 }}$
B.

$\sqrt 3 R$
C.

$R\sqrt 6 $
D.

$3R$

Đáp án : B

Phương pháp giải :

Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng $\frac{\sqrt 3}{3}a$.

Lời giải chi tiết :

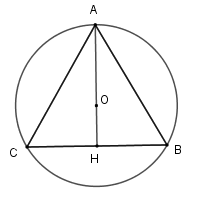
Tam giác đều nội tiếp $\left( {O;R} \right)$ theo $R$ thì đường tròn $\left( {O;R} \right)$ ngoại tiếp tam giác đều.

Đường tròn ngoại tiếp tam giác đều cạnh a có bán kính bằng $\frac{\sqrt 3}{3}a$ hay $R =\frac{\sqrt 3}{3}a$.

Suy ra $a = R:\frac{\sqrt 3}{3} = R.\frac{3}{\sqrt 3} = \sqrt 3R$.

Câu 9 :

A.

$30^\circ $
B.

$45^\circ $
C.

$60^\circ $
D.

$15^\circ $

Đáp án : D

Phương pháp giải :

+ Tìm số đo các cung $BC$ và $AB$ để tìm số đo cung $AC$

+ Sử dụng: số đo góc nội tiếp bằng nửa số đo cung bị chắn

Lời giải chi tiết :

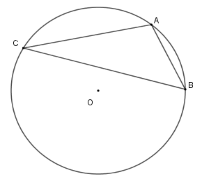
+ Vì $AC$ bằng cạnh của hình vuông nội tiếp $\left( O \right)$ nên số đo cung $AC = 90^\circ $

Vì $BC$ bằng cạnh của tam giác đều nội tiếp $\left( O \right)$ nên số đo cung $BC = 120^\circ $

Từ đó suy ra số đo cung $AB = 120^\circ - 90^\circ = 30^\circ $

+ Vì $\widehat {ACB}$ là góc nội tiếp chắn cung $AB$ nên $\widehat {ACB} = \dfrac{{30^\circ }}{2} = 15^\circ $

Câu 10 :

Cho ngũ giác đều $ABCDE$. Gọi $K$ là giao điểm của $AC$ và $BE$ . Khi đó hệ thức nào dưới đây là đúng?

A.

$C{B^2} = AK.AC$
B.

$O{B^2} = AK.AC$
C.

$AB + BC = AC$
D.

Cả A, B, C đều sai.

Đáp án : A

Phương pháp giải :

Sử dụng tam giác đồng dạng

Lời giải chi tiết :

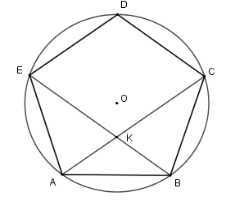
Vì $AB = AE$ (do $ABCDE$ là ngũ giác đều ) nên cung $AB = $ cung $AE$

Xét tam giác $AKB$ và tam giác $ABC$ có

$\widehat A$ chung và $\widehat {KBA} = \widehat {KCB}$ (hai góc nội tiếp chắn hai cung bằng nhau $AB,AE$ )

Suy ra $\Delta AKB\backsim\Delta ABC\left( {g - g} \right)$

$\Rightarrow \dfrac{{AK}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow A{B^2} = AK.AC$ .

Mà $AB = BC$ nên $B{C^2} = AK.AC$ .

Theo bất đẳng thức tam giác thì $AB + BC > AC$ nên C sai

Vì $ABCDE$ là ngũ giác đều nên $BC \ne OB$ nên B sai.

Câu 11 :

Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của một hình vuông. Tỉ số $\dfrac{R}{r}$ là:

A.

$\dfrac{1}{{\sqrt 2 }}$
B.

$2$
C.

$\dfrac{{\sqrt 3 }}{2}$
D.

đáp án khác

Đáp án : D

Phương pháp giải :

Chứng minh bán kính đường tròn ngoại tiếp và nội tiếp hình vuông là cạnh huyền và cạnh góc vuông của một tam giác vuông cân, từ đó suy ra tỉ lệ

Lời giải chi tiết :

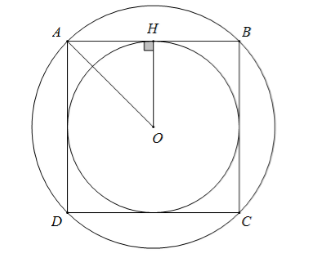
Giả sử hình vuông ABCD nội tiếp đường tròn (O)

Suy ra O cũng là tâm đường tròn nội tiếp hình vuông

Gọi H là trung điểm AB thì $OH \bot AB$ tại H

Ta có R = OA, r = OH

Vì AO là phân giác của góc BAD nên

$\widehat {HAO} = \dfrac{{\widehat {BAD}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ $

Xét tam giác AHO vuông tại H có:

$ \sin \widehat {HAO} = \dfrac{{OH}}{{OA}}$

$ \dfrac{{OH}}{{OA}} = \sin {45^0} = \dfrac{1}{{\sqrt 2 }} $

$\dfrac{{OA}}{{OH}} = \sqrt 2 $ hay $\dfrac{R}{r} = \sqrt 2 .$

Câu 12 :

Bát giác đều ABCDEFGH nội tiếp đường tròn bán kính bằng 1. Tính độ dài cạnh AB của bát giác.

A.

$2 - \sqrt 2 $
B.

$2 + \sqrt 2 $
C.

$\sqrt {2 - \sqrt 2 } $
D.

Đáp án khác

Đáp án : C

Phương pháp giải :

Gọi O là tâm đường tròn ngoại tiếp bát giác đều

Vẽ BH ⊥ AO tại H

Tính BH, OH, AH

Sử dụng hệ thức lượng trong tam giác vuông $AB^2 = AH.AE$ để tính AB

Lời giải chi tiết :

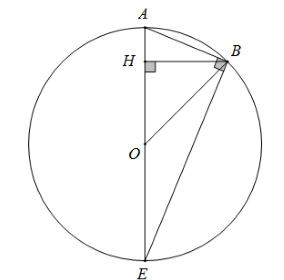
Vì ABCDEFGH là bát giác đều nên góc AOB bằng $\dfrac{{360^\circ }}{8} = 45^\circ $ và AE là đường kính của đường tròn (O) ngoại tiếp bát giác.

Vẽ BH ⊥ AO tại H thì tam giác BHO vuông cân tại H (vì có góc BOH bằng $45^0$.

Theo định lý Pytago ta có $B{H^2} + O{H^2} = O{B^2}$$ \Leftrightarrow 2B{H^2} = O{B^2} $$\Leftrightarrow BH = \dfrac{{OB}}{{\sqrt 2 }}$

Suy ra

$\begin{array}{l}BH = OH = \dfrac{{OB}}{{\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}\\AH = AO - OH = 1 - \dfrac{1}{{\sqrt 2 }}\\AE = 2AO = 2\end{array}$

Vì AE là đường kính của (O) nên ∆ ABE vuông tại B, áp dụng hệ thức lượng trong tam giác vuông ta có

$A{B^2} = AH.AE = \left( {1 - \dfrac{1}{{\sqrt 2 }}} \right).2 = 2 - \sqrt 2 $

$ \Rightarrow AB = \sqrt {2 - \sqrt 2 } $

Trắc nghiệm Bài 9: Độ dài đường tròn, cung tròn Toán 9

Luyện tập và củng cố kiến thức Bài 9: Độ dài đường tròn, cung tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 10: Diện tích hình tròn, quạt tròn Toán 9

Luyện tập và củng cố kiến thức Bài 10: Diện tích hình tròn, quạt tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài tập hay và khó chương góc với đường tròn Toán 9

Luyện tập và củng cố kiến thức Bài tập hay và khó chương góc với đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài tập vận dụng cao từ các đề thi chuyên Toán 9

Luyện tập và củng cố kiến thức Bài tập vận dụng cao từ các đề thi chuyên Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài tập ôn tập chương 7 Toán 9

Luyện tập và củng cố kiến thức Bài tập ôn tập chương 7 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 7: Tứ giác nội tiếp Toán 9

Luyện tập và củng cố kiến thức Bài 7: Tứ giác nội tiếp Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 6: Cung chứa góc Toán 9

Luyện tập và củng cố kiến thức Bài 6: Cung chứa góc Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn Toán 9

Luyện tập và củng cố kiến thức Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 4: Góc tạo bởi tiếp tuyến và dây cung Toán 9

Luyện tập và củng cố kiến thức Bài 4: Góc tạo bởi tiếp tuyến và dây cung Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 3: Góc nội tiếp Toán 9

Luyện tập và củng cố kiến thức Bài 3: Góc nội tiếp Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 2: Liên hệ giữa cung và dây Toán 9

Luyện tập và củng cố kiến thức Bài 2: Liên hệ giữa cung và dây Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 1: Góc ở tâm- Số đo cung Toán 9

Luyện tập và củng cố kiến thức Bài 1: Góc ở tâm- Số đo cung Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết