Trắc nghiệm Bài tập hay và khó chương hệ thức lượng trong tam giác vuông Toán 9
Đề bài
Cho tam giác $ABC$ vuông tại $A$ có $AB = 6cm,{\rm{ }}BC = 10cm,$ đường cao $AH.$ Gọi $E,{\rm{ }}F$ là hình chiếu của $H$ lần lượt lên $AB,{\rm{ }}AC.$
Tính \(EF.\)
-
A.
\(4,8\,cm\)
-
B.
\(2,4\,cm\)
-
C.
\(5,6\,cm\)
-
D.
\(6,4\,cm\)
Chọn câu đúng.
-
A.
$AE.AB = AF.AC.$
-
B.
$AE.AF = AB.AC.$
-
C.
$AE.AC = AF.AB.$
-
D.
$\dfrac{{AE}}{{AB}} = \dfrac{{AF}}{{AC}}.$
Tính: \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
-
A.
\(2\)
-
B.
\( - 1\)
-
C.
\(1\)
-
D.
\(0\)
Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH.$ Qua $B$ vẽ đường thẳng vuông góc với $BC$ cắt đường thẳng $AC$ tại $D.$ Tia phân giác của góc $C$ cắt $AB$ tại $N$ và $BD$ tại $M.$
Chọn câu đúng.
-
A.
\(CN.CB = CM.CD\)
-
B.
\(CN.CM = CD.CB\)
-
C.
\(C{N^2} = CM.CB\)
-
D.
\(CN.CD = CM.CB\)
Chọn câu đúng.
-
A.
\(NA.MD = CA.CD\)
-
B.
\(\dfrac{{NA}}{{CD}} = \dfrac{{CA}}{{MD}}\)
-
C.
\(\dfrac{{NA}}{{MD}} = \dfrac{{CA}}{{CD}}\).
-
D.
Cả A, B, C đều đúng.
Cho tam giác cân \(ABC\) có đáy \(BC = 2a\), cạnh bên bằng \(b\left( {b > a} \right)\).
Tính diện tích tam giác $ABC$
-
A.
\(S = a\sqrt {{b^2} - {a^2}} \)
-
B.
\(S = \dfrac{1}{2}a\sqrt {{b^2} - {a^2}} \)
-
C.
\(S = \dfrac{1}{2}\sqrt {{b^2} - {a^2}} \)
-
D.
\(S = \sqrt {{b^2} - {a^2}} \)
Kẻ \(BK \bot AC\). Tính tỷ số $\dfrac{{AK}}{{AC}}$.
-
A.
$\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{{a^2}}}$
-
B.
$\dfrac{{AK}}{{AC}} = \dfrac{{\left| {2{b^2} - {a^2}} \right|}}{{{b^2}}}$
-
C.
$\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{{b^2}}}$
-
D.
$\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{2b}}$
Cho hình thang \(ABCD\) có \(\widehat A = \widehat D = {90^0},\widehat B = {60^0},CD = 30cm,CA \bot CB\). Tính diện tích của hình thang.
-
A.
\(350\sqrt 3 \,\,c{m^2}\)
-
B.
\(50\sqrt 3 \,\,c{m^2}\)
-
C.
\(250\sqrt 3 \,\,c{m^2}\)
-
D.
\(700\sqrt 3 \,\,c{m^2}\)
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Tính \(\tan B.\tan C\)
-
A.
\(\dfrac{1}{2}\)
-
B.
\(\dfrac{1}{3}\)
-
C.
\(2\)
-
D.
\(3\)
Cho tam giác \(ABC\) vuông tại \(A\),\(AB < AC,\widehat C = \alpha < {45^0}\), đường trung tuyến \(AM\), đường cao \(AH\), \(MA = MB = MC = a.\) Chọn câu đúng.
-
A.
\(\sin 2\alpha = 2\sin \alpha \cos \alpha ;\)
-
B.
\(1 + c{\rm{os}}2\alpha = 2{\cos ^2}\alpha ;\)
-
C.
\(1 - c{\rm{os}}2\alpha = 2si{n^2}\alpha .\)
-
D.
Cả A, B, C đều đúng.
Cho tam giác $ABC$ vuông tại $C,$ đường cao $CK.$ Gọi \(H\) và $I$ theo thứ tự là hình chiếu của K trên $BC$ và $AC.$ Gọi $M$ là chân đường vuông kẻ từ $K$ xuống $IH.$ Chọn câu đúng.
-
A.
\(\dfrac{1}{{K{M^2}}} = \dfrac{1}{{C{H^2}}} + \dfrac{1}{{C{I^2}}}\)
-
B.
\(\dfrac{{AI}}{{BH}} = {\left( {\dfrac{{AC}}{{BC}}} \right)^3}\)
-
C.
A đúng, B sai
-
D.
Cả A, B đều đúng.
Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB,{\rm{ }}AC.$ Chọn câu đúng.
-
A.
$D{E^3} = BD.CE.BC$
-
B.
$D{E^2} = BD.CE.BC$
-
C.
$D{E^4} = BD.CE.BC$
-
D.
Cả A, B, C đều sai.
Tính diện tích một tam giác vuông có chu vi \(72\,cm\), hiệu giữa đường trung tuyến và đường cao ứng với cạnh huyền bằng \(7\,cm.\)
-
A.
\(100\,c{m^2}\)
-
B.
\(44\,c{m^2}\)
-
C.
\(144\,c{m^2}\)
-
D.
\(24\,c{m^2}\)
Cho hình vuông \(ABCD\). Tính \(\cos \,\widehat {MAN}\) biết rằng \(M,N\) theo thứ tự là trung điểm của \(BC;CD.\)
-
A.
\(\dfrac{2}{3}\)
-
B.
\(\dfrac{1}{2}\)
-
C.
\(\dfrac{3}{4}\)
-
D.
\(\dfrac{4}{5}\)
Lời giải và đáp án
Cho tam giác $ABC$ vuông tại $A$ có $AB = 6cm,{\rm{ }}BC = 10cm,$ đường cao $AH.$ Gọi $E,{\rm{ }}F$ là hình chiếu của $H$ lần lượt lên $AB,{\rm{ }}AC.$
Tính \(EF.\)
-
A.
\(4,8\,cm\)
-
B.
\(2,4\,cm\)
-
C.
\(5,6\,cm\)
-
D.
\(6,4\,cm\)
Đáp án: A
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông
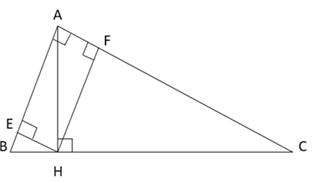
Ta có tam giác $ABC$ vuông tại $A$
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)(cm)
Lại có: $AH$ là đường cao của tam giác vuông $ABC$ nên
\(AH.BC = AB.AC\) (hệ thức lượng trong tam giác vuông)
\( = > AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{6.8}}{{10}} = 4,8\left( {cm} \right)\)
Dễ thấy tứ giác $AFHE$ là hình chữ nhật (có 3 góc vuông)
Nên $EF = AH = 4,8\left( {cm} \right)$
Chọn câu đúng.
-
A.
$AE.AB = AF.AC.$
-
B.
$AE.AF = AB.AC.$
-
C.
$AE.AC = AF.AB.$
-
D.
$\dfrac{{AE}}{{AB}} = \dfrac{{AF}}{{AC}}.$
Đáp án: A
Sử dụng hệ thức lượng trong các tam giác vuông \(AHB;AHC.\)
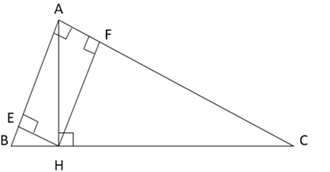
Xét tam giác vuông $AHB$ có đường cao $HE$ , ta có:
\(A{H^2} = AE.AB\)
Tương tự với tam giác vuông $AHC,$ ta có:
\(A{H^2} = AF.AC\)
Do đó: $AE.AB = AF.AC$
Tính: \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
-
A.
\(2\)
-
B.
\( - 1\)
-
C.
\(1\)
-
D.
\(0\)
Đáp án: D
Sử dụng định nghĩa tỉ số lượng giác và định lý Pytago
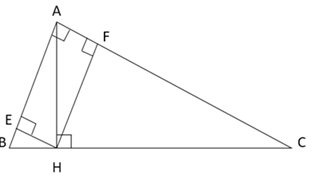
Xét tam giác vuông \(ABC\) có
Ta có: \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}}\)
\(\sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\;\)
\(\tan B = \dfrac{{AC}}{{AB}} \Rightarrow \tan C = \dfrac{{AB}}{{AC}}\)
Vậy \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\;\)
\( = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1\) mà theo Pytago ta có \(A{B^2} + A{C^2} = B{C^2}\) nên
\(A = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0\)
Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH.$ Qua $B$ vẽ đường thẳng vuông góc với $BC$ cắt đường thẳng $AC$ tại $D.$ Tia phân giác của góc $C$ cắt $AB$ tại $N$ và $BD$ tại $M.$
Chọn câu đúng.
-
A.
\(CN.CB = CM.CD\)
-
B.
\(CN.CM = CD.CB\)
-
C.
\(C{N^2} = CM.CB\)
-
D.
\(CN.CD = CM.CB\)
Đáp án: D
Sử dụng tính chất hai tam giác đồng dạng để tìm hệ thức đúng.
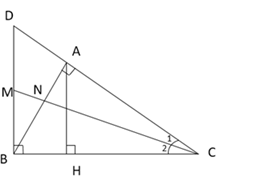
Ta có: \(\widehat {{C_1}} = \widehat {{C_2}}\) (gt)
\( \Rightarrow \Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g)
Suy ra \(\dfrac{{CN}}{{CM}} = \dfrac{{CA}}{{CB}}\,\,\left( 1 \right)\)
Lại có \(\Delta CAB\) đồng dạng với \(\Delta CBD\) (g-g)
Suy ra \(\dfrac{{CA}}{{CB}} = \dfrac{{CB}}{{CD}}\;\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \dfrac{{CN}}{{CM}} = \dfrac{{CB}}{{CD}} \Rightarrow CN.CD = CM.CB\)
Chọn câu đúng.
-
A.
\(NA.MD = CA.CD\)
-
B.
\(\dfrac{{NA}}{{CD}} = \dfrac{{CA}}{{MD}}\)
-
C.
\(\dfrac{{NA}}{{MD}} = \dfrac{{CA}}{{CD}}\).
-
D.
Cả A, B, C đều đúng.
Đáp án: C
Sử dụng tính chất hai tam giác đồng dạng và tính chất đường phân giác để tìm hệ thức đúng.
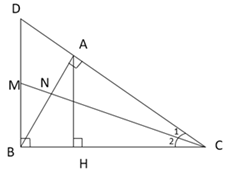
Ta có \(\Delta C{\rm A}{\rm N}\) đồng dạng với $\Delta CBM$ (g-g) (theo câu trước) nên \(\dfrac{{NA}}{{CA}} = \dfrac{{MB}}{{CB}}\;\left( 3 \right)\)
Tia $CM$ là phân giác của góc $BCD$ nên
\(\dfrac{{MB}}{{MD}} = \dfrac{{CB}}{{CD}} \Rightarrow \dfrac{{MB}}{{CB}} = \dfrac{{MD}}{{CD}}\) (4)
Từ (3) và (4) \( \Rightarrow \dfrac{{NA}}{{CA}} = \dfrac{{MD}}{{CD}} \Rightarrow \dfrac{{NA}}{{MD}} = \dfrac{{CA}}{{CD}}\).
Cho tam giác cân \(ABC\) có đáy \(BC = 2a\), cạnh bên bằng \(b\left( {b > a} \right)\).
Tính diện tích tam giác $ABC$
-
A.
\(S = a\sqrt {{b^2} - {a^2}} \)
-
B.
\(S = \dfrac{1}{2}a\sqrt {{b^2} - {a^2}} \)
-
C.
\(S = \dfrac{1}{2}\sqrt {{b^2} - {a^2}} \)
-
D.
\(S = \sqrt {{b^2} - {a^2}} \)
Đáp án: A
Gọi \(H\) là trung điểm của \(BC\).
Tính \(AH\) theo định lý Pytago từ đó tính diện tích tam giác \(ABC.\)
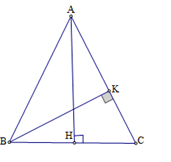
Gọi \(H\) là trung điểm của \(BC\). Theo định lý Pitago ta có:
\(A{H^2} = A{C^2} - H{C^2} = {b^2} - {a^2}\)\( \Rightarrow AH = \sqrt {{b^2} - {a^2}} \)
Suy ra \({S_{ABC}} = \dfrac{1}{2}BC.AH = \dfrac{1}{2}.2a\sqrt {{b^2} - {a^2}}= a\sqrt {{b^2} - {a^2}}\)
Kẻ \(BK \bot AC\). Tính tỷ số $\dfrac{{AK}}{{AC}}$.
-
A.
$\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{{a^2}}}$
-
B.
$\dfrac{{AK}}{{AC}} = \dfrac{{\left| {2{b^2} - {a^2}} \right|}}{{{b^2}}}$
-
C.
$\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{{b^2}}}$
-
D.
$\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{2b}}$
Đáp án: C
Sử dụng diện tích tam giác \(ABC\) đã tính ở câu trước và định lý Pytago để tính \(AK\) , từ đó suy ra tỉ số \(\dfrac{{AK}}{{AC}}.\)
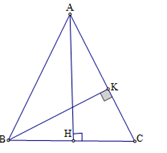
Ta có \(\dfrac{1}{2}BC.AH = \dfrac{1}{2}BK.AC = {S_{ABC}}\)
Suy ra \(BK = \dfrac{{BC.AH}}{{AC}} = \dfrac{{2a}}{b}\sqrt {{b^2} - {a^2}} \).
Áp dụng định lý Pitago trong tam giác vuông \(AKB\) ta có: \(A{K^2} = A{B^2} - B{K^2} = {b^2} - \dfrac{{4{a^2}}}{{{b^2}}}\left( {{b^2} - {a^2}} \right) = \dfrac{{{{\left( {{b^2} - 2{a^2}} \right)}^2}}}{{{b^2}}}\).
Suy ra \(AK = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{b}\) do đó $\dfrac{{AK}}{{AC}} = \dfrac{{\left| {{b^2} - 2{a^2}} \right|}}{{{b^2}}}$.
Cho hình thang \(ABCD\) có \(\widehat A = \widehat D = {90^0},\widehat B = {60^0},CD = 30cm,CA \bot CB\). Tính diện tích của hình thang.
-
A.
\(350\sqrt 3 \,\,c{m^2}\)
-
B.
\(50\sqrt 3 \,\,c{m^2}\)
-
C.
\(250\sqrt 3 \,\,c{m^2}\)
-
D.
\(700\sqrt 3 \,\,c{m^2}\)
Đáp án : A
Kẻ \(CH \bot AB\).
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông
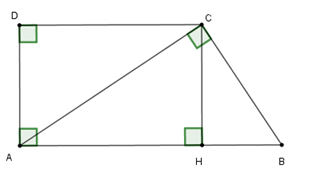
Ta có $\tan \widehat{CAD}=\dfrac{DC}{AD}$
Suy ra $AD = DC : \tan \widehat{CAD} = 30 :\tan 60^0 = 10\sqrt 3$ \(\left( {cm} \right)\).
Kẻ \(CH \bot AB\). Tứ giác \(AHCD\) là hình chữ nhật vì có \(\widehat A = \widehat D = \widehat H = {90^0}\),
suy ra \(AH = CD = 30cm;CH = AD = 10\sqrt 3 \left( {cm} \right)\).
Tam giác \(ACB\) vuông tại \(C\), ta có: \(C{H^2} = HA.HB\),
suy ra \(HB = \dfrac{{C{H^2}}}{{HA}} = \dfrac{{{{\left( {10\sqrt 3 } \right)}^2}}}{{30}} = \dfrac{{300}}{{30}} = 10\left( {cm} \right)\),
do đó \(AB = AH + HB = 30 + 10 = 40\left( {cm} \right).\)
\({S_{ABCD}} = \dfrac{1}{2}CH\left( {AB + CD} \right)=\dfrac{1}{2}.10\sqrt 3 .\left( {40 + 30} \right) = 350\sqrt 3 \left( {c{m^2}} \right).\)
Vậy diện tích hình thang \(ABCD\) bằng \(350\sqrt 3 c{m^2}\)
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Tính \(\tan B.\tan C\)
-
A.
\(\dfrac{1}{2}\)
-
B.
\(\dfrac{1}{3}\)
-
C.
\(2\)
-
D.
\(3\)
Đáp án : D
+ Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
+ Tam giác đồng dạng
+ Tính chất dãy tỉ số bằng nhau
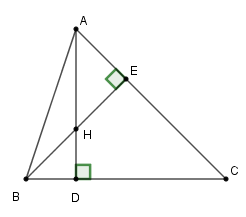
Ta có: \(\tan B = \dfrac{{AD}}{{BD}};\tan C = \dfrac{{AD}}{{CD}}\).
Suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{BD.CD}}\) (1)
\(\widehat {HBD} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)); \(\widehat {HDB} = \widehat {ADC} = {90^0}\).
Do đó \(\Delta BDH \backsim \Delta ADC\) (g.g), suy ra \(\dfrac{{DH}}{{DC}} = \dfrac{{BD}}{{AD}}\), do đó \(BD.DC = DH.AD\) (2).
Từ (1) và (2) suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{DH.AD}} = \dfrac{{AD}}{{DH}}\) (3).
Theo giả thiết \(\dfrac{{HD}}{{AH}} = \dfrac{1}{2}\) suy ra \(\dfrac{{HD}}{{AH + HD}} = \dfrac{1}{{2 + 1}}\) hay \(\dfrac{{HD}}{{AD}} = \dfrac{1}{3}\), suy ra \(AD = 3HD\).
Thay vào (3) ta được: \(\tan B.\tan C = \dfrac{{3HD}}{{DH}} = 3\).
Cho tam giác \(ABC\) vuông tại \(A\),\(AB < AC,\widehat C = \alpha < {45^0}\), đường trung tuyến \(AM\), đường cao \(AH\), \(MA = MB = MC = a.\) Chọn câu đúng.
-
A.
\(\sin 2\alpha = 2\sin \alpha \cos \alpha ;\)
-
B.
\(1 + c{\rm{os}}2\alpha = 2{\cos ^2}\alpha ;\)
-
C.
\(1 - c{\rm{os}}2\alpha = 2si{n^2}\alpha .\)
-
D.
Cả A, B, C đều đúng.
Đáp án : D
Sử dụng định nghĩa tỉ số lượng giác của góc nhọn trong các tam giác thích hợp.
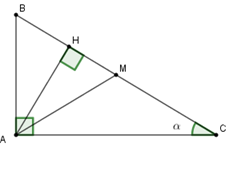
Góc \(2\alpha \) là góc \(AMH\).
+ Ta có \(BC = 2AM;\,AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}\) nên \(\sin 2\alpha = \sin \widehat {AMH} = \dfrac{{AH}}{{AM}} = \dfrac{{2AH}}{{BC}}\)\( = 2.\dfrac{{AB.AC}}{{B{C^2}}} = 2.\dfrac{{AB}}{{BC}}.\dfrac{{AC}}{{BC}}\)
Mà theo định nghĩa tỉ số lượng giác của góc nhọn ta có \(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}}\) nên
\(\sin 2\alpha = 2.\sin \alpha .\cos \alpha \) hay A đúng.
+) Ta có \(\cos 2\alpha = \cos \widehat {AMH} = \dfrac{{HM}}{{AM}}\) (trong tam giác vuông \(AMH\) ) ; \(A{C^2} = HC.BC \Rightarrow HC = \dfrac{{A{C^2}}}{{BC}}\) và \(\cos \alpha = \dfrac{{AC}}{{BC}}\) nên
\(1 + \cos 2\alpha = 1 + \dfrac{{HM}}{{AM}} = \dfrac{{AM + HM}}{{AM}} = \dfrac{{HM + MC}}{{AM}} = \dfrac{{HC}}{{AM}}\) \( = 2\dfrac{{HC}}{{BC}} = 2\dfrac{{A{C^2}}}{{B{C^2}}} = 2{\cos ^2}\alpha ;\)
Do đó B đúng.
+) \(1 - \cos 2\alpha = 1 - \dfrac{{HM}}{{AM}} = \dfrac{{AM - HM}}{{AM}} = \dfrac{{HB}}{{AM}}\)\( = 2\dfrac{{HB}}{{BC}} = 2\dfrac{{A{B^2}}}{{B{C^2}}} = 2{\sin ^2}\alpha \)
Do đó C đúng.
Vậy cả A, B, C đều đúng.
Cho tam giác $ABC$ vuông tại $C,$ đường cao $CK.$ Gọi \(H\) và $I$ theo thứ tự là hình chiếu của K trên $BC$ và $AC.$ Gọi $M$ là chân đường vuông kẻ từ $K$ xuống $IH.$ Chọn câu đúng.
-
A.
\(\dfrac{1}{{K{M^2}}} = \dfrac{1}{{C{H^2}}} + \dfrac{1}{{C{I^2}}}\)
-
B.
\(\dfrac{{AI}}{{BH}} = {\left( {\dfrac{{AC}}{{BC}}} \right)^3}\)
-
C.
A đúng, B sai
-
D.
Cả A, B đều đúng.
Đáp án : D
Chứng minh tứ giác \(HKIC\) là hình chữ nhật
Sử dụng hệ thức lượng trong tam giác vuông thích hợp để biến đổi.
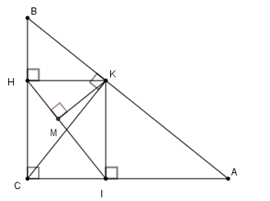
+) Xét tứ giác \(HKIC\) có \(\widehat C = \widehat I = \widehat H = 90^\circ \) nên tứ giác \(HKIC\) là hình chữ nhật suy ra \(HK = CI;HC = IK;KC = HI\) .
+) Xét tam giác vuông \(KHI\) có \(KM\) là chiều cao nên theo hệ thức lượng ta có\(\dfrac{1}{{K{M^2}}} = \dfrac{1}{{K{H^2}}} + \dfrac{1}{{K{I^2}}} = \dfrac{1}{{C{I^2}}} + \dfrac{1}{{H{C^2}}}\) (vì \(HK = CI;HC = IK\)) nên A đúng.
+) Xét tam giác vuông \(KAC\) , theo hệ thức lượng ta có \(K{A^2} = AI.AC \Rightarrow AI = \dfrac{{K{A^2}}}{{AC}}\)
Xét tam giác vuông \(KBC\) , theo hệ thức lượng ta có \(K{B^2} = BH.BC \Rightarrow BH = \dfrac{{K{B^2}}}{{BC}}\)
Lại có theo hệ thức lượng trong tam giác vuông \(ABC\) thì \(A{C^2} = AK.AB \Rightarrow KA = \dfrac{{A{C^2}}}{{AB}}\) ;
\(B{C^2} = KB.AB \Rightarrow KB = \dfrac{{B{C^2}}}{{AB}}\) .
Từ đó ta có \(\dfrac{{AI}}{{BH}} = \dfrac{{K{A^2}}}{{AC}}:\dfrac{{K{B^2}}}{{BC}}\) $ = \left( {\dfrac{{A{C^2}}}{{AB}}:\dfrac{{B{C^2}}}{{AB}}} \right)^2.\dfrac{{BC}}{{AC}}$ \( = {\left( {\dfrac{{AC}}{{BC}}} \right)^4}.\dfrac{{BC}}{{AC}} = {\left( {\dfrac{{AC}}{{BC}}} \right)^3}\)
Do đó B đúng.
Hay cả A, B đều đúng.
Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB,{\rm{ }}AC.$ Chọn câu đúng.
-
A.
$D{E^3} = BD.CE.BC$
-
B.
$D{E^2} = BD.CE.BC$
-
C.
$D{E^4} = BD.CE.BC$
-
D.
Cả A, B, C đều sai.
Đáp án : A
Chứng minh tứ giác \(DHEA\) là hình chữ nhật
Sử dụng hệ thức lượng trong tam giác vuông thích hợp để biến đổi.
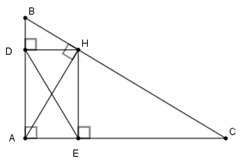
Tứ giác \(DAEH\) có \(\widehat D = \widehat A = \widehat E = 90^\circ \) nên nó là hình chữ nhật suy ra \(AH = DE.\)
Theo hệ thức lượng trong các tam giác vuông \(AHB;\,AHC\) ta có
\(H{B^2} = BD.AB \Rightarrow BD = \dfrac{{H{B^2}}}{{AB}}\) ; \(H{C^2} = CE.CA \Rightarrow CE = \dfrac{{H{C^2}}}{{AC}}\) nên ta có
\(BD.CE.BC = \dfrac{{H{B^2}}}{{AB}}.\dfrac{{H{C^2}}}{{AC}}.BC\)
\( = {\left( {HB.HC} \right)^2}.\dfrac{{BC}}{{AB.AC}}\) mà \(HB.HC = A{H^2}\) (hệ thức lượng trong tam giác vuông \(ABC\) )
\( = A{H^4}.\dfrac{1}{{AH}} = A{H^3} = D{E^3}\) (vì \(AH = DE\) (cmt))
Vậy $D{E^3} = BD.CE.BC$.
Tính diện tích một tam giác vuông có chu vi \(72\,cm\), hiệu giữa đường trung tuyến và đường cao ứng với cạnh huyền bằng \(7\,cm.\)
-
A.
\(100\,c{m^2}\)
-
B.
\(44\,c{m^2}\)
-
C.
\(144\,c{m^2}\)
-
D.
\(24\,c{m^2}\)
Đáp án : C
Đặt \(AM = x\,\left( {x > 0} \right)\) rồi dựa vào hệ thức lượng trong tam giác vuông để tìm ra phương trình ẩn \(x.\)
Giải phương trình ta tìm được \(x.\) Từ đó tính \(AH,BC \Rightarrow {S_{ABC}}.\)
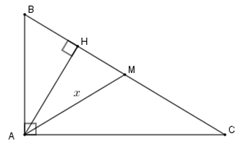
Đặt \(AM = x\,\left( {x > 0;cm} \right) \Rightarrow BC = 2x\,\left( {cm} \right);AH = x - 7\,\left( {cm} \right)\)
Vì chu vi tam giác \(ABC\) là \(72cm\) nên \(AB + AC + BC = 72 \Rightarrow AB + AC = 72 - 2x\,\left( {cm} \right)\)
Theo các hệ thức trong tam giác vuông:
\(A{B^2} + A{C^2} = B{C^2} = 4{x^2}\,\,\left( 1 \right)\) ; \(AB.AC = BC.AH = 2x\left( {x - 7} \right)\,\,\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(A{B^2} + A{C^2} + 2AB.AC = 4{x^2} + 4x\left( {x - 7} \right)\)
\( \Leftrightarrow {\left( {AB + AC} \right)^2} = 8{x^2} - 28x \Leftrightarrow {\left( {72 - 2x} \right)^2} = 8{x^2} - 28x\)
Đưa về phương trình \({x^2} + 65x - 1296 = 0 \Leftrightarrow \left( {x - 16} \right)\left( {x + 81} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\left( N \right)\\x = - 81\,\,\left( L \right)\end{array} \right.\)
Từ đó \(BC = 32\,cm;\,AH = 9\,cm.\) Khi đó \({S_{ABC}} = \dfrac{1}{2}.32.9 = 144\,\,\left( {c{m^2}} \right)\)
Cho hình vuông \(ABCD\). Tính \(\cos \,\widehat {MAN}\) biết rằng \(M,N\) theo thứ tự là trung điểm của \(BC;CD.\)
-
A.
\(\dfrac{2}{3}\)
-
B.
\(\dfrac{1}{2}\)
-
C.
\(\dfrac{3}{4}\)
-
D.
\(\dfrac{4}{5}\)
Đáp án : D
Chứng minh \(AN \bot DM\) . Gọi \(H\) là giao điểm của \(AN\) và \(DM\).
Sử dụng định nghĩa tỉ số lượng giác của góc nhọn để tính \(\cos \,\widehat {MAN}.\)
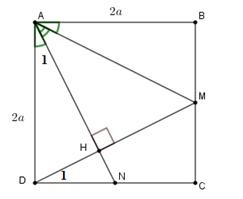
Gọi \(H\) là giao điểm của \(AN\) và \(DM\).
Vì \(ABCD\) là hình vuông và \(M,N\) theo thứ tự là trung điểm của \(BC;CD.\)
Nên \(AD = DC;\,DN = CM\)
Từ đó $\Delta ADN = \Delta DCM\,\left( {c.g.c} \right)$ nên \(\widehat {{A_1}} = \widehat {{D_1}} \Rightarrow AH \bot DM\) (do $\widehat {{A_1}} + \widehat {AND} = 90^\circ \Rightarrow \widehat {{D_1}} + \widehat {HND} = 90^\circ \Rightarrow \widehat {DHN} = 90^\circ $ )
Suy ra \(\cos \widehat {MAN} = \dfrac{{AH}}{{AM}}\)
Đặt \(AB = AD = 2a\) ta tính được \(AM = AN = a\sqrt 5 \)
Từ \(A{D^2} = AH.AN\) ta có \(AH = \dfrac{{4a}}{{\sqrt 5 }}\) . Do đó
\(\cos \widehat {MAN} = \dfrac{{AH}}{{AM}} = \dfrac{{4a}}{{\sqrt 5 }}:\left( {a\sqrt 5 } \right) = \dfrac{4}{5}.\)
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 5 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Ứng dụng thực tế tỉ số lượng giác của góc nhọn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Tỉ số lượng giác của góc nhọn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9










Danh sách bình luận