Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
Đề bài
Cho hình nón có bán kính đáy \(R = 3\,\left( {cm} \right)\) và chiều cao \(h = 4\,\left( {cm} \right)\) . Diện tích xung quanh của hình nón là
-
A.
\(25\pi \) \(\left( {c{m^2}} \right)\)
-
B.
\(12\pi \) \(\left( {c{m^2}} \right)\)
-
C.
\(20\pi \) \(\left( {c{m^2}} \right)\)
-
D.
\(15\pi \) \(\left( {c{m^2}} \right)\)
Cho hình nón có đường kính đáy \(d = 10\,cm\) và diện tích xung quanh \(65\pi \,\left( {c{m^2}} \right)\). Tính thể tích khối nón.
-
A.
\(100\pi \,\left( {c{m^3}} \right)\)
-
B.
\(120\pi \,\left( {c{m^3}} \right)\)
-
C.
\(300\pi \,\left( {c{m^3}} \right)\)
-
D.
\(200\pi \,\left( {c{m^3}} \right)\)
Cho hình nón có chiều cao \(h = 10\,cm\) và thể tích \(V = 1000\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón
-
A.
\(100\pi \,\left( {c{m^2}} \right)\)
-
B.
\((300+200\sqrt3)\pi \,\left( {c{m^2}} \right)\)
-
C.
\(300\pi \,\left( {c{m^2}} \right)\)
-
D.
\(250\pi \,\left( {c{m^2}} \right)\)
Một chiếc xô hình nón cụt làm bằng tôn để đựng nước. Các bán kính đáy là $10\,cm$ và $5cm$, chiều cao là $20cm$ . Tính dung tích của xô.
-
A.
\(\dfrac{{3500\pi }}{3}\,\,\left( {c{m^3}} \right)\)
-
B.
\(3500\pi \,\left( {c{m^3}} \right)\)
-
C.
\(\dfrac{{350\pi }}{3}\,\left( {c{m^3}} \right)\)
-
D.
\(350\pi \,\left( {c{m^3}} \right)\)
Cho tam giác vuông \(ABC\) vuông tại \(A\) có \(BC = 20\,cm;AC = 12\,cm\) . Quay tam giác \(ABC\) cạnh \(AB\) ta được một hình nón có thể tích là :
-
A.
\(2304\,\,\left( {c{m^3}} \right)\)
-
B.
\(1024\pi \,\,\left( {c{m^3}} \right)\)
-
C.
\(786\pi \,\,\left( {c{m^3}} \right)\)
-
D.
\(768\pi \,\,\left( {c{m^3}} \right)\)
Cho hình thang vuông $ABDC$ vuông tại $A$ và $B$ , biết cạnh $AB = BC = 3m,AD = 5cm$. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh $AB$ .
-
A.
$7\pi \,\,\left( {c{m^2}} \right)$
-
B.
$7\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
-
C.
$7\sqrt {10} \,\,\left( {c{m^2}} \right)$
-
D.
$\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh của hình nón đó
-
A.
Tăng \(4\) lần
-
B.
Giảm \(4\) lần
-
C.
Tăng \(2\) lần
-
D.
Không đổi
Cho tam giác \(ABC\) đều cạnh \(a\) , đường trung tuyến \(AM\) . Quay tam giác \(ABC\) quanh cạnh \(AM\) . Tính diện tích toàn phần của hình nón tạo thành.
-
A.
\(\dfrac{{3\pi {a^2}}}{2}\)
-
B.
\(\dfrac{{3\pi {a^2}}}{4}\)
-
C.
\(\dfrac{{5\pi {a^2}}}{2}\)
-
D.
\(\dfrac{{\pi {a^2}}}{2}\)
Cho một hình quạt tròn có bán kính \(20\,cm\) và góc ở tâm là ${144^o}$ . Người ta uốn hình quạt này thành một hình nón. Tính thể tích của khối nón đó.
-
A.
\(256\pi \sqrt {21} \,\left( {c{m^3}} \right)\)
-
B.
\(\dfrac{{24\pi \sqrt {21} }}{3}\,\left( {c{m^3}} \right)\)
-
C.
\(\dfrac{{256\pi }}{3}\,\left( {c{m^3}} \right)\)
-
D.
\(\dfrac{{256\pi \sqrt {21} }}{3}\,\left( {c{m^3}} \right)\)
Từ một khúc gỗ hình trụ cao $15\,cm$, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là $640\pi \,\,c{m^3}$ .
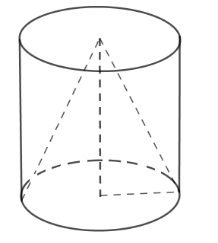
Tính thể tích của khúc gỗ hình trụ.
-
A.
\(960\pi \,\left( {c{m^3}} \right)\)
-
B.
\(320\pi \,\left( {c{m^3}} \right)\)
-
C.
\(640\pi \,\left( {c{m^3}} \right)\)
-
D.
\(690\pi \,\left( {c{m^3}} \right)\)
Tính diện tích xung quanh của hình nón.
-
A.
\(136\pi \,\left( {c{m^2}} \right)\)
-
B.
\(120\pi \,\left( {c{m^2}} \right)\)
-
C.
\(272\pi \,\left( {c{m^2}} \right)\)
-
D.
\(163\pi \,\left( {c{m^2}} \right)\)
Lời giải và đáp án
Cho hình nón có bán kính đáy \(R = 3\,\left( {cm} \right)\) và chiều cao \(h = 4\,\left( {cm} \right)\) . Diện tích xung quanh của hình nón là
-
A.
\(25\pi \) \(\left( {c{m^2}} \right)\)
-
B.
\(12\pi \) \(\left( {c{m^2}} \right)\)
-
C.
\(20\pi \) \(\left( {c{m^2}} \right)\)
-
D.
\(15\pi \) \(\left( {c{m^2}} \right)\)
Đáp án : D
Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\) để tính đường sinh
Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\)
Vì \({R^2} + {h^2} = {l^2}\) hay \({3^2} + {4^2} = {l^2}\)
nên \({l^2} = 25\) suy ra \(l = 5\,cm\)
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = \pi Rl = \pi .3.5 = 15\pi \,\,\left( {c{m^2}} \right)\)
Cho hình nón có đường kính đáy \(d = 10\,cm\) và diện tích xung quanh \(65\pi \,\left( {c{m^2}} \right)\). Tính thể tích khối nón.
-
A.
\(100\pi \,\left( {c{m^3}} \right)\)
-
B.
\(120\pi \,\left( {c{m^3}} \right)\)
-
C.
\(300\pi \,\left( {c{m^3}} \right)\)
-
D.
\(200\pi \,\left( {c{m^3}} \right)\)
Đáp án : A
Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\) để tính đường sinh.
Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\) để tìm chiều cao hình nón
Sử dụng công thức thể tich khối nón \(V = \dfrac{1}{3}\pi {R^2}h.\)
Bán kính đường tròn đáy là:
\(R = \dfrac{d}{2} = \dfrac{{10}}{2} = 5\,cm\)
Diện tích xung quanh là:
\({S_{xq}} = \pi Rl = \pi .5.l = 65\pi \)
Suy ra \(l = 13\,cm\)
Ta có \({R^2} + {h^2} = {l^2}\)
\({5^2} + {h^2} = {13^2}\)
\({h^2} = 144\)
Suy ra \( h = 12\,cm\)
Thể tích khối nón là:
\(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.5^2}.12 \)
\(= 100\pi \,\left( {c{m^3}} \right)\)
Cho hình nón có chiều cao \(h = 10\,cm\) và thể tích \(V = 1000\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón
-
A.
\(100\pi \,\left( {c{m^2}} \right)\)
-
B.
\((300+200\sqrt3)\pi \,\left( {c{m^2}} \right)\)
-
C.
\(300\pi \,\left( {c{m^2}} \right)\)
-
D.
\(250\pi \,\left( {c{m^2}} \right)\)
Đáp án : B
Sử dụng công thức thể tich khối nón \(V = \dfrac{1}{3}\pi {R^2}h\) để tính bán kính đường tròn đáy
Sử dụng công thức liên hệ\({R^2} + {h^2} = {l^2}\) để tìm đường sinh của hình nón
Sử dụng công thức tính diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\)
Ta có \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {R^2}.10 = 1000\pi \)
nên \({R^2} = 300\) suy ra \( R = 10\sqrt 3 \)
Và \({R^2} + {h^2} = {l^2}\) hay \( {10^2} + {\left( {10\sqrt 3 } \right)^2} = {l^2} \) suy ra \( l = 20\,cm\)
Diện tích toàn phần của hình nón là:
\({S_{tp}} = \pi Rl + \pi {R^2} = \pi .10\sqrt3.20 + \pi.300= (300+200\sqrt3)\pi \,\left( {c{m^2}} \right)\)
Một chiếc xô hình nón cụt làm bằng tôn để đựng nước. Các bán kính đáy là $10\,cm$ và $5cm$, chiều cao là $20cm$ . Tính dung tích của xô.
-
A.
\(\dfrac{{3500\pi }}{3}\,\,\left( {c{m^3}} \right)\)
-
B.
\(3500\pi \,\left( {c{m^3}} \right)\)
-
C.
\(\dfrac{{350\pi }}{3}\,\left( {c{m^3}} \right)\)
-
D.
\(350\pi \,\left( {c{m^3}} \right)\)
Đáp án : A
Sử dụng công thức tính thể tích khối nón cụt $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}).$
Ta có $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}) = \dfrac{1}{3}\pi .20.\left( {{{10}^2} + 10.5 + {5^2}} \right) = \dfrac{{3500\pi }}{3}\,\,\left( {c{m^3}} \right)$
Cho tam giác vuông \(ABC\) vuông tại \(A\) có \(BC = 20\,cm;AC = 12\,cm\) . Quay tam giác \(ABC\) cạnh \(AB\) ta được một hình nón có thể tích là :
-
A.
\(2304\,\,\left( {c{m^3}} \right)\)
-
B.
\(1024\pi \,\,\left( {c{m^3}} \right)\)
-
C.
\(786\pi \,\,\left( {c{m^3}} \right)\)
-
D.
\(768\pi \,\,\left( {c{m^3}} \right)\)
Đáp án : D
Sử dụng công thức tính thể tích khối nón $V = \dfrac{1}{3}\pi {R^2}h$
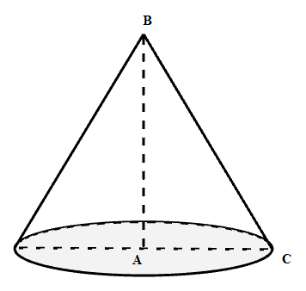
Khi quay tam giác \(ABC\) quanh cạnh \(AB\) ta được một hình nón có chiều cao \(AB\) và bán kính đường tròn đáy là cạnh \(AC\) .
Theo định lí Pytagore ta có:
\(A{B^2} = B{C^2} - A{C^2} = {20^2} - {12^2} = 256\) suy ra \(AB = 16\)
Thể tích của khối nón là:
\(V = \dfrac{1}{3}\pi A{C^2}AB = \dfrac{1}{3}\pi {.12^2}.16 = 768\pi \,\,\left( {c{m^3}} \right)\)
Cho hình thang vuông $ABDC$ vuông tại $A$ và $B$ , biết cạnh $AB = BC = 3m,AD = 5cm$. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh $AB$ .
-
A.
$7\pi \,\,\left( {c{m^2}} \right)$
-
B.
$7\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
-
C.
$7\sqrt {10} \,\,\left( {c{m^2}} \right)$
-
D.
$\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
Đáp án : B
Tính đáy \(BD\)và \(CD\) theo định lý Pytago
Sử dụng công thức diện tích xung quanh hình nón cụt ${S_{xq}} = \pi (R + r)l.$
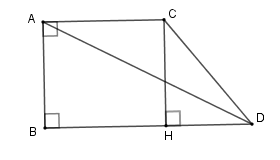
Xét tam giác vuông \(ABD\) ta có \(BD = \sqrt {A{D^2} - A{B^2}} = \sqrt {{5^2} - {3^2}} = 4\,\,\left( {cm} \right)\)
Kẻ $CH \bot BD$ tại \(H\) . Khi đó \(ACHB\) là hình vuông nên\(CH = AB = AC = BH = 3\,cm \Rightarrow HD = 4 - 3 = 1\,cm\)
Xét tam giác vuông \(CHD\) ta có \(C{D^2} = C{H^2} + H{D^2} = {3^2} + {1^2}=10\Rightarrow CD = \sqrt {10} \)
Khi quay hình thang vuông \(ABDC\) quanh cạnh \(AB\) ta được hình nón cụt có bán kính đáy nhỏ \(AC\) , bán kính đáy lớn \(BD\) , đường sinh \(CD\) và chiều cao \(AB\) .
Khi đó diện tích xung quanh hình nón cụt là ${S_{xq}} = \pi (R + r)l = \pi \left( {3 + 4} \right)\sqrt {10} = 7\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh của hình nón đó
-
A.
Tăng \(4\) lần
-
B.
Giảm \(4\) lần
-
C.
Tăng \(2\) lần
-
D.
Không đổi
Đáp án : A
Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\)
Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\) .
Ta có đường sinh mới là: \({l'^2} = {\left( {2R} \right)^2} + {\left( {2h} \right)^2} = 4\left( {{R^2} + {h^2}} \right) = {\left( {2l} \right)^2} \)
Suy ra \(l' = 2l\)
Khi đó diện tích xung quanh mới là:
\({S'_{xq}} = \pi .\left( {2R} \right).\left( {2l} \right) = 4.\pi Rl = 4{S_{xq}}\) .
Vậy diện tích xung quanh của hình nón tăng \(4\) lần.
Cho tam giác \(ABC\) đều cạnh \(a\) , đường trung tuyến \(AM\) . Quay tam giác \(ABC\) quanh cạnh \(AM\) . Tính diện tích toàn phần của hình nón tạo thành.
-
A.
\(\dfrac{{3\pi {a^2}}}{2}\)
-
B.
\(\dfrac{{3\pi {a^2}}}{4}\)
-
C.
\(\dfrac{{5\pi {a^2}}}{2}\)
-
D.
\(\dfrac{{\pi {a^2}}}{2}\)
Đáp án : B
Sử dụng công thức tính diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\) .
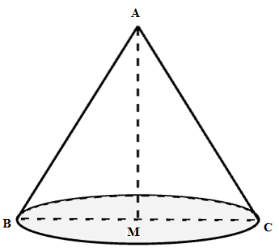
Xét tam giác \(ABC\) đều có \(AM\) vừa là đường trung tuyến, đường cao, đường phân giác.
Nên ta có \(MC = \dfrac{{BC}}{2} = \dfrac{a}{2}\) .
Khi quay tam giác $ABC$ quanh cạnh \(AM\) ta được hình nón đỉnh \(A\) , bán kính đáy là \(MC\) , đường sinh \(AC\) và chiều cao \(AM\) .
Diện tích toàn phần của hình nón là \({S_{tp}} = \pi Rl + \pi {R^2} = \pi .MC.AC + \pi .M{C^2} = \pi .\dfrac{a}{2}.a + \pi .{\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3\pi {a^2}}}{4}\) .
Cho một hình quạt tròn có bán kính \(20\,cm\) và góc ở tâm là ${144^o}$ . Người ta uốn hình quạt này thành một hình nón. Tính thể tích của khối nón đó.
-
A.
\(256\pi \sqrt {21} \,\left( {c{m^3}} \right)\)
-
B.
\(\dfrac{{24\pi \sqrt {21} }}{3}\,\left( {c{m^3}} \right)\)
-
C.
\(\dfrac{{256\pi }}{3}\,\left( {c{m^3}} \right)\)
-
D.
\(\dfrac{{256\pi \sqrt {21} }}{3}\,\left( {c{m^3}} \right)\)
Đáp án : D
Sử dụng công thức thể tích khối nón $V = \dfrac{1}{3}\pi {R^2}h$
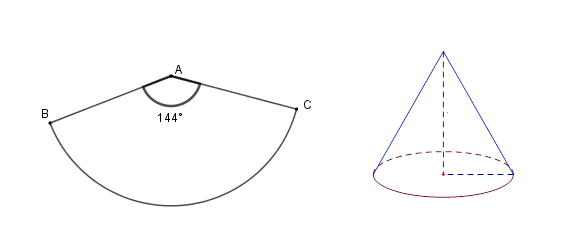
Ta uốn hình quạt \(BAC\) thành hình nón đỉnh \(A\) , đường sinh \(AB = 20\,cm\) .
Khi đó độ dài cung \(BC\) chính là chu vi đáy của hình nón
Ta có độ dài cung \(BC\) là \({l_{BC}} = \dfrac{{\pi .20.144}}{{180}} = 16\pi \)
Khi đó chu vi đáy của hình nón là:
\(C = 2\pi R = 16\pi\) suy ra \( R = 8\,cm\)
Suy ra \({h^2} = {l^2} - {R^2} = {20^2} - {8^2} \) suy ra \( h = 4\sqrt {21} \,cm\)
Thể tích khối nón là:
\(V = \dfrac{1}{3}\pi {.8^2}.4\sqrt {21} = \dfrac{{256\pi \sqrt {21} }}{3}\) \(\left( {c{m^3}} \right)\)
Từ một khúc gỗ hình trụ cao $15\,cm$, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là $640\pi \,\,c{m^3}$ .

Tính thể tích của khúc gỗ hình trụ.
-
A.
\(960\pi \,\left( {c{m^3}} \right)\)
-
B.
\(320\pi \,\left( {c{m^3}} \right)\)
-
C.
\(640\pi \,\left( {c{m^3}} \right)\)
-
D.
\(690\pi \,\left( {c{m^3}} \right)\)
Đáp án: A
Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\) và thể tích khối nón \(V = \dfrac{1}{3}{R^2}h\) để suy ra mối quan hệ giữa thể tích hai khối và phần gỗ bỏ đi.
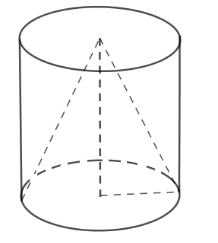
Ta thấy hình nón có bán kính đáy bằng bán kính đáy hình trụ và chiều cao bằng chiều cao hình trụ nên
\({V_{trụ}} = \pi {R^2}h\) và \({V_{nón}} = \dfrac{1}{3}\pi {R^2}h\)
Suy ra \({V_{trụ}} = 3{V_{nón}}\).
Do đó phần gỗ bỏ đi chiếm \(\dfrac{2}{3}\) thể tích khối trụ.
Nên thể tích khối trụ là \({V_{trụ}} = 640\pi :\dfrac{2}{3} = 960\pi \,\,\left( {c{m^3}} \right)\) .
Tính diện tích xung quanh của hình nón.
-
A.
\(136\pi \,\left( {c{m^2}} \right)\)
-
B.
\(120\pi \,\left( {c{m^2}} \right)\)
-
C.
\(272\pi \,\left( {c{m^2}} \right)\)
-
D.
\(163\pi \,\left( {c{m^2}} \right)\)
Đáp án: A
Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\) để tìm bán kính đáy
Sử dụng công thức tính diện tích xung quanh hình nón \(S = \pi Rl\).
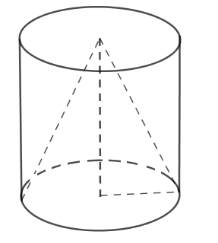
Ta có \({V_{trụ}} = \pi {R^2}h = 960\pi \)
\(\pi {R^2}.15 = 960\pi \)
Suy ra \( R = 8\,cm\) nên bán kính đáy của hình nón là \(R = 8\,cm\).
Chiều cao hình nón \(h = 15\,cm\) suy ra đường sinh hình nón \({l^2} = {h^2} + {R^2} \) suy ra \(l = 17\,cm\)
Diện tích xung quanh hình nón là:
\(S = \pi Rl = \pi .8.17 = 136\pi \,\left( {c{m^2}} \right)\) .
Luyện tập và củng cố kiến thức Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 8 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9










Danh sách bình luận