-
Khảo sát chất lượng đầu năm
-
Chương 1 Căn bậc hai - Căn bậc ba
-
Chương 2 Hàm số bậc nhất
-
Chương 3 Hệ hai phương trình bậc nhất hai ẩn
- Bài 1: Phương trình bậc nhất hai ẩn
- Bài 2: Hệ hai phương trình bậc nhất hai ẩn
- Bài 3: Giải hệ phương trình bằng phương pháp thế
- Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
- Hệ phương trình bậc nhất hai ẩn chứa tham số
- Bài 5,6: Giải bài toán bằng cách lập hệ phương trình
- Bài tập hay và khó chương 3 về hệ phương trình
- Bài tập ôn tập chương 3
-
Chương 4 Hàm số y=ax^2. Phương trình bậc hai một ẩn
- Bài 1,2: Hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2
- Bài 3,4: Phương trình bậc hai một ẩn và công thức nghiệm
- Bài 5: Công thức nghiệm thu gọn
- Bài 6: Hệ thức Vi-ét và ứng dụng
- Bài 7: Phương trình quy về phương trình bậc hai
- Sự tương giao giữa đường thẳng và Parabol
- Bài 8: Giải bài toán bằng cách lập phương trình
- Hệ phương trình đối xứng
- Bài tập hay và khó chương 4: Sự tương giao của đường thẳng và parabol
- Tổng hợp câu hay và khó về giải bài toán bằng cách lập phương trình, hệ phương trình
- Tổng hợp câu hay và khó về hệ thức Vi-et
- Bài tập ôn tập chương 4
-
Chương 5 Hệ thức lượng trong tam giác vuông
-
Chương 6 Đường tròn
- Sự xác định của đường tròn- Tính chất đối xứng của đường tròn
- Bài 2: Đường kính và dây của đường tròn
- Bài 4: Vị trí tương đối giữa đường thẳng và đường tròn
- Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6: Tính chất hai tiếp tuyến cắt nhau
- Bài 7,8: Vị trí tương đối của hai đường tròn
- Bài tập hay và khó chương đường tròn
- Bài tập ôn tập chương 6
-
Chương 7 Góc với đường tròn
- Bài 1: Góc ở tâm- Số đo cung
- Bài 2: Liên hệ giữa cung và dây
- Bài 3: Góc nội tiếp
- Bài 4: Góc tạo bởi tiếp tuyến và dây cung
- Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn
- Bài 6: Cung chứa góc
- Bài 7: Tứ giác nội tiếp
- Bài 8: Đường tròn ngoại tiếp, đường tròn nội tiếp
- Bài 9: Độ dài đường tròn, cung tròn
- Bài 10: Diện tích hình tròn, quạt tròn
- Bài tập hay và khó chương góc với đường tròn
- Bài tập vận dụng cao từ các đề thi chuyên
- Bài tập ôn tập chương 7
-
Chương 8 Hình trụ - hình nón - hình cầu
Trắc nghiệm Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông Toán 9
Đề bài
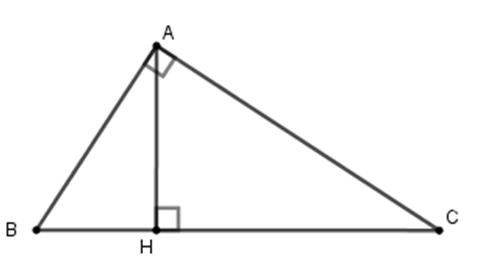
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng?
-
A.
$A{H^2} = AB.AC$
-
B.
$A{H^2} = BH.CH$
-
C.
$A{H^2} = AB.BH$
-
D.
$A{H^2} = CH.BC$
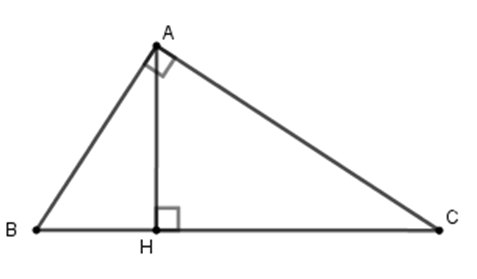
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là sai?
-
A.
$A{B^2} = BH.BC$
-
B.
$A{C^2} = CH.BC$
-
C.
$AB.AC = AH.BC$
-
D.
$A{H^2} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}}$
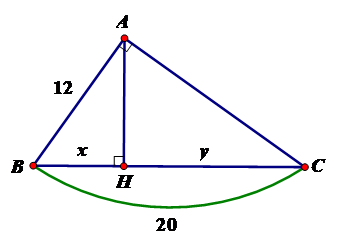
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = 7,2;y = 11,8$
-
B.
$x = 7;y = 12$
-
C.
$x = 7,2;y = 12,8$
-
D.
$x = 7,2;y = 12$
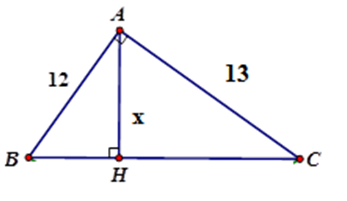
Tính $x$ trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai)
-
A.
$x \approx 8,81$
-
B.
$x \approx 8,82$
-
C.
$x \approx 8,83$
-
D.
$x \approx 8,80$
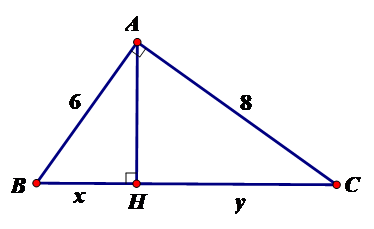
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = 3,6;y = 6,4$
-
B.
$y = 3,6;x = 6,4$
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
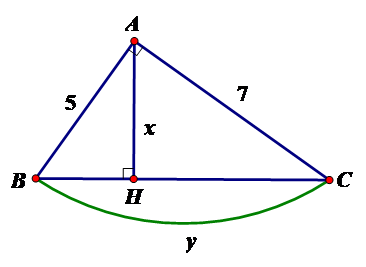
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
-
B.
$y = \dfrac{{35\sqrt {74} }}{{74}};x= \sqrt {74} $
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Cho tam giác $ABC$ vuông tại $A$, $AH \bot BC$( $H$ thuộc $BC$ ). Cho biết $AB:AC = 3:4$ và $BC = 15cm.$ Tính độ dài đoạn thẳng $BH$.
-
A.
$BH = 5,4$
-
B.
$BH = 4,4$
-
C.
$BH = 5,2$
-
D.
$BH = 5$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH.$ Cho biết $AB:AC = 3:4$ và $AH = 6cm.$ Tính độ dài các đoạn thẳng $CH.$
-
A.
$CH = 8$
-
B.
$CH = 6$
-
C.
$CH = 10$
-
D.
$CH = 12$
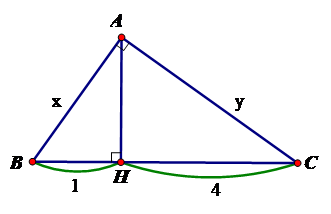
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = 2\sqrt 5 ;y = \sqrt 5 $
-
B.
$x = \sqrt 5 ;y = 3\sqrt 5 $
-
C.
$x = \sqrt 5 ;y = 2\sqrt 5 $
-
D.
$x = 2\sqrt 5 ;y = 2\sqrt 5 $
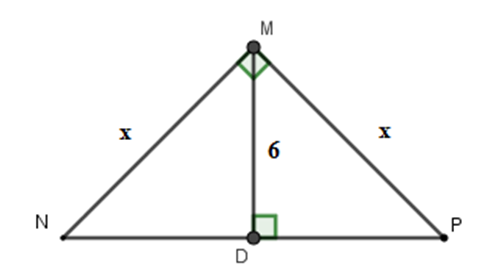
Tính $x$ trong hình vẽ sau:
-
A.
$x = 6\sqrt 2 $
-
B.
$x = 6$
-
C.
$x = 6\sqrt 3 $
-
D.
$x = \sqrt {82} $
Cho ABCD là hình thang vuông tại $A$ và $D.$Đường chéo $BD$ vuông góc với $BC.$ Biết $AD = 12cm,DC = 25cm$ . Tính độ dài $BC$, biết $BC < 20$
-
A.
$BC = 15\,cm$
-
B.
$BC = 16\,cm$
-
C.
$BC = 14\,cm$
-
D.
$BC = 17\,cm$
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB:AC = 3:4\) và \(AB + AC = 21cm\).
Tính các cạnh của tam giác \(ABC\).
-
A.
$AB = 9;AC = 10;BC = 15$
-
B.
$AB = 9;AC = 12;BC = 15$
-
C.
$AB = 8;AC = 10;BC = 15$
-
D.
$AB = 8;AC = 12;BC = 15$
Tính độ dài các đoạn \(AH,BH,CH\).
-
A.
$BH = 7,2;AH = 5,4;CH = 9,6$
-
B.
$CH = 7,2;BH = 5,4;AH = 9,6$
-
C.
$AH = 7,2;BH = 5,4;CH = 9$
-
D.
$AH = 7,2;BH = 5,4;CH = 9,6$
Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB, AC.$(hình vẽ)
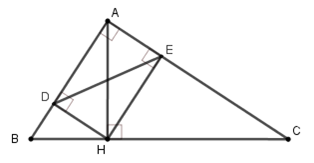
Tỉ số $\dfrac{{A{B^2}}}{{A{C^2}}}$ bằng với tỉ số nào sau đây?
-
A.
$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HC}}{{HB}}$
-
B.
$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HB}}{{HC}}$
-
C.
$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HA}}{{HB}}$
-
D.
$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HC}}{{HA}}$
Tỉ số $\dfrac{{A{B^3}}}{{A{C^3}}}$ bằng với tỉ số nào sau đây?
-
A.
$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{BD}}{{EC}}$
-
B.
$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{AD}}{{EC}}$
-
C.
$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{BD}}{{ED}}$
-
D.
$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{EC}}{{BD}}$
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Cho biết $BH = 4cm,CH = 9cm$. Gọi $D,E$ lần lượt là hình chiếu vuông góc của $H$ trên các cạnh $AB$ và $AC$. Các đường thẳng vuông góc với $DE$ tại $D$ và $E$ lần lượt cắt $BC$ tại $M,N$ . (hình vẽ)
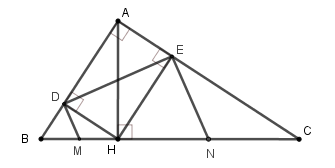
Tính độ dài đoạn thẳng $DE$.
-
A.
$DE = 5\,cm$
-
B.
$DE = 8\,cm$
-
C.
$DE = 7\,cm$
-
D.
$DE = 6\,cm$
Kết luận nào sau đây là đúng?
-
A.
\(MN = \dfrac{1}{3}BC\)
-
B.
\(MN = \dfrac{1}{2}BC\)
-
C.
\(MN = \dfrac{3}{4}BC\)
-
D.
\(MN = \dfrac{2}{3}BC\)
Tính diện tích tứ giác $DENM$
-
A.
\({S_{DENM}} = 19,5\,c{m^2}\)
-
B.
\({S_{DENM}} = 20,5\,c{m^2}\)
-
C.
\({S_{DENM}} = 19\,c{m^2}\)
-
D.
\({S_{DENM}} = 21,5\,c{m^2}\)
Cho tam giác $CDE$ nhọn, đường cao $CH.$ Gọi $M,N$ theo thứ tự là hình chiếu của $H$ lên $CD,CE.$ (hình vẽ)
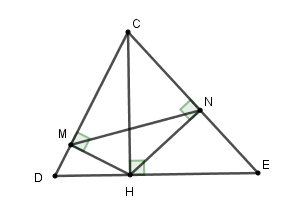
Tích $CD.CM$ bằng
-
A.
\(CH.CE\)
-
B.
\(CE.CN\)
-
C.
\(CH.CN\)
-
D.
\(CD.CN\)
Tam giác $CMN$ đồng dạng với tam giác nào dưới đây?
-
A.
\(\Delta CED\)
-
B.
\(\Delta HMN\)
-
C.
\(\Delta CHD\)
-
D.
\(\Delta CNH\)
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 30cm\) và \(AC = 40cm\), đường cao \(AH\), trung tuyến \(AM\).
Tính \(BH,\,\,HM,\,\,MC.\)
-
A.
\(BH = 18cm\,\,;\,\,\,HM = 7cm\,\,;\,\,\,MC = 25cm\)
-
B.
\(BH = 12cm\,\,;\,\,\,HM = 8cm\,\,;\,\,\,MC = 20cm\)
-
C.
\(BH = 16cm\,\,;\,\,\,HM = 8cm\,\,;\,\,\,MC = 24cm\)
-
D.
\(BH = 16cm\,\,;\,\,\,HM = 6cm\,\,;\,\,\,MC = 22cm\)
Tính \(AH.\)
-
A.
\(AH = 18cm\)
-
B.
\(AH = 22cm\)
-
C.
\(AH = 24cm\)
-
D.
\(AH = 28cm\)
Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.
-
A.
\(150c{m^2}\)
-
B.
\(300c{m^2}\)
-
C.
\(125c{m^2}\)
-
D.
\(200c{m^2}\)
Cho \(\Delta ABC\) cân tại \(A\), kẻ đường cao \(AH\) và \(CK\) . Biết \(AH = 7,5cm;\,\,\,CK = 12cm.\) Tính \(BC,AB\).
-
A.
\(AB = 10,5cm\,\,;\,\,\,BC = 18cm\)
-
B.
\(AB = 12cm\,\,;\,\,\,BC = 22cm\)
-
C.
\(AB = 12,5cm\,\,;\,\,\,BC = 20cm\)
-
D.
\(AB = 15cm\,\,;\,\,\,BC = 24cm\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Gọi \(M,N\) theo thứ tự là trung điểm của \(AB,AC\). Biết \(HM = 15cm,HN = 20cm\). Tính \(HB,HC,AH\).
-
A.
\(HB = 12cm\,\,;\,\,\,HC = 28cm\,\,;\,\,\,AH = 20cm\)
-
B.
\(HB = 15cm\,\,;\,\,\,HC = 30cm\,\,;\,\,\,AH = 20cm\)
-
C.
\(HB = 16cm\,\,;\,\,\,HC = 30cm\,\,;\,\,\,AH = 22cm\)
-
D.
\(HB = 18cm\,\,;\,\,\,HC = 32cm\,\,;\,\,\,AH = 24cm\)
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 6cm\) và \(AC = 8cm\) . Các phân giác trong và ngoài của góc \(B\) cắt đường thẳng \(AC\) lần lượt tại \(M\) và \(N\). Tính các đoạn thẳng \(AM\) và \(AN\).
-
A.
\(AM = 3cm\,\,;\,\,\,AN = 9cm\)
-
B.
\(AM = 2cm\,\,;\,\,\,AN = 18cm\)
-
C.
\(AM = 4cm\,\,;\,\,\,AN = 9cm\)
-
D.
\(AM = 3cm\,\,;\,\,\,AN = 12cm\)
Một tam giác vuông có cạnh huyền bằng \(5\), còn đường cao tương ứng cạnh huyền là \(2.\) Hãy tính cạnh nhỏ nhất của tam giác vuông này.
-
A.
\(\sqrt 5\)
-
B.
\(\sqrt 3\)
-
C.
\(1 \)
-
D.
\(2\)
Cho \(\Delta ABC\) vuông tại \(A,\) các cạnh \(AB,\,\,AC\) tương ứng tỉ lệ với \(3\) và \(4.\) Biết đường cao \(AH = 18\,\,cm.\)
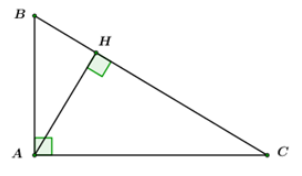
Tính chu vi \(\Delta ABC\).
-
A.
\(90cm\)
-
B.
\(91cm\)
-
C.
\(89cm\)
-
D.
\(88cm\)
Tính diện tích \(\Delta ABC\)
-
A.
\(337cm^2\)
-
B.
\(337,5cm^2\)
-
C.
\(338cm^2\)
-
D.
\(336cm^2\)
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 3cm,\,AC = 4cm,\,\) đường cao \(AH\) và đường trung tuyến \(AM\). Độ dài đoạn thẳng \(HM\) là
-
A.
\(HM = \dfrac{7}{{10}}cm\)
-
B.
\(HM = \dfrac{9}{5}cm\)
-
C.
\(HM = \dfrac{{43}}{{10}}cm\)
-
D.
\(HM = \dfrac{5}{2}cm\)
Cho tam giác \(ABC\) vuông tại \(A\) , đường cao \(AH\) . Biết \(AB = 10cm;\,AH = 6cm\). Tính độ dài các cạnh \(AC,BC\) của tam giác \(ABC\).
-
A.
\(AC = 6,5\,\left( {cm} \right);\,\,\,\,BC = 12\,\left( {cm} \right).\)
-
B.
\(AC = 7,5\,\left( {cm} \right);\,\,\,\,BC = 12,5\,\left( {cm} \right).\)
-
C.
\(AC = 8\,\left( {cm} \right);\,\,\,\,BC = 13\,\left( {cm} \right).\)
-
D.
\(AC = 8,5\,\left( {cm} \right);\,\,\,\,BC = 14,5\,\left( {cm} \right).\)
Lời giải và đáp án
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng?
-
A.
$A{H^2} = AB.AC$
-
B.
$A{H^2} = BH.CH$
-
C.
$A{H^2} = AB.BH$
-
D.
$A{H^2} = CH.BC$
Đáp án : B
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Khi đó ta có hệ thức $H{A^2} = HB.HC$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là sai?
-
A.
$A{B^2} = BH.BC$
-
B.
$A{C^2} = CH.BC$
-
C.
$AB.AC = AH.BC$
-
D.
$A{H^2} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}}$
Đáp án : D
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Khi đó ta có các hệ thức
$A{C^2} = CH.BC$; $A{B^2} = BH.BC$; $AB.AC = BC.AH$và $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
Nhận thấy phương án D: $A{H^2} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$ là sai.
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = 7,2;y = 11,8$
-
B.
$x = 7;y = 12$
-
C.
$x = 7,2;y = 12,8$
-
D.
$x = 7,2;y = 12$
Đáp án : C
Tính $x$ theo hệ thức lượng $A{B^2} = BH.BC$ từ đó suy ra $y$.
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$A{B^2} = BH.BC \Leftrightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{144}}{{20}} = 7,2$$ \Rightarrow CH = BC - BH = 20 - 7,2 = 12,8$
Vậy $x = 7,2;y = 12,8$
Tính $x$ trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai)
-
A.
$x \approx 8,81$
-
B.
$x \approx 8,82$
-
C.
$x \approx 8,83$
-
D.
$x \approx 8,80$
Đáp án : B
Tính $x$ theo hệ thức lượng $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
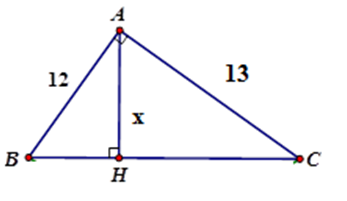
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $ABC$ ta có:
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
\( \Leftrightarrow \dfrac{1}{{A{H^2}}} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} \)\(\Leftrightarrow A{H^2} = \dfrac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2} }}\)
$ \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{12.13}}{{\sqrt {{{12}^2} + {{13}^2}} }} \approx 8,82$
Vậy $x \approx 8,82$.
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = 3,6;y = 6,4$
-
B.
$y = 3,6;x = 6,4$
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Đáp án : A
Bước 1: Tính $BC$ theo định lý Pytago
Bước 2: Tính $x,y$ theo hệ thức lượng $A{B^2} = BH.BC;A{C^2} = CH.BC$
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 100 \Leftrightarrow BC = 10$
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} $
$= \dfrac{{{6^2}}}{10} = 3,6$ hay $x = 3,6$
$ \Rightarrow CH = BC - BH $$= 10 - 3,6 = 6,4.$
hay $y = 6,4$.
Vậy $x = 3,6;y = 6,4.$
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
-
B.
$y = \dfrac{{35\sqrt {74} }}{{74}};x= \sqrt {74} $
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Đáp án : A
Bước 1: Tính $BC$ theo định lý Pytago
Bước 2: Tính $x,y$ theo hệ thức lượng $AH.BC = AB.AC$
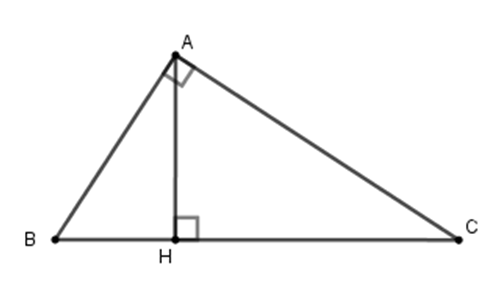
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 74 \Leftrightarrow BC = \sqrt {74} $
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{5.7}}{{\sqrt {74} }} = \dfrac{{35\sqrt {74} }}{{74}}$
Vậy $x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
Cho tam giác $ABC$ vuông tại $A$, $AH \bot BC$( $H$ thuộc $BC$ ). Cho biết $AB:AC = 3:4$ và $BC = 15cm.$ Tính độ dài đoạn thẳng $BH$.
-
A.
$BH = 5,4$
-
B.
$BH = 4,4$
-
C.
$BH = 5,2$
-
D.
$BH = 5$
Đáp án : A
Bước 1: Sử dụng tính chất dãy tỉ số bằng nhau để tìm $AB,AC$. $\left( {\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}}} \right)$
Bước 2: Tính $BH$ theo hệ thức $A{B^2} = BH.BC$
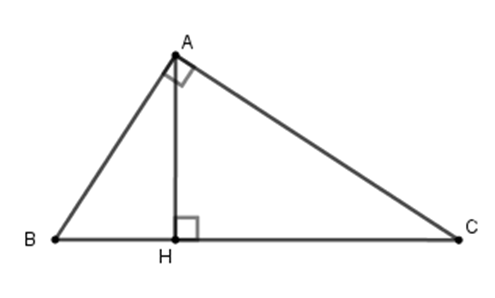
Ta có $AB:AC = 3:4$$ \Leftrightarrow \dfrac{{AB}}{3} = \dfrac{{AC}}{4} \Rightarrow \dfrac{{A{B^2}}}{9} = \dfrac{{A{C^2}}}{{16}} $$= \dfrac{{A{B^2} + A{C^2}}}{{9+16}}= \dfrac{{A{B^2} + A{C^2}}}{{25}}$ $=\dfrac{{B{C^2}}}{{25}}$$= \dfrac{{225}}{{25}} = 9$
(Vì theo định lý Pytago ta có $A{B^2} + A{C^2} = B{C^2} \Leftrightarrow A{B^2} + A{C^2} = 225$)
Nên $\dfrac{{A{B^2}}}{9} = 9 \Rightarrow AB = 9$; $\dfrac{{A{C^2}}}{{16}} = 9 \Rightarrow AC = 12$
Theo hệ thức lượng trong tam giác vuông $ABC$ ta có $A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{81}}{{15}} = 5,4$
Vậy $BH = 5,4$.
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH.$ Cho biết $AB:AC = 3:4$ và $AH = 6cm.$ Tính độ dài các đoạn thẳng $CH.$
-
A.
$CH = 8$
-
B.
$CH = 6$
-
C.
$CH = 10$
-
D.
$CH = 12$
Đáp án : A
Bước 1: Tính $AB,AC$ dựa vào tỉ lệ cho trước và hệ thức $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
Bước 2: Tính $CH$ theo định lý Pytago
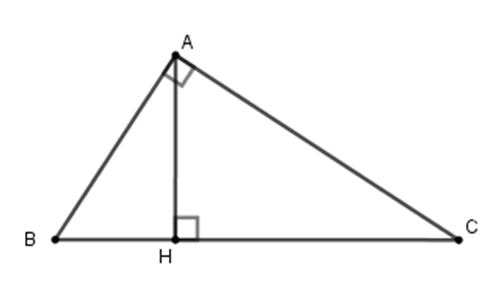
Ta có $AB:AC = 3:4$ , đặt $AB = 3a;AC = 4a\,\left( {a > 0} \right)$
Theo hệ thức lượng $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$$ \Rightarrow \dfrac{1}{{36}} = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{16{a^2}}} \Rightarrow \dfrac{1}{{36}} = \dfrac{{25}}{{144{a^2}}} \Rightarrow a = \dfrac{5}{2}$ (TM )
$ \Rightarrow AB = 7,5;AC = 10$
Theo định lý Pytago cho tam giác vuông $AHC$ ta có $CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {100 - 36} = 8$
Vậy $CH = 8$.
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = 2\sqrt 5 ;y = \sqrt 5 $
-
B.
$x = \sqrt 5 ;y = 3\sqrt 5 $
-
C.
$x = \sqrt 5 ;y = 2\sqrt 5 $
-
D.
$x = 2\sqrt 5 ;y = 2\sqrt 5 $
Đáp án : C
Bước 1: Tính $AH$ theo hệ thức $A{H^2} = BH.CH$
Bước 2: Tính $x;y$ theo định lý Pytago
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$A{H^2} = BH.CH$$ \Rightarrow A{H^2} = 1.4 \Rightarrow AH = 2$
Áp dụng định lý Pytago cho tam giác vuông $AHB;AHC$ ta có
$AB = \sqrt {A{H^2} + H{B^2}} = \sqrt 5 ;AC = \sqrt {A{H^2} + H{C^2}} = 2\sqrt 5 $
Vậy $x = \sqrt 5 ;y = 2\sqrt 5 $.
Tính $x$ trong hình vẽ sau:
-
A.
$x = 6\sqrt 2 $
-
B.
$x = 6$
-
C.
$x = 6\sqrt 3 $
-
D.
$x = \sqrt {82} $
Đáp án : A
Sử dụng hệ thức $\dfrac{1}{{M{D^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}$
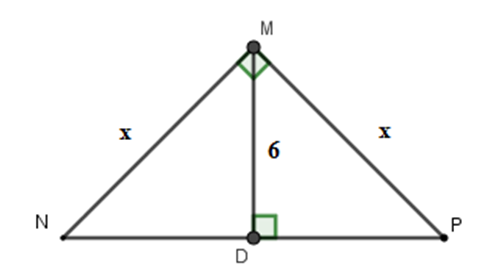
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$\dfrac{1}{{M{D^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}$$ \Rightarrow \dfrac{1}{{36}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^2}}} \Leftrightarrow \dfrac{1}{{36}} = \dfrac{2}{{{x^2}}} \Rightarrow {x^2} = 72 \Leftrightarrow x = 6\sqrt 2 $
Vậy $x = 6\sqrt 2 $.
Cho ABCD là hình thang vuông tại $A$ và $D.$Đường chéo $BD$ vuông góc với $BC.$ Biết $AD = 12cm,DC = 25cm$ . Tính độ dài $BC$, biết $BC < 20$
-
A.
$BC = 15\,cm$
-
B.
$BC = 16\,cm$
-
C.
$BC = 14\,cm$
-
D.
$BC = 17\,cm$
Đáp án : A
Bước 1: Kẻ thêm đoạn $BE \bot CD$ tại $E$
Bước 2: Sử dụng hệ thức giữa cạnh và đường cao để tính $EC$
Bước 3: Áp dụng định lý Pytago để tính $BC$.
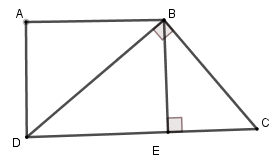
Kẻ $BE \bot CD$ tại $E$
Suy ra tứ giác $ABED$ là hình chữ nhật (vì $\widehat A = \widehat D = \widehat E = 90^\circ $) nên $BE = AD = 12\,\,cm$
Đặt $EC = x\,\left( {0 < x < 25} \right)$ thì $DE = 25 - x$
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $BCD$ ta có
$B{E^2} = ED.EC \Leftrightarrow x\left( {25 - x} \right) = 144 $$\Leftrightarrow {x^2} - 25x + 144 = 0$ \( \Leftrightarrow {x^2} - 16x - 9x + 144 = 0 \)\(\Leftrightarrow x\left( {x - 16} \right) - 9\left( {x - 16} \right) = 0\)$\Leftrightarrow \left( {x - 16} \right)\left( {x - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 16\\x = 9\end{array} \right.$(thỏa mãn)
Với $EC = 16$, theo định lý Pytago ta có $BC = \sqrt {B{E^2} + E{C^2}} = \sqrt {{{12}^2} + {{16}^2}} = 20$ (loại)
Với $EC = 9$, theo định lý Pytago ta có $BC = \sqrt {B{E^2} + E{C^2}} = \sqrt {{{12}^2} + {9^2}} = 15$ (nhận)
Vậy $BC = 15\,cm$.
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB:AC = 3:4\) và \(AB + AC = 21cm\).
Tính các cạnh của tam giác \(ABC\).
-
A.
$AB = 9;AC = 10;BC = 15$
-
B.
$AB = 9;AC = 12;BC = 15$
-
C.
$AB = 8;AC = 10;BC = 15$
-
D.
$AB = 8;AC = 12;BC = 15$
Đáp án: B
Bước 1: Sử dụng tính chất tỉ lệ thức để tìm $AB,AC$. $\left( {\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}}} \right)$
Bước 2: Tính $BC$ theo định lý Pytago
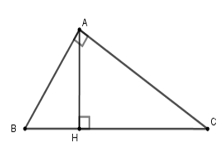
Theo giả thiết: \(AB:AC = 3:4\),
suy ra \(\dfrac{{AB}}{3} = \dfrac{{AC}}{4} = \dfrac{{AB + AC}}{{3 + 4}} = 3\). Do đó \(AB = 3.3 = 9\)\(\left( {cm} \right)\); \(AC = 3.4 = 12\left( {cm} \right)\).
Tam giác \(ABC\) vuông tại \(A\), theo định lý Py-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2} \)\(= {9^2} + {12^2} = 225\), suy ra \(BC = 15cm\).
Tính độ dài các đoạn \(AH,BH,CH\).
-
A.
$BH = 7,2;AH = 5,4;CH = 9,6$
-
B.
$CH = 7,2;BH = 5,4;AH = 9,6$
-
C.
$AH = 7,2;BH = 5,4;CH = 9$
-
D.
$AH = 7,2;BH = 5,4;CH = 9,6$
Đáp án: D
Sử dụng các hệ thức giữa cạnh và đường cao trong tam giác vuông: \(A{B^2} = BH.BC\) và $AH.BC = AB.AC$
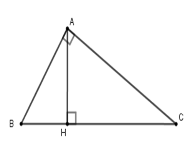
Ta có $AB = 9;AC = 12;BC = 15$
$ \Rightarrow AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}$$ = \dfrac{{12.9}}{{15}} = 7,2$ $A{B^2} = BH.BC \Rightarrow BH $$= \dfrac{{A{B^2}}}{{BC}} $$= \dfrac{{81}}{{15}} = 5,4$
$ \Rightarrow CH = BC - BH = 15 - 5,4 = 9,6$
Vậy $AH = 7,2;BH = 5,4;CH = 9,6$.
Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB, AC.$(hình vẽ)
Tỉ số $\dfrac{{A{B^2}}}{{A{C^2}}}$ bằng với tỉ số nào sau đây?
-
A.
$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HC}}{{HB}}$
-
B.
$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HB}}{{HC}}$
-
C.
$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HA}}{{HB}}$
-
D.
$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HC}}{{HA}}$
Đáp án: B
Xét tam giác vuông $ABC$ có $AH$ là đường cao nên $A{B^2} = BH.BC;A{C^2} = CH.BC$
Nên $\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{BH.BC}}{{CH.BC}} = \dfrac{{HB}}{{HC}}$
Tỉ số $\dfrac{{A{B^3}}}{{A{C^3}}}$ bằng với tỉ số nào sau đây?
-
A.
$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{BD}}{{EC}}$
-
B.
$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{AD}}{{EC}}$
-
C.
$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{BD}}{{ED}}$
-
D.
$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{EC}}{{BD}}$
Đáp án: A
Tam giác vuông $AHB$ có $B{H^2} = BD.AB \Rightarrow BD = \dfrac{{B{H^2}}}{{AB}}$
Tam giác vuông $AHC$ có $H{C^2} = AC.EC \Rightarrow EC = \dfrac{{H{C^2}}}{{AC}}$
Từ đó $\dfrac{{BD}}{{EC}} = \dfrac{{H{B^2}}}{{AB}}:\dfrac{{H{C^2}}}{{AC}} = \dfrac{{H{B^2}}}{{H{C^2}}}.\dfrac{{AC}}{{AB}}$ mà theo câu trước thì $\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HB}}{{HC}}$ nên $\dfrac{{BD}}{{EC}} = \dfrac{{A{B^4}}}{{A{C^4}}}.\dfrac{{AC}}{{AB}} \Leftrightarrow \dfrac{{BD}}{{EC}} = \dfrac{{A{B^3}}}{{A{C^3}}}$
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Cho biết $BH = 4cm,CH = 9cm$. Gọi $D,E$ lần lượt là hình chiếu vuông góc của $H$ trên các cạnh $AB$ và $AC$. Các đường thẳng vuông góc với $DE$ tại $D$ và $E$ lần lượt cắt $BC$ tại $M,N$ . (hình vẽ)
Tính độ dài đoạn thẳng $DE$.
-
A.
$DE = 5\,cm$
-
B.
$DE = 8\,cm$
-
C.
$DE = 7\,cm$
-
D.
$DE = 6\,cm$
Đáp án: D
Bước 1: Chứng minh $DE = AH$
Bước 2: Sử dụng hệ thức $A{H^2} = BH.CH$ từ đó tính $AH$$ \Rightarrow DE$.
Tứ giác $AEHD$ là hình chữ nhật vì $\widehat A = \widehat E = \widehat D = 90^\circ $ nên $DE = AH$
Xét $\Delta ABC$ vuông tại $A$ có $A{H^2} = HB.HC$$ = 4.9 = 36 \Rightarrow AH = 6$
Nên $DE = 6\,cm$.
Kết luận nào sau đây là đúng?
-
A.
\(MN = \dfrac{1}{3}BC\)
-
B.
\(MN = \dfrac{1}{2}BC\)
-
C.
\(MN = \dfrac{3}{4}BC\)
-
D.
\(MN = \dfrac{2}{3}BC\)
Đáp án: B
Chứng minh $M$ là trung điểm của $BH$, $N$ là trung điểm của $CH$
+) Ta có $\widehat {NEC} + \widehat {AED} = 90^\circ $ mà $\widehat {AED} = \widehat {HAE}$ (do $AEHD$ là hình chữ nhật) và $\widehat {HAE} = \widehat {ABC}$ (cùng phụ với $\widehat {ACB}$) nên $\widehat {NEC} + \widehat {ABC} = 90^\circ $ mà $\widehat {ACB} + \widehat {ABC} = 90^\circ $ nên $\widehat {ACB} = \widehat {NEC}$ hay $\Delta NEC$ cân tại $N$$ \Rightarrow EN = NC$.$\left( 1 \right)$
+) $\widehat {NEC} + \widehat {HEN} = 90^\circ $ mà $\widehat {NEC} = \widehat {NCE} \Rightarrow \widehat {NCE} + \widehat {HEN} = 90^\circ $, lại có $\widehat {NCE} + \widehat {NHE} = 90^\circ $ nên $\widehat {NEH} = \widehat {NHE}$ hay $\Delta NEH$ cân tại $N$ suy ra $NE = NH$, $\left( 2 \right)$
Từ $\left( 1 \right);\left( 2 \right)$ ta có $NH = NC$
Tương tự ta có $MH = MB$ nên $MN = MH + NH = \dfrac{1}{2}HB + \dfrac{1}{2}HC = \dfrac{1}{2}BC$.
Tính diện tích tứ giác $DENM$
-
A.
\({S_{DENM}} = 19,5\,c{m^2}\)
-
B.
\({S_{DENM}} = 20,5\,c{m^2}\)
-
C.
\({S_{DENM}} = 19\,c{m^2}\)
-
D.
\({S_{DENM}} = 21,5\,c{m^2}\)
Đáp án: A
Bước 1 : Chứng minh $DENM$ là hình thang vuông
Bước 2: Sử dụng công thức tính diện tích hình thang .
Vì $DM \bot DE;$$EN \bot DE \Rightarrow DM{\rm{//}}EN;$$\widehat D = \widehat E = 90^\circ $ nên $DENM$ là hình thang vuông
Theo kết quả hai câu trước ta có: $DM = \dfrac{{BH}}{2} = 2;$$EN = \dfrac{{CH}}{2} = 4,5;DE = 6$
Nên ${S_{DENM}} = \dfrac{{\left( {DM + EN} \right).DE}}{2} $$= 19,5\,c{m^2}$
Cho tam giác $CDE$ nhọn, đường cao $CH.$ Gọi $M,N$ theo thứ tự là hình chiếu của $H$ lên $CD,CE.$ (hình vẽ)
Tích $CD.CM$ bằng
-
A.
\(CH.CE\)
-
B.
\(CE.CN\)
-
C.
\(CH.CN\)
-
D.
\(CD.CN\)
Đáp án: B
Tam giác $CHD$ vuông tại $H$, ta có $C{H^2} = CM.CD$
Tam giác $CHE$ vuông tại $H$, ta có $C{H^2} = CN.CE$
Nên $CM.CD = CN.CE$.
Tam giác $CMN$ đồng dạng với tam giác nào dưới đây?
-
A.
\(\Delta CED\)
-
B.
\(\Delta HMN\)
-
C.
\(\Delta CHD\)
-
D.
\(\Delta CNH\)
Đáp án: A
Chứng minh tam giác đồng dạng bằng cách sử dụng trường hợp đồng dạng thứ hai cạnh-góc-cạnh
Từ câu trước ta có $CM.CD = CN.CE $$\Leftrightarrow \dfrac{{CM}}{{CN}} = \dfrac{{CE}}{{CD}}$
Xét $\Delta CMN$ và $\Delta CED$ có $\widehat C$ chung và $\dfrac{{CM}}{{CN}} = \dfrac{{CE}}{{CD}}$ nên $\Delta CMN\backsim\Delta CED\,\,\left( {c - g - c} \right)$
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 30cm\) và \(AC = 40cm\), đường cao \(AH\), trung tuyến \(AM\).
Tính \(BH,\,\,HM,\,\,MC.\)
-
A.
\(BH = 18cm\,\,;\,\,\,HM = 7cm\,\,;\,\,\,MC = 25cm\)
-
B.
\(BH = 12cm\,\,;\,\,\,HM = 8cm\,\,;\,\,\,MC = 20cm\)
-
C.
\(BH = 16cm\,\,;\,\,\,HM = 8cm\,\,;\,\,\,MC = 24cm\)
-
D.
\(BH = 16cm\,\,;\,\,\,HM = 6cm\,\,;\,\,\,MC = 22cm\)
Đáp án: A
Sử dụng định lý Pitago, hệ thức lượng trong tam giác vuông và tính chất đường trung tuyến của tam giác để tính các cạnh tương ứng.
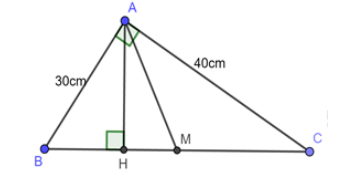
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = {30^2} + {40^2} = 2500 \Rightarrow BC = 50\,\,cm.\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\) \( \Leftrightarrow {30^2} = 50.BH \Leftrightarrow BH = 18\,\,cm.\)
Vì \(AM\) là đường trung tuyến \( \Rightarrow M\) là trung điểm \(BC\)\( \Rightarrow BM = MC = \dfrac{1}{2}BC = \dfrac{1}{2}.50 = 25\,\,cm.\)
Ta có: \(MH = BM - BH = 25 - 18 = 7\,\,cm.\)
Tính \(AH.\)
-
A.
\(AH = 18cm\)
-
B.
\(AH = 22cm\)
-
C.
\(AH = 24cm\)
-
D.
\(AH = 28cm\)
Đáp án: C
Sử dụng hệ thức lượng: \(AH.BC = AB.AC.\)
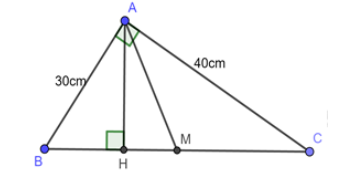
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.50 = 30.40 \Leftrightarrow AH = 24\,\,cm.\)
Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.
-
A.
\(150c{m^2}\)
-
B.
\(300c{m^2}\)
-
C.
\(125c{m^2}\)
-
D.
\(200c{m^2}\)
Đáp án : A
Sử dụng định lý Pytago tính \(HD\)
Sử dụng hệ thức lượng trong tam giác vuông tính \(DE.\)
Diện tích hình thang bằng tích của tổng hai đáy với chiều cao chia 2.
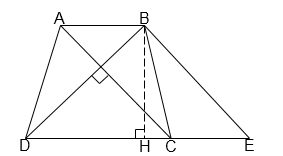
Qua B vẽ đường thẳng song song với \(AC\) , cắt \(DC\) ở \(E\) . Gọi \(BH\) là đường cao của hình thang. Ta có \(BE//AC,AC \bot BD\) nên \(BE \bot BD\)
Áp dụng định lý Pitago vào tam giác vuông \(BDH\) , ta có: \(B{H^2} + H{D^2} = B{D^2}\)
\( \Rightarrow {12^2} + H{D^2} = {15^2} \Rightarrow H{D^2} = 81 \Rightarrow HD = 9cm\)
Xét tam giác \(BDE\) vuông tại \(B\):
\(B{D^2} = DE.DH \Rightarrow {15^2} = DE.9 \Rightarrow DE = 25(cm)\)
Ta có: \(AB = CE\) nên \(AB + CD = CE + CD = DE = 25cm\)
Do đó: \({S_{ABCD}} = 25.12:2 = 150(c{m^2})\)
Cho \(\Delta ABC\) cân tại \(A\), kẻ đường cao \(AH\) và \(CK\) . Biết \(AH = 7,5cm;\,\,\,CK = 12cm.\) Tính \(BC,AB\).
-
A.
\(AB = 10,5cm\,\,;\,\,\,BC = 18cm\)
-
B.
\(AB = 12cm\,\,;\,\,\,BC = 22cm\)
-
C.
\(AB = 12,5cm\,\,;\,\,\,BC = 20cm\)
-
D.
\(AB = 15cm\,\,;\,\,\,BC = 24cm\)
Đáp án : C
Sử dụng định lý Pitago, hệ thức lượng trong tam giác vuông, công thức tính diện tích tam giác và tính chất tam giác cân.
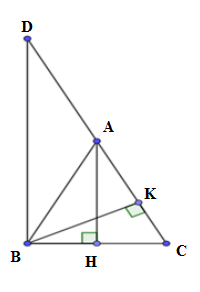
Đặt \(BH = x\,\,\,\,\left( {x > 0,\,\,\,cm} \right)\)
Ta có: \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}CK.AB\)
\(\begin{array}{l} \Leftrightarrow AH.BC = CK.AB\\ \Leftrightarrow 7,5.2x = 12.AB \Leftrightarrow AB = \dfrac{5}{4}x\end{array}\)
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(H\) ta có:
\(A{B^2} = B{H^2} + A{H^2}\) \( \Leftrightarrow \dfrac{{25}}{{16}}{x^2} = {x^2} + 7,{5^2} \Leftrightarrow \dfrac{9}{{16}}{x^2} = 7,{5^2}\)\( \Leftrightarrow {x^2} = 100 \Rightarrow x = 10\)\( \Rightarrow AB = \dfrac{5}{4}.10 = 12,5\,\,cm\)
Ta có: \(\Delta ABC\) cân tại \(A \Rightarrow AH\) là đường cao đồng thời là đường trung tuyến (định lý)
\( \Rightarrow H\) là trung điểm của \(BC\)\( \Rightarrow BC = 2BH = 20cm\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Gọi \(M,N\) theo thứ tự là trung điểm của \(AB,AC\). Biết \(HM = 15cm,HN = 20cm\). Tính \(HB,HC,AH\).
-
A.
\(HB = 12cm\,\,;\,\,\,HC = 28cm\,\,;\,\,\,AH = 20cm\)
-
B.
\(HB = 15cm\,\,;\,\,\,HC = 30cm\,\,;\,\,\,AH = 20cm\)
-
C.
\(HB = 16cm\,\,;\,\,\,HC = 30cm\,\,;\,\,\,AH = 22cm\)
-
D.
\(HB = 18cm\,\,;\,\,\,HC = 32cm\,\,;\,\,\,AH = 24cm\)
Đáp án : D
Sử dụng định lý Pi-ta-go, hệ thức lượng trong tam giác vuông tương ứng để tính độ dài các cạnh.
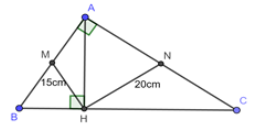
Xét \(\Delta ABH\) vuông tại \(H\) có: \(M\) là trung điểm \(AB\)
\( \Rightarrow HM\) là đường trung tuyến ứng với cạnh huyền \(AB\)
\( \Rightarrow HM = \dfrac{1}{2}AB \Leftrightarrow AB = 2HM = 2.15 = 30\,\,\left( {cm} \right)\)
Xét \(\Delta ACH\) vuông tại \(H\) có: \(N\) là trung điểm \(AC\)
\( \Rightarrow HN\) là đường trung tuyến ứng với cạnh huyền \(AC\)
\( \Rightarrow HN = \dfrac{1}{2}AC \Leftrightarrow AC = 2HN = 2.20 = 40\,\,\left( {cm} \right)\)
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = {30^2} + {40^2} = 2500 \Rightarrow BC = 50\,\,\left( {cm} \right)\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\)\( \Leftrightarrow {30^2} = 50.BH \Leftrightarrow BH = 18\,\,\left( {cm} \right)\)
Ta có: \(HC = BC - BH = 50 - 18 = 32\,\,\left( {cm} \right)\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.50 = 30.40 \Leftrightarrow AH = 24\,\,\left( {cm} \right)\)
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 6cm\) và \(AC = 8cm\) . Các phân giác trong và ngoài của góc \(B\) cắt đường thẳng \(AC\) lần lượt tại \(M\) và \(N\). Tính các đoạn thẳng \(AM\) và \(AN\).
-
A.
\(AM = 3cm\,\,;\,\,\,AN = 9cm\)
-
B.
\(AM = 2cm\,\,;\,\,\,AN = 18cm\)
-
C.
\(AM = 4cm\,\,;\,\,\,AN = 9cm\)
-
D.
\(AM = 3cm\,\,;\,\,\,AN = 12cm\)
Đáp án : D
Sử dụng định lý Pitago cho tam giác ABC vuông tại A để tính độ dài cạnh BC.
Theo đề bài ta có AM, AN lần lượt là các đường phân giác trong và ngoài của góc B.
Khi đó áp dụng tính chất tia phân giác của một góc ta có: \(\dfrac{{AM}}{{MC}} = \dfrac{{AN}}{{NC}} = \dfrac{{AB}}{{BC}}.\)
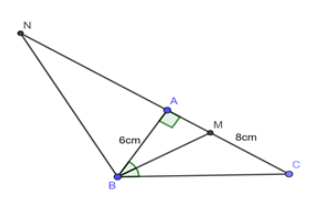
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = 10\left( {cm} \right)\)
Vì \(BM\) là tia phân giác trong của góc \(B \Rightarrow \dfrac{{MA}}{{MC}} = \dfrac{{AB}}{{BC}}\) (Tính chất đường phân giác)
\( \Rightarrow \dfrac{{MA}}{{MC + MA}} = \dfrac{{AB}}{{BC + AB}} \Rightarrow \dfrac{{MA}}{{AC}} = \dfrac{{AB}}{{BC + AB}}\)\( \Rightarrow \dfrac{{MA}}{8} = \dfrac{6}{{10 + 6}} \Rightarrow MA = 3cm\)
Vì \(BM;BN\) là tia phân giác trong và ngoài của góc \(B \Rightarrow \angle NBM = {90^0}\)
Áp dụng hệ thức lượng trong \(\Delta ABM\) vuông tại \(B\) có đường cao \(BA\) ta có:
\( \Rightarrow A{B^2} = AM.AN\)\( \Leftrightarrow {6^2} = 3.AN \Leftrightarrow AN = 12\left( {cm} \right)\)
Một tam giác vuông có cạnh huyền bằng \(5\), còn đường cao tương ứng cạnh huyền là \(2.\) Hãy tính cạnh nhỏ nhất của tam giác vuông này.
-
A.
\(\sqrt 5\)
-
B.
\(\sqrt 3\)
-
C.
\(1 \)
-
D.
\(2\)
Đáp án : A
Giả sử tam giác đã cho là \(\Delta ABC\) vuông tại \(A\) có \(AB < AC,\,\,\,BC = 5,\,\,\,AH = 2.\)
Đặt \(BH = x\,\,\,\left( {0 < x < 2,5} \right).\)
Khi đó áp dụng hệ thức lượng trong tam giác vuông và định lý Pitago để tính \(x\) và từ đó suy ra độ dài các cạnh của tam giác.
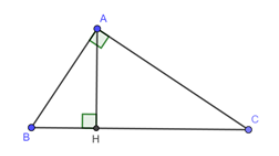
Giả sử tam giác đã cho là \(\Delta ABC\) vuông tại \(A\) có \(AB < AC,\,\,\,BC = 5,\,\,\,AH = 2.\)
Đặt \(BH = x\,\,\,\left( {0 < x < 2,5} \right) \Rightarrow HC = 5 - x.\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\( \Rightarrow A{H^2} = BH.CH \Leftrightarrow {2^2} = x\left( {5 - x} \right)\)
\( \Leftrightarrow {x^2} - 5x + 4 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\left( {tm} \right)\\x = 4\,\,\,\left( {ktm} \right)\end{array} \right.\)
\( \Rightarrow A{B^2} = BC.BH = 5.1 = 5 \Leftrightarrow AB = \sqrt 5 .\)
Vậy cạnh nhỏ nhất của tam giác đã cho có độ dài là \(\sqrt 5 .\)
Cho \(\Delta ABC\) vuông tại \(A,\) các cạnh \(AB,\,\,AC\) tương ứng tỉ lệ với \(3\) và \(4.\) Biết đường cao \(AH = 18\,\,cm.\)
Tính chu vi \(\Delta ABC\).
-
A.
\(90cm\)
-
B.
\(91cm\)
-
C.
\(89cm\)
-
D.
\(88cm\)
Đáp án: A
Sử dụng các công thức hệ thức lượng trong tam giác vuông để tính độ dài các cạnh của \(\Delta ABC\) sau đó áp dụng các công thức tính chu vi tam giác giác để tính.
Theo đề bài ta có: các cạnh \(AB,\,\,AC\) tương ứng tỉ lệ với \(3\) và \(4\)
\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{3}{4} \Leftrightarrow AB = \dfrac{3}{4}AC.\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(\begin{array}{l}\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Leftrightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }}\\ \Leftrightarrow 18 = \dfrac{{\dfrac{3}{4}AC.AC}}{{\sqrt {\dfrac{9}{{16}}A{C^2} + A{C^2}} }} = \dfrac{{\dfrac{3}{4}A{C^2}}}{{\dfrac{5}{4}AC}} = \dfrac{3}{5}AC\\ \Leftrightarrow AC = \dfrac{{18.5}}{3} = 30\,\,cm.\\ \Rightarrow AB = \dfrac{3}{4}AC = \dfrac{3}{4}.30 = 22,5\,\,cm.\end{array}\)
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {22,{5^2} + {{30}^2}} = 37,5\,\,cm.\)
\( \Rightarrow \) Chu vi \(\Delta ABC:\,\,\,AB + BC + CA = 22,5 + 30 + 37,5 = 90\,\,cm.\)
Tính diện tích \(\Delta ABC\)
-
A.
\(337cm^2\)
-
B.
\(337,5cm^2\)
-
C.
\(338cm^2\)
-
D.
\(336cm^2\)
Đáp án: B
Áp dụng các công thức tính diện tích tam giác giác để tính.
Diện tích \(\Delta ABC\) là: \(S = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.18.37,5 = 337,5\,\,c{m^2}.\)
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 3cm,\,AC = 4cm,\,\) đường cao \(AH\) và đường trung tuyến \(AM\). Độ dài đoạn thẳng \(HM\) là
-
A.
\(HM = \dfrac{7}{{10}}cm\)
-
B.
\(HM = \dfrac{9}{5}cm\)
-
C.
\(HM = \dfrac{{43}}{{10}}cm\)
-
D.
\(HM = \dfrac{5}{2}cm\)
Đáp án : A
+) Sử dụng hệ thức lượng trong tam giác vuông tính \(BH\).
+) Tính \(HM = BM - BH\).
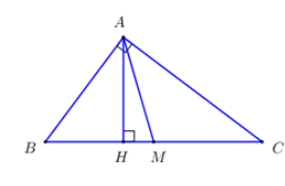
Áp dụng định lí Pytago trong tam giác vuông \(ABC:\,\,BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{3^2} + {4^2}} = 5\,\,\left( {cm} \right)\).
Áp dụng hệ thức lượng trong tam giác vuông \(ABC:\,\,A{B^2} = BC.BH \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{9}{5}\,\,\left( {cm} \right)\).
\(M\) là trung điểm của \(BC \Rightarrow BM = \dfrac{1}{2}BC = \dfrac{5}{2}\,\,\left( {cm} \right)\).
Vậy \( \Rightarrow HM = BM - BH = \dfrac{7}{{10}}\,\,\left( {cm} \right)\)
Cho tam giác \(ABC\) vuông tại \(A\) , đường cao \(AH\) . Biết \(AB = 10cm;\,AH = 6cm\). Tính độ dài các cạnh \(AC,BC\) của tam giác \(ABC\).
-
A.
\(AC = 6,5\,\left( {cm} \right);\,\,\,\,BC = 12\,\left( {cm} \right).\)
-
B.
\(AC = 7,5\,\left( {cm} \right);\,\,\,\,BC = 12,5\,\left( {cm} \right).\)
-
C.
\(AC = 8\,\left( {cm} \right);\,\,\,\,BC = 13\,\left( {cm} \right).\)
-
D.
\(AC = 8,5\,\left( {cm} \right);\,\,\,\,BC = 14,5\,\left( {cm} \right).\)
Đáp án : B
+ Áp dụng định lý Py-ta-go trong tam giác vuông. Tính BH
+ Sử dụng hệ thức lượng trong tam giác. Tính BC
+ Áp dụng định lý Py-ta-go cho tam giác ABC. Tính AC.
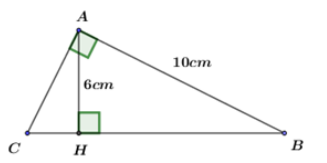
Áp dụng định lý Py-ta-go cho tam giác \(ABH\) vuông tại H. Ta có:
\(\begin{array}{l}A{H^2} + B{H^2} = A{B^2}\\ \Rightarrow B{H^2} = A{B^2} - A{H^2} = {10^2} - {6^2} = 100 - 36 = 64\\ \Rightarrow B{H^2} = {8^2}\\ \Rightarrow BH = 8\,\left( {cm} \right)\end{array}\)
Trong tam giác vuông \(ABC\) vuông tại \(A\) có AH là đường cao
\(\begin{array}{l} \Rightarrow A{B^2} = BH.BC\\ \Rightarrow BC = \dfrac{{A{B^2}}}{{BH}} = \dfrac{{{{10}^2}}}{8} = \dfrac{{100}}{8} = 12,5\,\left( {cm} \right)\end{array}\)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(\begin{array}{l}A{C^2} = B{C^2} - A{B^2} = 12,{5^2} - {10^2} = 56,25\\ \Rightarrow AC = 7,5\,\,\,\,\left( {cm} \right).\end{array}\)
Vậy: \(AC = 7,5\,\left( {cm} \right);\,\,\,\,BC = 12,5\,\left( {cm} \right).\)
Luyện tập và củng cố kiến thức Bài 2: Tỉ số lượng giác của góc nhọn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Ứng dụng thực tế tỉ số lượng giác của góc nhọn Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập hay và khó chương hệ thức lượng trong tam giác vuông Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 5 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 8 Toán 9
- Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9
- Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9
- Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9
- Trắc nghiệm Bài tập ôn tập chương 7 Toán 9
