Bài tập trắc nghiệm Toán lớp 9 có đáp án Bài tập trắc nghiệm Chương 8 Hình trụ - hình nón - hình..

Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9

Đề bài

Xem đáp án

Làm bài tập

Đề bài

Câu 1 :

Cho hình trụ có chu vi đáy là $8\pi $ và chiều cao $h = 10$ . Tính thể tích hình trụ.

A.

$80\pi $
B.

$40\pi $
C.

$160\pi $
D.

$150\pi $

Câu 2 :

Cho hình trụ có bán kính đáy $R = 4\,\left( {cm} \right)$ và chiều cao $h = 5\,\left( {cm} \right)$ . Diện tích xung quanh của hình trụ là

A.

$40\pi $
B.

$30\pi $
C.

$20\pi $
D.

$50\pi $

Câu 3 :

Cho hình trụ có bán kính đáy $R = 8\,cm$ và diện tích toàn phần $564\pi $$c{m^2}$ . Tính chiều cao của hình trụ.

A.

$27\,cm$
B.

$27,25\,cm$
C.

$25\,cm$
D.

$25,27\,cm$

Câu 4 :

Cho hình trụ có bán kính đáy $R$ và chiều cao $h$ . Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì

A.

Thể tích hình trụ không đổi
B.

Diện tích toàn phần không đổi
C.

Diện tích xung quanh không đổi
D.

Chu vi đáy không đổi

Câu 5 :

Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao $h = 12cm$ và đường kính đáy là $d= 8\,cm$ . Tính diện tích các mặt của hộp sữa. Lấy $\pi \approx 3,14$

A.

$110\pi \,\left( {c{m^2}} \right)$
B.

$128\pi \,\left( {c{m^2}} \right)$
C.

$96\pi \,\left( {c{m^2}} \right)$
D.

$112\pi \,\left( {c{m^2}} \right)$

Câu 6 :

Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy $S = 25\pi \,c{m^2}$ và chiều cao $h = 10\,cm$ . Nếu trục lăn đủ $12$ vòng thì diện tích tạo trên sân phẳng là bao nhiêu?

A.

$1200\pi \,\left( {c{m^2}} \right)$
B.

$600\pi \,\left( {c{m^2}} \right)$
C.

$1000\pi \,\left( {c{m^2}} \right)$
D.

$1210\pi \,\left( {c{m^2}} \right)$

Câu 7 :

Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là $3\,cm$ .

A.

$7\,cm$
B.

$5\,cm$
C.

$3\,cm$
D.

$9\,cm$

Câu 8 :

Một hình trụ có thể tích $V$ không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.

A.

$R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}$
B.

$R = \sqrt {\dfrac{V}{{2\pi }}} $
C.

$R = \dfrac{{\sqrt[3]{V}}}{{2\pi }}$
D.

$R = 3\sqrt[3]{{\dfrac{V}{{2\pi }}}}$

Câu 9 :

Cho hình trụ bị cắt bỏ một phần $OABB'A'O'$ như hình vẽ. Thể tích phần còn lại là:

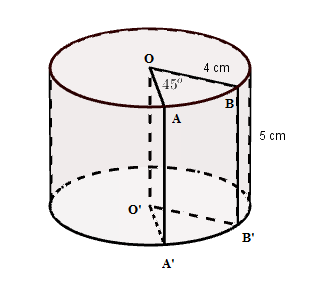
A.

$70\pi \,\,\left( {c{m^3}} \right)$
B.

$80\pi \,\,\left( {c{m^3}} \right)$
C.

$60\pi \,\,\left( {c{m^3}} \right)$
D.

$10\pi \,\,\left( {c{m^3}} \right)$

Cho tam giác $ABC(AB < AC)$ nội tiếp đường tròn $\left( {O;R} \right)$ đường kính $BC.$ Vẽ đường cao $AH$ của tam giác ${\rm{ABC}}{\rm{.}}$ Đường tròn tâm $K$ đường kính $AH$ cắt $AB,AC$ lần lượt tại $D$ và $E.$

Câu 10

Chọn khẳng định sai.

A.

$ADHE$ là hình chữ nhật
B.

$AB.AD = AE.AC.$
C.

$A{H^2} = AD.AB$
D.

$AB.AD = AE.AH$

Câu 11

Biết $BC = 25cm$ và $AH = 12cm.$ Hãy tính diện tích xung quanh của hình tạo thành bởi khi cho tứ giác $ADHE$ quay quanh $AD.$

A.

$\dfrac{{3456}}{5}\pi \left( {c{m^2}} \right)$
B.

$\dfrac{{3456}}{{25}}\pi \left( {c{m^2}} \right)$
C.

$\dfrac{{1728}}{{25}}\pi \left( {c{m^2}} \right)$
D.

$\dfrac{{7128}}{{25}}\pi \left( {c{m^2}} \right)$

Lời giải và đáp án

Câu 1 :

Cho hình trụ có chu vi đáy là $8\pi $ và chiều cao $h = 10$ . Tính thể tích hình trụ.

A.

$80\pi $
B.

$40\pi $
C.

$160\pi $
D.

$150\pi $

Đáp án : C

Phương pháp giải :

Sử dụng công thức tính chu vi đường tròn $C = 2\pi R$ để tính bán kính đáy

Sử dụng công thức tính thể tích hình trụ bán kính $R$ và chiều cao $h$: $V = \pi {R^2}h$

Lời giải chi tiết :

Ta có chu vi đáy $C = 2\pi R = 8\pi$ suy ra $R = 4$

Thể tích hình trụ là $V = \pi {R^2}h = \pi {.4^2}.10 = 160\pi $ (đvtt).

Câu 2 :

Cho hình trụ có bán kính đáy $R = 4\,\left( {cm} \right)$ và chiều cao $h = 5\,\left( {cm} \right)$ . Diện tích xung quanh của hình trụ là

A.

$40\pi $
B.

$30\pi $
C.

$20\pi $
D.

$50\pi $

Đáp án : A

Phương pháp giải :

Sử dụng công thức tính diện tích xung quanh của hình trụ bán kính $R$ và chiều cao $h$

${S_{xq}} = 2\pi Rh$

Lời giải chi tiết :

Diện tích xung quanh của hình trụ là ${S_{xq}} = 2\pi Rh = 2\pi .4.5 = 40\pi \,\,\left( {c{m^2}} \right)$

Câu 3 :

Cho hình trụ có bán kính đáy $R = 8\,cm$ và diện tích toàn phần $564\pi $$c{m^2}$ . Tính chiều cao của hình trụ.

A.

$27\,cm$
B.

$27,25\,cm$
C.

$25\,cm$
D.

$25,27\,cm$

Đáp án : B

Phương pháp giải :

Sử dụng công thức tính diện tích toàn phần của hình trụ ${S_{tp}} = {S_{xq}} + {S_{2d}} = 2\pi Rh + 2\pi {R^2}$ để tính bán kính đáy

Lời giải chi tiết :

Diện tích toàn phần của hình trụ là:

${S_{tp}} = {S_{xq}} + {S_{2d}} = 2\pi Rh + 2\pi {R^2} = 564\pi $

Suy ra $16\pi h + 2\pi {.8^2} = 564\pi$

Do đó $h = 27,25\,(cm)$

Câu 4 :

Cho hình trụ có bán kính đáy $R$ và chiều cao $h$ . Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì

A.

Thể tích hình trụ không đổi
B.

Diện tích toàn phần không đổi
C.

Diện tích xung quanh không đổi
D.

Chu vi đáy không đổi

Đáp án : C

Phương pháp giải :

Sử dụng các công thức tính chu vi đáy, diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ.

Lời giải chi tiết :

Chiều cao mới của hình trụ là $h' = 2h$; bán kính đáy mới là $R' = \dfrac{R}{2}$

Hình trụ mới có:

Chu vi đáy: $2\pi R' = 2\pi \dfrac{R}{2} = \pi R < 2\pi R = C$ nên phương án D sai.

Diện tích toàn phần: $2\pi R'h + 2\pi {R'^2} = 2\pi Rh + \dfrac{{\pi {R^2}}}{2} \ne 2\pi Rh + 2\pi {R^2}$ nên phương án B sai.

Thể tích: $\pi {R'^2}h = \dfrac{{\pi {R^2}h}}{4} \ne \pi {R^2}h$ nên phương án A sai.

Diện tích xung quanh: $2\pi R'h = 2\pi .\dfrac{R}{2}.2h = 2\pi Rh$ nên phương án C đúng.

Câu 5 :

A.

$110\pi \,\left( {c{m^2}} \right)$
B.

$128\pi \,\left( {c{m^2}} \right)$
C.

$96\pi \,\left( {c{m^2}} \right)$
D.

$112\pi \,\left( {c{m^2}} \right)$

Đáp án : D

Phương pháp giải :

Sử dụng công thức tính diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ và diện tích một đáy ${S_d} = \pi {R^2}.$

Lời giải chi tiết :

Bán kính đường tròn đáy $R = \dfrac{8}{2} = 4\,cm$ nên diện tích một đáy ${S_d} = \pi {R^2} = 16\pi \,(c{m^2})$

Ta có diện tích xung quanh của hình trụ: ${S_{xq}} = 2\pi Rh = 2\pi .4.12 = 96\pi \,(c{m^2})$

Vì hộp sữa đã mất nắp nên diện tích các mặt của hộp sữa là:

$96\pi + 16\pi = 112\pi \,\left( {c{m^2}} \right).$

Chú ý

Một số bạn sẽ tính diện tích toàn phần bằng tổng diện tích xung quanh với diện tích hai đáy nhưng hộp sữa ở đây đã mất nắp nên chỉ còn một đáy. Khi tính ta chỉ cần lấy tổng diện tích xung quanh với diện tích một đáy.

Câu 6 :

A.

$1200\pi \,\left( {c{m^2}} \right)$
B.

$600\pi \,\left( {c{m^2}} \right)$
C.

$1000\pi \,\left( {c{m^2}} \right)$
D.

$1210\pi \,\left( {c{m^2}} \right)$

Đáp án : A

Phương pháp giải :

Sử dụng diện tích đáy ${S_{_d}} = \pi {R^2}$ để tính bán kính $R$ .

Sử dụng công thức tính diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$

Lời giải chi tiết :

Bán kính $R$ của đường tròn đáy là $\pi {R^2} = 25\pi $ suy ra $ R = 5\,cm$

Diện tích xung quanh của hình trụ là:

${S_{xq}} = 2\pi Rh = 2\pi .5.10 = 100\pi \left( {c{m^2}} \right)$

Vì trục lăn $12$ vòng nên diện tích tạo trên sân phẳng là $12.100\pi = 1200\pi \,\left( {c{m^2}} \right)$

Câu 7 :

Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là $3\,cm$ .

A.

$7\,cm$
B.

$5\,cm$
C.

$3\,cm$
D.

$9\,cm$

Đáp án : C

Phương pháp giải :

Sử dụng công thức diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ và công thức diện tích toàn phần ${S_{tp}} = 2\pi Rh + 2\pi {R^2}$

Lời giải chi tiết :

Từ giả thiết ta cóL

$2\pi Rh + 2\pi {R^2} = 2.2.\pi Rh$

$Rh = {R^2}$

$R = h$ . Vậy chiều cao của hình trụ là $3\,cm$ .

Câu 8 :

Một hình trụ có thể tích $V$ không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.

A.

$R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}$
B.

$R = \sqrt {\dfrac{V}{{2\pi }}} $
C.

$R = \dfrac{{\sqrt[3]{V}}}{{2\pi }}$
D.

$R = 3\sqrt[3]{{\dfrac{V}{{2\pi }}}}$

Đáp án : A

Phương pháp giải :

Sử dụng công thức diện thể tích của hình trụ $V = \pi {R^2}h$ và công thức diện tích toàn phần ${S_{tp}} = 2\pi Rh + 2\pi {R^2}$

Sử dụng bất đẳng thức Cô-si cho ba số dương $a,b,\,c$ là $a + b + c \ge 3\sqrt[3]{{abc}}$

Dấu “=” xảy ra khi $a = b = c$

Lời giải chi tiết :

Gọi bán kính đáy và chiều cao của hình trụ lần lượt là $R,\,\,h\,\,\left( {R > 0;\,h > 0} \right)$

Ta có $V = \pi {R^2}h$ suy ra $h = \dfrac{V}{{\pi {R^2}}}$

Diện tích toàn phần của hình trụ là:

${S_{tp}} = 2\pi Rh + 2\pi {R^2} = 2\pi R.\dfrac{V}{{\pi {R^2}}} + 2\pi {R^2} = \dfrac{{2V}}{R} + 2\pi {R^2}$

$ = \dfrac{V}{R} + \dfrac{V}{R} + 2\pi {R^2} \ge 3\sqrt[3]{{\dfrac{V}{R}.\dfrac{V}{R}.2\pi {R^2}}} = 3\sqrt[3]{{2\pi {V^2}}}$ (theo bất đẳng thức Cosi)

Dấu “=” xảy ra khi $\dfrac{V}{R} = 2\pi {R^2}$ suy ra $R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}$

Vậy với $R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}$ thì ${S_{tp}}$ đạt giá trị nhỏ nhất là $3\sqrt[3]{{2\pi {V^2}}}$.

Câu 9 :

Cho hình trụ bị cắt bỏ một phần $OABB'A'O'$ như hình vẽ. Thể tích phần còn lại là:

A.

$70\pi \,\,\left( {c{m^3}} \right)$
B.

$80\pi \,\,\left( {c{m^3}} \right)$
C.

$60\pi \,\,\left( {c{m^3}} \right)$
D.

$10\pi \,\,\left( {c{m^3}} \right)$

Đáp án : A

Phương pháp giải :

Dựa vào hình vẽ tính xem phần cắt đi chiếm bao nhiêu phần thể tích hình trụ.

Sử dụng công thức tính thể tích hình trụ $V = \pi R^2h$.

Từ đó suy ra thể tích phần còn lại sau khi cắt.

Lời giải chi tiết :

Phần hình trụ bị cắt đi chiếm $\dfrac{{45^\circ }}{{360^\circ }} = \dfrac{1}{8}$ (hình trụ)

Thể tích phần còn lại là $V = \dfrac{7}{8}\pi {R^2}h = \dfrac{7}{8}\pi {.4^2}.5 = 70\pi \,\,\left( {c{m^3}} \right)$

Câu 10

Chọn khẳng định sai.

A.

$ADHE$ là hình chữ nhật
B.

$AB.AD = AE.AC.$
C.

$A{H^2} = AD.AB$
D.

$AB.AD = AE.AH$

Đáp án: D

Phương pháp giải :

Sử dụng dấu hiệu nhận biết hình chữ nhật và hệ thức lượng trong tam giác vuông

Lời giải chi tiết :

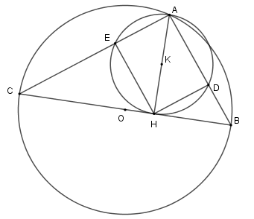
Xét $\left( O \right)$ có $\widehat {CAD} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn)

Xét $\left( K \right)$ có $\widehat {AEH} = \widehat {ADH} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn)

Nên tứ giác $ADHE$ là hình chữ nhật ( vì có ba góc vuông)$ \Rightarrow $ phương án A đúng.

Xét tam giác vuông $AHB$ có $A{H^2} = AD.AB \Rightarrow $ phương án C đúng

Xét tam giác vuông $A{H^2} = AC.AE$ nên $AD.AB = AC.AE \Rightarrow $ phương án B đúng

Câu 11

Biết $BC = 25cm$ và $AH = 12cm.$ Hãy tính diện tích xung quanh của hình tạo thành bởi khi cho tứ giác $ADHE$ quay quanh $AD.$

A.

$\dfrac{{3456}}{5}\pi \left( {c{m^2}} \right)$
B.

$\dfrac{{3456}}{{25}}\pi \left( {c{m^2}} \right)$
C.

$\dfrac{{1728}}{{25}}\pi \left( {c{m^2}} \right)$
D.

$\dfrac{{7128}}{{25}}\pi \left( {c{m^2}} \right)$

Đáp án: B

Phương pháp giải :

Sử dụng hệ thức lượng để tính cạnh $AD,\,HD$

Sử dụng công thức diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$

Lời giải chi tiết :

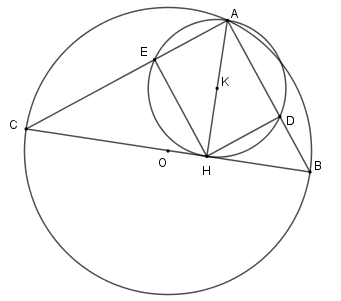
Xét tam giác vuông $ABC$ có $HB.HC = A{H^2} \Leftrightarrow HB.HC = 144$ và $HB + HC = BC \Leftrightarrow HB + HC = 25$

Suy ra $HB = 9\,cm;\,HC = 16\,cm$ (Chú ý: $AB < AC$ nên $HB < HC$).

Xét tam giác vuông $AHB$ có $\dfrac{1}{{H{D^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{H{B^2}}} \Rightarrow HD = \dfrac{{36}}{5}\,cm$

Tương tự ta có $HE = \dfrac{{48}}{5}cm \Rightarrow AD = \dfrac{{48}}{5}\,cm$.

Khi quay hình chữ nhật $ADHE$ quanh $AD$ ta được hình trụ có chiều cao $AD$ và bán kính đáy $HD$.

Nên ${S_{xq}} = 2.\pi HD.AD = \dfrac{{3456}}{{25}}\pi \left( {c{m^2}} \right)$

Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9

Luyện tập và củng cố kiến thức Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9

Luyện tập và củng cố kiến thức Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài tập ôn tập chương 8 Toán 9

Luyện tập và củng cố kiến thức Bài tập ôn tập chương 8 Toán 9 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9

Báo lỗi góp ý