Giải vở bài tập toán lớp 9 tập 1, tập 2 Ôn tập chương 3 - Góc với đường tròn

Bài 55 trang 124 Vở bài tập toán 9 tập 2


Giải bài 55 trang 124 VBT toán 9 tập 2. Trong hình 62, đường tròn tâm O có bán kính R = 2m, góc AOB bằng 75 độ a) Tính số đo cung ApB b) Tính độ dài các cung AqB và ApB...

Đề bài

Trong hình 62, đường tròn tâm \(O\) có bán kính \(R = 2m,\,\,\widehat {AOB} = {75^o}\)

 

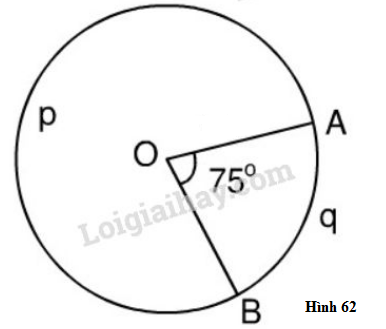
 a) Tính sđ \(\overparen{ApB}\)

b) Tính độ dài các cung \(AqB\) và \(ApB\)

c) Tính diện tích hình quạt tròn \(OAqB\)

Phương pháp giải - Xem chi tiết

a) + Số đo góc ở tâm bằng số đo cung bị chắn

    + Số đo cung lớn bằng \(360^\circ \)\( - \) số đo cung nhỏ.

b) Cho hình tròn bán kính \(R\),  độ dài cung tròn \(n^\circ \) là \(l = \dfrac{{\pi Rn}}{{180}}\)

    Chu vi hình tròn đó là \(C = 2\pi R\)

c) Cho hình tròn bán kính \(R\),  diện tích quạt tròn số đo \(n^\circ \) là \(S = \dfrac{{\pi {R^2}n}}{{360}}\)

Lời giải chi tiết

a) Từ giả thiết \(\widehat {AOB} = 75^\circ \)  \( \Rightarrow \) sđ\(\overparen{AqB}\)\( = 360^\circ  - \) sđ\(\overparen{AB}\)

Vậy  sđ\(\overparen{ApB}\)\( = 360^\circ  - 75^\circ  = 285^\circ \) 

b) Gọi \({l_{\overparen{AqB}}},{l_{\overparen{ApB}}}\) lần lượt là độ dài của các cung \(AqB,ApB;C = 2\pi R\) là độ dài đường tròn tâm \(O.\)

Theo công thức tính độ dài cung ta có : 

\(\displaystyle {l_{\overparen{AqB}}}\) \(=\displaystyle {{\pi Rn} \over {180}} = {{\pi .2.75} \over {180}} = {5 \over 6}\pi (cm)\) 

Vậy  \({l_{\overparen{ApB}}} = C - {l_{\overparen{AqB}}} = 4\pi  - \dfrac{{5\pi }}{6} \)\(= \dfrac{{19\pi }}{6}\left( {cm} \right).\)

c) Ta có \(\widehat{AOB}\) \( = 75^\circ ;R = 2cm\)

Vậy \({S_{OAqB}} = \dfrac{{\pi {{.2}^2}.75}}{{360}} = \dfrac{{5\pi }}{6}\left( {c{m^2}} \right).\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store