Bài 4 trang 200 SBT hình học 11

Giải bài 4 trang 200 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a...

Đề bài

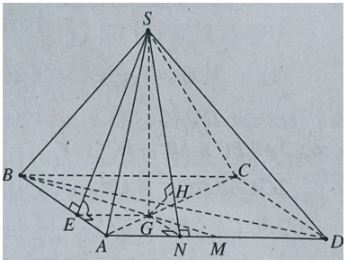
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên đáy ABCD trùng với trọng tâm tam giác ABD. Mặt bên (SAB) tạo với đáy góc 60^ο. Tính theo a khoảng cách từ B đến mặt phẳng (SAD)

Lời giải chi tiết

+ Xác định góc của (SAB) và mặt phẳng đáy.

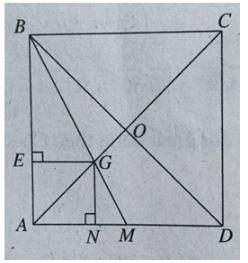
Gọi G là trọng tâm tam giác ABD và E là hình chiếu của G lên AB. Ta có:

AB ⊥ SG & AB ⊥ GE⇒ AB ⊥ (SEG) ⇒ AB ⊥ SE.

SE ⊥ AB & GE ⊥ AB⇒ ∠((SAB),(ABCD)) = ∠(SEG) = 60^o.

+ Xác định khoảng cách từ B đến mặt phẳng (SAD).

Hạ GN ⊥ AD. Tương tự như trên, ta có: AD ⊥ GN & AD ⊥ SG⇒ AD ⊥ (SGN)

Hạ GH ⊥ SN, ta có GH ⊥ (SAD) suy ra khoảng cách từ G đến (SAD) là GH.

+ Tính GH.

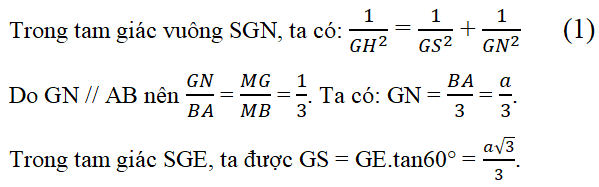
(do GE = GN). Thế vào (1) ta được:

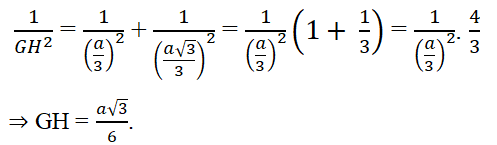
Ta có: M ∈(SAD) & MB = 3MG⇒ d(B,(SAD)) = 3d(G,(SAD)) = (a√3)/2.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 5 trang 200 SBT hình học 11
Giải bài 5 trang 200 sách bài tập hình học 11. Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AB = a√3, ∠BAD = 120o. Góc giữa đường thẳng AC' và mặt phẳng (ADD'A') là 30 o. Gọi M là trung điểm A'D', N là trung điểm BB'. Tính khoảng cách từ N đến mặt phẳng (C'MA)
Bài 6 trang 200 SBT hình học 11
Giải bài 6 trang 200 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30o. Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).
Bài 7 trang 200 SBT hình học 11
Giải bài 7 trang 200 sách bài tập hình học 11. Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông với AB = BC = a, cạnh bên AA' = a√2. Gọi M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM, B'C.
Bài 8 trang 200 SBT hình học 11
Giải bài 8 trang 200 sách bài tập hình học 11. Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a. Gọi E là điểm đối xứng của D qua trung điểm SA, M là trung điểm của AE, N là trung điểm của BC. Chứng minh rẳng MN vuông góc với BD và tính khoảng cách giữa hai đường thẳng MN và AC.
Bài 9 trang 200 SBT hình học 11
Giải bài 9 trang 200 sách bài tập hình học 11. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABC). Gọi M là trung điểm của AB, mặt phẳng qua SM song song với BC cắt AC tại N. Biết góc tạo bởi (SBC) và (ABC) là 60o. Tìm khoảng cách giữa hai đường thẳng AB và SN.
Bài tập trắc nghiệm trang 201, 202, 203, 204, 205 SBT Hình học 11
Giải bài tập trắc nghiệm trang 201, 202, 203, 204, 205 sách bài tập Hình học 11
Bài 3 trang 199 SBT hình học 11
Giải bài 3 trang 199 sách bài tập hình học 11. Cho tứ diện SABC có SA, SB, SC vuông góc với nhau từng đôi một. Gọi H là hình chiếu vuông góc của S lên mp(ABC)...
Bài 2 trang 199 SBT hình học 11
Giải bài 2 trang 199 sách bài tập hình học 11. Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a...
Bài 1 trang 199 SBT hình học 11
Giải bài 1 trang 199 sách bài tập hình học 11. Cho hình chóp tứ giác đều S.ABCD. Gọi H là chân đường cao của hình chóp. Một mặt phẳng (P) thay đổi cắt các cạnh bên SA, SB, SC, SD lần lượt tại E, F, I, J. Gọi K = EI ∩ FJ. Đặt SE = a, SF = b, SI = c, SJ = d, SK = k, ∠ASH = α...