-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 3.54 trang 133 SBT hình học 12
Giải bài 3.54 trang 133 sách bài tập hình học 12. Cho hai đường thẳng ...
Đề bài
Cho hai đường thẳng d: \(\left\{ {\begin{array}{*{20}{c}}{x = 6}\\{y = - 2t}\\{z = 7 + t}\end{array}} \right.\) và d1: \(\left\{ {\begin{array}{*{20}{c}}{x = - 2 + t'}\\{y = - 2}\\{z = - 11 - t'}\end{array}} \right.\)
Lập phương trình mặt phẳng (P) sao cho khoảng cách từ d và d1 đến (P) là bằng nhau.
Phương pháp giải - Xem chi tiết
Nhận xét: Do d và d1 chéo nhau nên (P) là mặt phẳng đi qua trung điểm của đoạn vuông góc chung AB của d, d1 và song song với d và d1.
Lời giải chi tiết
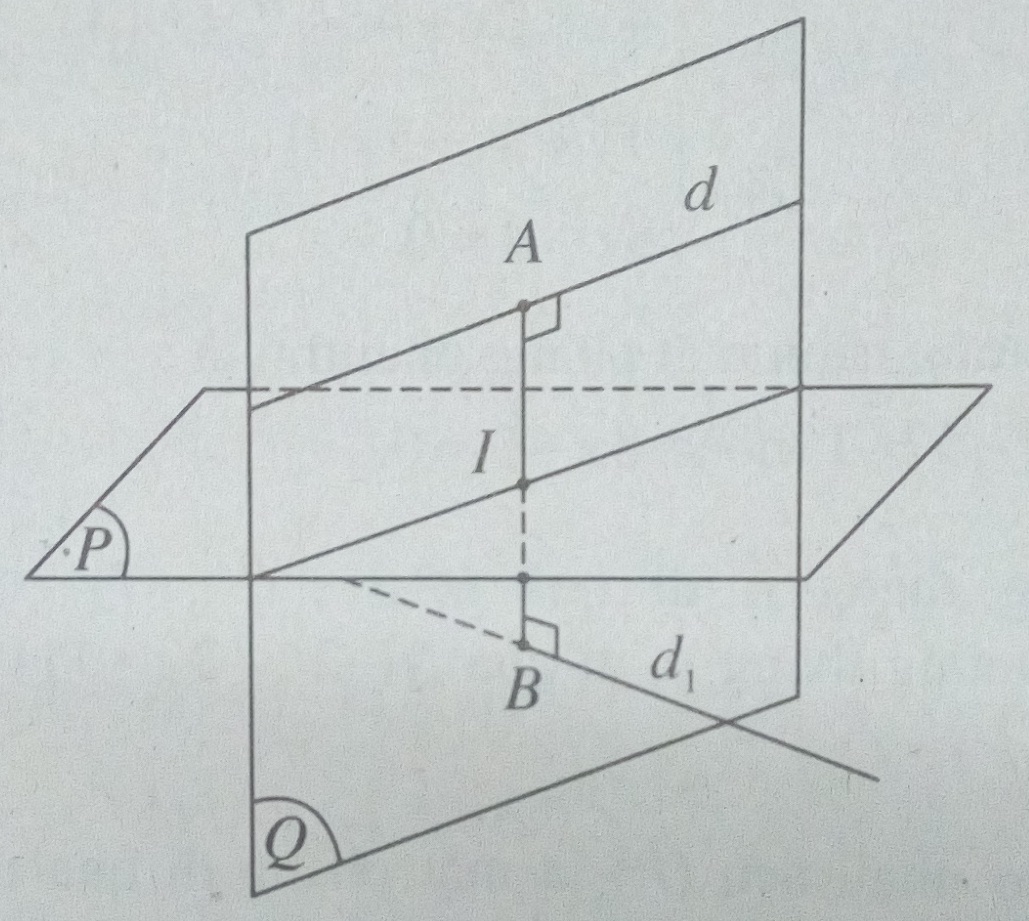
Hình 3.32
Đường thẳng d đi qua M(6; 0 ;7) có vecto chỉ phương \(\overrightarrow a (0; - 2;1)\).
Đường thẳng d1 đi qua N(-2; -2; -11) có vecto chỉ phương \(\overrightarrow b (1;0; - 1)\).
Do d và d1 chéo nhau nên (P) là mặt phẳng trung trực của đoạn vuông góc chung AB của d, d1 và song song với d và d1.
Để tìm tọa độ của A, B ta làm như sau:
Lấy điểm A(6; - 2t; 7 + t) thuộc d, B( -2 + t’; -2 ; -11 – t’) thuộc d1. Khi đó: \(\overrightarrow {AB} = ( - 8 + t'; - 2 + 2t; - 18 - t - t')\)
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AB} \bot \overrightarrow a }\\{\overrightarrow {AB} \bot \overrightarrow b }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AB} .\overrightarrow a = 0}\\{\overrightarrow {AB} .\overrightarrow b = 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 2( - 2 + 2t) + ( - 18 - t - t') = 0}\\{ - 8 + t' - ( - 18 - t - t') = 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 5t - t' - 14 = 0}\\{t + 2t' + 10 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{t = - 2}\\{t' = - 4}\end{array}} \right.\)
Suy ra A(6; 4; 5), B(-6; -2; -7)
Trung điểm của AB là I(0; 1; -1)
Ta có: \(\overrightarrow {AB} = ( - 12; - 6; - 12)\). Chọn \(\overrightarrow {{n_P}} = (2;1;2)\)
Phương trình của (P) là: 2x + (y – 1) + 2(z + 1) = 0 hay 2x + y +2z + 1 = 0.
Chú ý:
Có thể tìm tọa độ của A, B bằng cách khác:
Ta có: Vecto chỉ phương của đường vuông góc chung của d và d1 là là \(\left[ {\overrightarrow a ,\overrightarrow b } \right] = \left( {\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{ - 2}\\0\end{array}}&{\begin{array}{*{20}{c}}1\\{ - 1}\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1\\{ - 1}\end{array}}&{\begin{array}{*{20}{c}}0\\1\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}0\\1\end{array}}&{\begin{array}{*{20}{c}}{ - 2}\\0\end{array}}\end{array}} \right|} \right)\)\( = \left( {2;1;2} \right)\)
Gọi (Q) là mặt phẳng chứa d và đường vuông góc chung AB.
Khi đó: \(\overrightarrow {{n_Q}} = \left[ {\overrightarrow a ,\left[ {\overrightarrow a ,\overrightarrow b } \right]} \right]\)\( = \left( {\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{ - 2}\\1\end{array}}&{\begin{array}{*{20}{c}}1\\2\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1\\2\end{array}}&{\begin{array}{*{20}{c}}0\\2\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}0\\2\end{array}}&{\begin{array}{*{20}{c}}{ - 2}\\1\end{array}}\end{array}} \right|} \right)\) \( = \left( { - 5;2;4} \right)\)
Phương trình của (Q) là : \(–5(x – 6) + 2y + 4(z – 7) = 0\) hay \(–5x + 2y + 4z + 2 = 0\)
Để tìm \({d_1} \cap (Q)\) ta thế phương trình của d1 vào phương trình của (Q). Ta có:
\(–5(–2 + t’) + 2(–2) +4(–11 – t’ ) + 2 = 0\) \( \Rightarrow t' = 4\)
\( \Rightarrow {d_1} \cap \left( Q \right) = B\left( { - 6; - 2; - 7} \right)\)
Tương tự, gọi (R) là mặt phẳng chứa \({d_1}\) và đường vuông góc chung AB.
Khi đó: \(\overrightarrow {{n_R}} = ( - 1;4; - 1)\)
Phương trình của (R) là \( –x + 4y – z – 5 = 0\).
Suy ra \(d \cap (R) = A(6;4;5)\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3.55 trang 133 SBT hình học 12
- Bài 3.56 trang 133 SBT hình học 12
- Bài 3.57 trang 133 SBT hình học 12
- Bài 3.58 trang 133 SBT hình học 12
- Bài 3.59 trang 134 SBT hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
