Bài 7. Vị trí tương đối của hai đường tròn

Bài 32 trang 135 Vở bài tập toán 9 tập 1

Giải bài 32 trang 135 VBT toán 9 tập 1. Cho hai đường tròn đồng tâm O. Dây AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC = BD.

Đề bài

Cho hai đường tròn đồng tâm \(O\). Dây \(AB\) của đường tròn lớn cắt đường tròn nhỏ ở \(C\) và \(D\). Chứng minh rằng \(AC=BD\).

Phương pháp giải - Xem chi tiết

Vẽ đường kính vuông góc với một dây rồi dùng tính chất đường kính vuông góc với một dây thì chia đôi đi qua trung điểm dây ấy.

Lời giải chi tiết

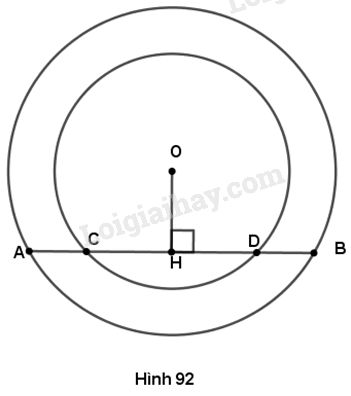
Giả sử \(C\) nằm giữa \(A\) và \(D\) (trường hợp \(D\) nằm giữa \(A\) và \(C\) được chứng minh tương tự).

Kẻ \(OH \bot CD.\) Áp dụng định lí về đường kính vuông góc với dây, ta có :

\(OH \bot AB\) nên \(HA = HB{\rm{ }}\left( 1 \right)\)

\(OH \bot CD\) nên \(HC = HD{\rm{ }}\left( 2 \right)\)

Từ (1) và (2) suy ra \(HA - HC = HB - HD,\) tức là \(AC = BD.\)

Chú ý :

Khi \(D\) nằm giữa \(A\) và \(C\), ta thay dấu – bởi dấu +.

Loigiaihay.com

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Các bài liên quan: - Bài 7. Vị trí tương đối của hai đường tròn

Luyện Bài tập trắc nghiệm môn Toán lớp 9 - Xem ngay

Báo lỗi - Góp ý

>>Học trực tuyến lớp 9, luyện vào lớp 10, mọi lúc, mọi nơi môn Toán, Văn, Anh, Lý, Hóa, Sinh, Sử, Địa cùng các Thầy, Cô giáo giỏi nổi tiếng, dạy hay, dễ hiểu, dày dặn kinh nghiệm tại Tuyensinh247.com