Giải vở bài tập toán lớp 9 tập 1, tập 2 Bài 7. Vị trí tương đối của hai đường tròn

Bài 30 trang 134 Vở bài tập toán 9 tập 1


Giải bài 30 trang 134 VBT toán 9 tập 1. Cho đường tròn (O), đường kính AB = 25cm. Vẽ đường tròn tâ m B bán kính 15cm, cắt đường tròn (O) ở C và D...

Đề bài

Cho đường tròn (O), đường kính AB = 25cm. Vẽ đường tròn tâm B bán kính 15cm, cắt đường tròn (O) ở C và D.

a) Chứng minh rằng AC là tiếp tuyến của đường tròn (B).

b) Tính độ dài AC

c) Gọi H là giao điểm của AB và CD. Tính độ dài AH, HB.

Phương pháp giải - Xem chi tiết

a) Chứng minh \(AC\) có một điểm chung với đường tròn và bán kính vuông góc với \(AC\) tại điểm đó.

b) Áp dụng định lí Py-ta-go vào tam giác vuông.

c) Áp dụng hệ thức lượng trong tam giác vuông \(a = a'.c.\)

Lời giải chi tiết

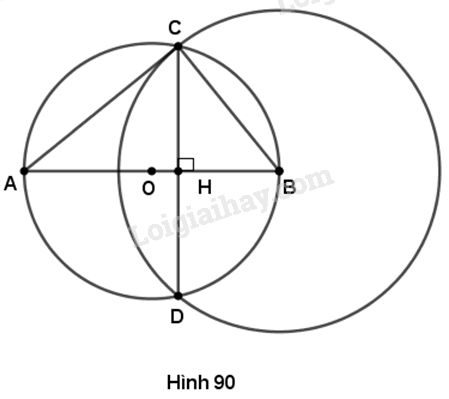
a) Tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AB\) nên \(\widehat {ACB} = {90^o}.\)

\(AC\) vuông góc với bán kính \(BC\) của đường tròn  \(\left( B \right)\) tại \(C\) nên \(AC\) là tiếp tuyến của \(\left( B \right).\)

  b) Áp dụng định lí Py-ta-go vào tam giác vuông \(ACB,\) ta có

\(A{C^2} = A{B^2} - B{C^2} = {25^2} - {15^2} \)\(= 625 - 225 = 400\left( {cm} \right).\)

Suy ra \(AC = 20\left( {cm} \right).\) 

c) Tam giác \(ABC\) vuông tại \(C,\) đường cao \(CH\) nên \(A{C^2} = AB.AH\)

suy ra \({20^2} = 25.AH,\) do đó \(AH = \dfrac{{400}}{{25}} = 16\left( {cm} \right).\)

Tính \(HB,\) ta có \(HB = AB - AH \)\(= 25 - 16 = 9\left( {cm} \right).\) 

Loigiaihay.com


Bình chọn:
4.1 trên 8 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store