Bài 6. Tính chất của hai tiếp tuyến cắt nhau

Bài 27 trang 130 Vở bài tập toán 9 tập 1

Giải bài 27 trang 130 VBT toán 9 tập 1. Cho tam giác ABC vuông tại A ngoại tiếp đường tròn (I)...

Đề bài

Cho tam giác ABC vuông tại A ngoại tiếp đường tròn (I). Gọi các tiếp điểm của đường tròn (I) với AB, AC theo thứ tự là D, E.

a) Tứ giác ADIE là hình gì ? Vì sao ?

b) Tính bán kính của đường tròn (I), biết AB = 13cm, AC = 84cm.

Phương pháp giải - Xem chi tiết

a) Chứng minh tứ giác là hình chữ nhật có một cặp cạnh kề bằng nhau.

b) Dùng tính chất hai tiếp tuyến cắt nhau đề tìm các cặp cạnh bằng nhau; tìm \(AD\) rồi suy ra độ dài của \(DI.\)

Lời giải chi tiết

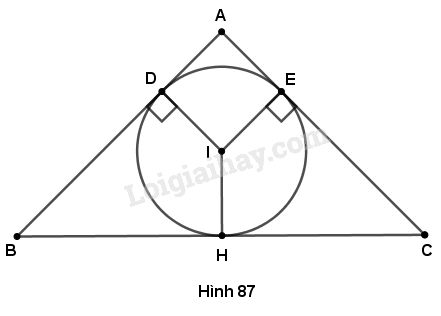
a) Tứ giác \(ADIE\) có \(\widehat A = {90^o}\) (theo giả thiết)

\(\widehat D = {90^o}\) (vì \(AB\) là tiếp tuyến của \(\left( I \right)\))

\(\widehat E = {90^o}\) (vì \(AC\) là tiếp tuyến của \(\left( I \right)\))

Do đó \(ADIE\) là hình chữ nhật.

Hình chữ nhật \(ADIE\) có \(DI = IE\) (bán kính) nên \(ADIE\) là hình vuông.

b) Trước tiên ta tính \(BC:\) Áp dụng định lí Py-ta-go vào tam giác vuông \(ABC\) ta có \(B{C^2} = A{B^2} + A{C^2} \)\(= {13^2} + {84^2} \)\(= 169 + 7056 = 7225.\)

Suy ra \(BC = 85cm.\)

Kẻ \(IH \bot BC,\) ta có \(AB + AC - BC \)\(= \left( {AD + BD} \right) + \left( {AE + EC} \right) - \left( {BH + HC} \right).\)

Ta lại có

\(DB = BH,EC = HC,AE = AD\) nên \(AB + AC - BC = AD + AE = 2AD.\)

Do \(AB = 13cm\) nên \(AB + AC - BC = 2AD\)

Suy ra \(2AD = 13 + 84 - 85 = 12\left( {cm} \right).\)

Do đó \(AD = 6cm.\)

Tứ giác \(ADIE\) là hình vuông (câu a) nên \(ID = AD = 6cm.\)

Vậy bán kính của đường tròn \(\left( I \right)\) bằng \(6cm.\)

Chú ý :

Trong phần b), ta chứng minh một hệ thức tương tự bài 26 để sử dụng.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 5 phiếu

Bài tiếp theo

Bài 26 trang 130 Vở bài tập toán 9 tập 1
Giải bài 26 trang 130 VBT toán 9 tập 1. Trên hình 86, tam giác ABC ngoại tiếp đường tròn (O)...
Bài 25 trang 129 Vở bài tập toán 9 tập 1
Giải bài 25 trang 129 VBT toán 9 tập 1. Cho nửa đường tròn tâm O đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn)...
Bài 24 trang 128 Vở bài tập toán 9 tập 1
Giải bài 24 trang 128 VBT toán 9 tập 1. Cho đường tròn (O), điểm I nằm bên ngoài đường tròn...
Bài 23 trang 128 Vở bài tập toán 9 tập 1
Giải bài 23 trang 128 VBT toán 9 tập 1. Từ một điểm nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC ...
Bài 22 trang 127 Vở bài tập toán 9 tập 1
Giải bài 22 trang 127 VBT toán 9 tập 1. Cho đường tròn (O), điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm)...
Phần câu hỏi bài 6 trang 126, 127 Vở bài tập toán 9 tập 1
Giải phần câu hỏi bài 6 trang 126, 127 VBT toán 9 tập 1. Cho tam giác ABC không là tam giác cân. Ta có:...