Giải SBT toán hình học và đại số giải tích 11 cơ bản

Bài 3: Đường thẳng và mặt phẳng song song

Bài 2.20 trang 71 SBT hình học 11

Giải bài 2.20 trang 71 sách bài tập hình học 11.Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng (α) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q...

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Cho tứ diện \(ABCD\). Qua điểm \(M\) nằm trên \(AC\) ta dựng một mặt phẳng \(\left( \alpha \right)\) song song với \(AB\) và \(CD\). Mặt phẳng này lần lượt cắt các cạnh \(BC\), \(BD\) và \(AD\) tại \(N\), \(P\) và \(Q\).

LG a

Tứ giác \(MNPQ\) là hình gì?

Phương pháp giải:

- Sử dụng tính chất: Cho đường thẳng \(d\) song song với mặt phẳng \((\alpha)\). Nếu mặt phẳng \((\beta)\) chứa \(d\) và cắt \((\alpha)\) theo giao tuyến \(d’\) thì \(d’\parallel d\).

\(\begin{array}{l}\left\{ \begin{array}{l}d\parallel (\alpha )\\d \subset (\beta )\\(\alpha ) \cap (\beta ) = d'\end{array} \right.\\ \Rightarrow d\parallel d'\end{array}\)

Lời giải chi tiết:

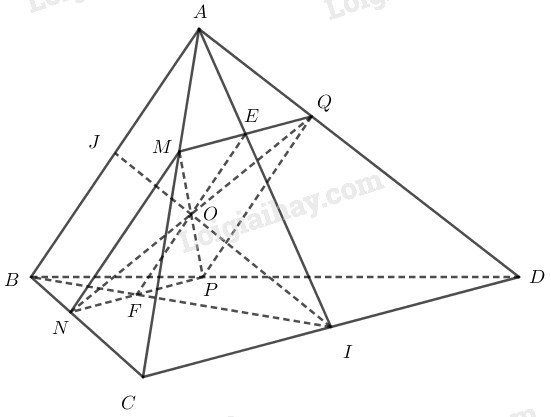
Ta có:

\( \left\{\begin{array}{l}(\alpha )\parallel AB\\AB \subset (ABC)\\(\alpha ) \cap (ABC) = MN\end{array} \right. \)

\(\Rightarrow MN\parallel AB\)

Ta có:

\(\left\{ \begin{array}{l}(\alpha )\parallel CD\\CD \subset (BCD)\\(\alpha ) \cap (BCD) = NP\end{array} \right.\)

\(\Rightarrow CD\parallel NP\)

Ta có:

\(\left\{ \begin{array}{l}(\alpha )\parallel AB\\AB \subset (ABD)\\(\alpha )\cap (ABD) = PQ\end{array} \right. \)

\(\Rightarrow PQ\parallel AB\)

Ta có:

\(\left\{ \begin{array}{l}(\alpha )\parallel CD\\CD \subset (ACD)\\(\alpha )\cap (ACD) = MQ\end{array} \right. \)

\(\Rightarrow MQ\parallel CD\)

Do đó \(MN\parallel PQ\) và \(NP\parallel MQ\).

Vậy tứ giác \(MNPQ\) là hình bình hành.

LG b

Gọi \(O\) là giao điểm hai đường chéo của tứ giác \(MNPQ\). Tìm tập hợp các điểm \(O\) khi \(M\) di động trên đoạn \(AC\).

Phương pháp giải:

Sử dụng định lý Talet

Lời giải chi tiết:

Ta có \(MP\cap NQ=O\). Gọi \(I\) là trung điểm của \(CD\).

Trong tam giác \(ACD\) có \(MQ\parallel CD\) \(\Rightarrow AI\cap MQ=E, E\) là trung điểm của \(MQ\).

Trong tam giác \(BCD\) có \(NP\parallel CD\) \(\Rightarrow BI\cap NP=F, F\) là trung điểm của \(MQ\).

Khi đó \(EF\) là đường trung bình của hình bình hành \(MNPQ\) \(\Rightarrow EF\parallel MN\) và \(O\) là trung điểm của \(EF\).

Trong tam giác \(ABI\) có \(EF\parallel AB\), \(O\) là trung điểm của \(EF\) khi đó \(IO\cap AB=J, J\) là trung điểm của \(AB\).

\(\Rightarrow I, O, J\) thẳng hàng, \(O\) thuộc \(IJ\) cố định.

Vì \(M\) di động trên \(AC\) nên \(O\) chạy trong đoạn \(IJ\).

Vậy tập hợp các điểm \(O\) là đoạn \(IJ\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 2.21 trang 72 SBT hình học 11
Giải bài 2.21 trang 72 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên đoạn AB.một mặt phẳng...
Bài 2.19 trang 71 SBT hình học 11
Giải bài 2.19 trang 71 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn là AD và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD...
Bài 2.18 trang 71 SBT hình học 11
Giải bài 2.18 trang 71 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM...
Bài 2.17 trang 71 SBT hình học 11
Giải bài 2.17 trang 71 sách bài tập hình học 11. Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF...
Bài 2.16 trang 71 SBT hình học 11
Giải bài 2.16 trang 71 sách bài tập hình học 11. Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm của tam giác ACD và BCD. Chứng minh rằng G1G2 song song với các mặt phẳng (ABC) và (ABD).