Giải SBT toán hình học và đại số giải tích 11 cơ bản Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

Bài 1.21 trang 28 SBT hình học 11


Giải bài 1.21 trang 28 sách bài tập hình học 11. Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục.

Đề bài

Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục.

Phương pháp giải - Xem chi tiết

- Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).

Lời giải chi tiết

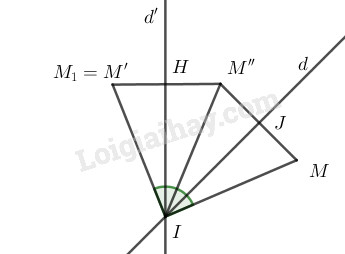
Gọi \(Q_{(I,\alpha)}\) là phép quay tâm \(I\) góc \(\alpha\). Lấy đường thẳng \(d\) bất kì qua \(I\). Gọi \(d’\) là ảnh của \(d\) qua phép quay tâm \(I\) góc \(\dfrac{\alpha}{2}\). Lấy điểm \(M\) bất kì và gọi \(M’=Q_{(I,\alpha)}(M)\). Gọi \(M’’\) là ảnh của \(M\) qua phép đối xứng qua trục \(d\). \(M_1\) là ảnh của \(M’’\) qua phép đối xứng qua trục \(d’\). Gọi \(J\) là giao của \(MM’\) với \(d\), \(H\) là giao của \(M’’M_1\) với \(d’\).

Khi đó ta có đẳng thức giữa các góc lượng giác sau:

\((IM,IM_1)\)

\(=(IM,IM’’)+(IM’’,IM_1)\)

\(=2(IJ,IM’’)+2(IM’’,IH)\)

\(=2(IJ,IH)=2\dfrac{\alpha}{2}=\alpha=(IM,IM’)\)

Từ đó suy ra \(M’\equiv M_1\). Như vậy \(M’\) có thể xem là ảnh của \(M\) sau khi thực hiện liên tiếp hai phép đối xứng qua hai trục \(d\) và \(d’\).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua