-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Trả lời câu hỏi 2 trang 33 SGK Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của hàm số ...
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^3}\; + {\rm{ }}3{x^2}\; - {\rm{ }}4\)
Nêu nhận xét về đồ thị của hàm số này với đồ thị của hàm số khảo sát trong Ví dụ 1.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
B1: Tìm TXĐ
B2: Bảng biến thiên
- Xét chiều biến thiên
+Tính \(y'\).
+ Tìm các điểm mà tại đó hàm số không xác định và nghiệm của \(y'=0\).
+ Xét dấu đạo hàm suy ra chiều biến thiên
- Tìm cực trị
- Tính các giới hạn,tiệm cận (nếu có).
- Lập bảng biến thiên
B3: Vẽ đồ thị
Lời giải chi tiết
TXĐ: \(D = \mathbb R.\)
Sự biến thiên:
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr
& \mathop {\lim }\limits_{x\to - \infty } y = + \infty \cr} \)
\(y’ = -3x^2 + 6x.\) Cho \(y’ = 0 ⇒ x = 0\) hoặc \(x = 2.\)
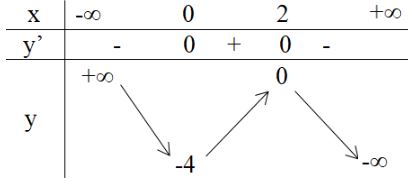
Bảng biến thiên
Hàm số đồng biến trên khoảng \((0,2)\)
Hàm số nghịch biến trên các khoảng \((-∞,0), (2,+ ∞).\)
Hàm số đạt cực đại bằng 0 tại \(x = 2.\)
Hàm số đạt cực tiểu bằng -4 tại \(x = 0.\)
Vẽ đồ thị hàm số
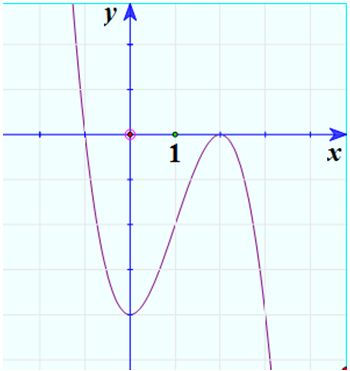
Nhận xét: hai đồ thị đối xứng nhau qua \(Oy.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Trả lời câu hỏi 3 trang 35 SGK Giải tích 12
- Trả lời câu hỏi 4 trang 36 SGK Giải tích 12
- Trả lời câu hỏi 5 trang 38 SGK Giải tích 12
- Trả lời câu hỏi 6 trang 42 SGK Giải tích 12
- Giải bài 1 trang 43 SGK Giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
