Giải SBT toán hình học và đại số 11 nâng cao Bài 5: Khoảng cách

Câu 69 trang 127 Sách bài tập Hình học 11 Nâng cao


Giải bài tập Câu 69 trang 127 Sách bài tập Hình học 11 Nâng cao

Đề bài

Đáy của hình chóp A.BCD là tam giác đều. Đường cao của hình chóp kẻ từ đỉnh A đi qua trung điểm H của cạnh CD. Cắt hình chóp đó bởi mặt phẳng song song với AB và CD và cách đỉnh B một khoảng bằng d. Tính diện tích thiết diện thu được, biết cạnh của tam giác đều BCD là a và \(AB = a\sqrt 2 \).

Lời giải chi tiết

  

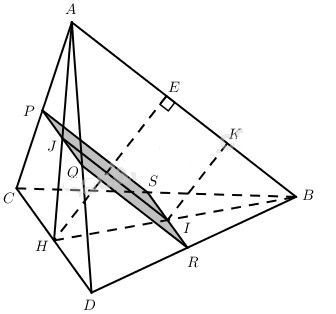
Dễ thấy thiết diện là hình bình hành PQRS. Mặt khác theo giả thiết \(C{\rm{D}} \bot \left( {AHB} \right)\) nên \(C{\rm{D}} \bot AB\). Vậy PQRS là hình chữ nhật.

Kẻ \(HE \bot AB\) thì \(HE \bot \left( {PQ{\rm{RS}}} \right)\). Kẻ IK // HE thì \(IK \bot \left( {PQ{\rm{RS}}} \right)\). Do AB // (PQRS) và \(d\left( {B;\left( {PQ{\rm{RS}}} \right)} \right) = d\) nên IK = d.

Ta có

\(HE = {{AH.HB} \over {AB}} = {{\sqrt {A{B^2} - B{H^2}} .HB} \over {AB}} = {{a\sqrt {15} } \over {4\sqrt 2 }}\)

Lại có

 \(\eqalign{  & {{IK} \over {HE}} = {{BI} \over {BH}} = {{R{\rm{S}}} \over {C{\rm{D}}}}  \cr  &  \Rightarrow R{\rm{S}} = {{da} \over {a\sqrt {15} }}.4\sqrt 2  = {{4\sqrt 2 d} \over {\sqrt {15} }};  \cr  & BI = {{IK.BH} \over {HE}} = {{d.{{a\sqrt 3 } \over 2}} \over {{{a\sqrt {15} } \over {4\sqrt 2 }}}} = {{2\sqrt 2 d} \over {\sqrt 5 }} \cr} \)

Mặt khác \({{IJ} \over {AB}} = {{HI} \over {HB}} = {{\left( {HB - IB} \right)} \over {HB}};\)

Từ đó \(IJ = {{AB\left( {HB - IB} \right)} \over {HB}} = {{\sqrt 2 \left( {a\sqrt {15}  - 4\sqrt 2 d} \right)} \over {\sqrt {15} }}\)

Vậy \({S_{PQ{\rm{RS}}}} = R{\rm{S}}.IJ = {8 \over {15}}d\left( {a\sqrt {15}  - 4\sqrt 2 d} \right)\) .

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store