Giải SBT toán hình học và đại số 11 nâng cao Bài 5: Khoảng cách

Câu 58 trang 126 Sách bài tập Hình học 11 Nâng cao


Giải bài tập Câu 58 trang 126 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình chóp A.ABCD có cạnh SA = x, tất cả các cạnh còn lại có độ dài bằng a.

a) Chứng minh rằng SAC là tam giác vuông.

b) Tính đường cao SH của hình chóp đã cho.

Lời giải chi tiết

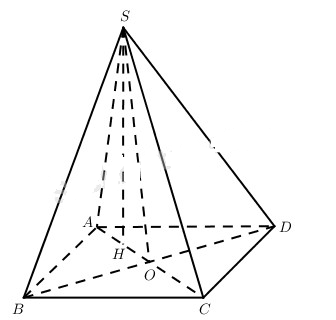
a) Gọi O là giao điểm của AC và BD thì \(OA = OC,OB = O{\rm{D}}\).

Vì \(SB = S{\rm{D}} = CB = C{\rm{D}}\) nên \(\Delta BC{\rm{D}} = \Delta B{\rm{SD}}\), từ đó \(SO = OC = OA\).

Vậy SAC là tam giác vuông tại S.

b) \(\left. \matrix{  AC \bot B{\rm{D}} \hfill \cr  {\rm{SO}} \bot {\rm{BD}} \hfill \cr}  \right\} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\),

từ đó \(\left( {SAC} \right) \bot \left( {ABC{\rm{D}}} \right)\).

Vậy nếu kẻ đường cao SH của tam giác SAC thì \(SH \bot \left( {ABC{\rm{D}}} \right)\),

do đó \(d\left( {S;mp\left( {ABC{\rm{D}}} \right)} \right) = SH = {{SA.SC} \over {AC}} = {{a.x} \over {\sqrt {{a^2} + {x^2}} }}\).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store