Câu 61 trang 126 Sách bài tập Hình học 11 Nâng cao

Giải bài tập Câu 61 trang 126 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên SAB là tam giác cân tại S và mp(SAB) vuông góc với mp(ABCD), cạnh SC tạo với mặt phẳng đáy góc α. Tính:

a) Chiều cao của hình chóp S.ABCD;

b) Khoảng cách từ chân đường cao hình chóp đến mặt phẳng (SCD);

c) Diện tích thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng trung trực của cạnh BC.

Lời giải chi tiết

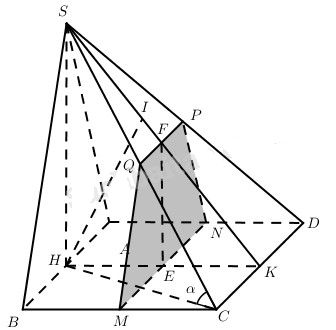
a) Gọi H là trung điểm của AB thì \(SH \bot AB\), từ đó \(SH \bot \left( {ABC{\rm{D}}} \right)\). Vậy khoảng cách từ S đến mp(ABCD) là SH, đó là chiều cao của hình chóp.

Ta có \(SH = HC\tan \alpha \),

mặt khác \(H{C^2} = B{H^2} + B{C^2} = {{5{{\rm{a}}^2}} \over 4}\).

hay \(HC = {{a\sqrt 5 } \over 2}\).

Vậy \(SH = {{a\sqrt 5 } \over 2}\tan \alpha \).

b) Gọi K là trung điểm của CD thì \(C{\rm{D}} \bot \left( {SHK} \right)\), từ đó \(\left( {SC{\rm{D}}} \right) \bot \left( {SHK} \right)\). Vậy nếu kẻ đường cao HI của tam giác SHK thì HI là khoảng cách từ H đến mp(SCD). Ta có:

\(\eqalign{ & HI = {{H{\rm{S}}.HK} \over {SK}} = {{{{a\sqrt 5 } \over 2}\tan \alpha .a} \over {\sqrt {{{5{{\rm{a}}^2}} \over 4}{{\tan }^2}\alpha + {a^2}} }} \cr & = {{a\sqrt 5 \tan \alpha } \over {\sqrt {5{{\tan }^2}\alpha + 4} }} \cr} \)

c) Vì SH và CD cùng vuông góc với BC nên SH, CD song song với mặt phẳng trung trực (R) của BC. Khi đó:

\(\left( R \right) \cap \left( {ABC{\rm{D}}} \right) = MN\) với MN // CD và M, N lần lượt là trung điểm của BC, AD.

\(\left( R \right) \cap \left( {SHK} \right) = EF\), EF // SH, E là trung điểm của MN.

\(\left( R \right) \cap \left( {SC{\rm{D}}} \right) = PQ\), PQ đi qua điểm F và PQ // CD. Thiết diện MNPQ là hình thang cân.

Ta có

\(\eqalign{ & {S_{MNPQ}} = {1 \over 2}\left( {MN + PQ} \right).EF \cr & = {1 \over 2}\left( {a + {a \over 2}} \right).{{a\sqrt 5 } \over 4}\tan \alpha \cr & = {{3{a^2}\sqrt 5 } \over {16}}\tan \alpha \cr} \).

Loigiaihay.com