Câu 5.50 trang 187 sách bài tập Đại số và Giải tích 11 Nâng cao

Chứng minh rằng tiếp tuyến tại điểm bất kì của đồ thị hàm số, cắt trục tung tại một điểm cách đều tiếp điểm và gốc tọa độ.

Đề bài

Chứng minh rằng tiếp tuyến tại điểm bất kì của đồ thị hàm số

\(y = {1 \over 2}\sqrt {x - 4{x^2}} \,\,\,\,(C)\)

Cắt trục tung tại một điểm cách đều tiếp điểm và gốc tọa độ.

Lời giải chi tiết

Để hàm số có đạo hàm thì ta phải có

\(x - 4{x^2} > 0 \Leftrightarrow 0 < x < {1 \over 4}.\)

Với điều kiện \(0 < x < {1 \over 4},\) ta có

\(y' = {{1 - 8x} \over {4\sqrt {x - 4{x^2}} }}.\)

Gọi \({M_0}\left( {{x_0};{y_0}} \right)\) là một điểm tuy ý thuộc đồ thị(C) ; ta có \({y_0} = {1 \over 2}\sqrt {{x_0} - 4x_0^2,} \) \(y' = {{1 - 8{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }}\). Vậy phương trình tiếp tuyến tại \({M_0}\left( {{x_0},{y_0}} \right)\) là

\(y = {{1 - 8{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }}\left( {x - {x_0}} \right) + {1 \over 2}\sqrt {{x_0} - 4x_0^2} \)

Tiếp tuyến này cắt trục tung tại điểm T có tung độ là

\(\eqalign{& {y_T} = {{1 - 8{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }}\left( {0 - {x_0}} \right) + {1 \over 2}\sqrt {{x_0} - 4x_0^2} \cr& \,\,\,\,\, = {{\left( {1 - 8{x_0}} \right)\left( { - {x_0}} \right) + 2\left( {{x_0} - 4x_0^2} \right)} \over {\sqrt {{x_0} - 4x_0^2} }} \cr& = {{{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }} > 0 \cr} \)

Khoảng cách \(T{M_0}\) được tính bởi công thức

\(\eqalign{ T{M_0} &= {\left( {{x_0} - 0} \right)^2} \cr& + {\left( {{1 \over 2}\sqrt {{x_0} - 4x_0^2} - {{{x_0}} \over {\sqrt {{x_0} - 4x_0^2} }}} \right)^2} \cr& = x_0^2{\left( {{{2\left( {{x_0} - 4x_0^2} \right) - {x_0}} \over {\sqrt {{x_0} - 4x_0^2} }}} \right)^2} \cr& = x_0^2 + {{{{\left( {{x_0} - 8x_0^2} \right)}^2}} \over {16\left( {{x_0} - 4x_0^2} \right)}} \cr& = {{16x_0^3 - 64x_0^4 + x_0^2 - 16x_0^3 + 64x_0^4} \over {16\left( {{x_0} - 4x_0^2} \right)}} \cr& = {{x_0^2} \over {16\left( {{x_0} - 4x_0^2} \right)}} \cr} \)

Vậy

\(\left| {T{M_0}} \right| = {{{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }} = \left| {TO} \right| = {y_T}\)

Điều này chứng tỏ, điểm T cách đều tiếp điểm \({M_0}\) và gốc tọa độ O.

Chú ý: Có thể chứng minh bào toán này bằng phương pháp hình học như sau:

Với \(0 \le x{1 \over 4}\) thì \(y \ge 0\) ta có

\(\eqalign{& y = {1 \over 2}\sqrt {x - 4{x^2}} \Leftrightarrow 4{y^2} + 4{x^2} - x = 0 \cr& \Leftrightarrow {x^2} + {x \over 4} + {y^2} = 0 \cr& \Leftrightarrow {\left( {x - {1 \over 8}} \right)^2} + {y^2} = {\left( {{1 \over 8}} \right)^2} \cr} \)

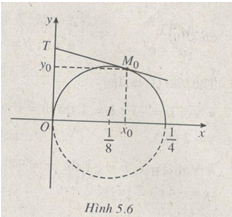
Vậy đồ thị (C) là phần đường tròn thuộc góc phần tư thứ nhất (vì \(x \ge 0\) và \(y \ge 0\)) tâm \(I\left( {{1 \over 8};0} \right)\), bán kính \(R = {1 \over 8}\) (h.5.6)

Áp dụng tính chất: từ một điểm T ngoài đường tròn, kẻ được hai tiếp tuyến với đường tròn là \(TM_0\) và TO và ta có \(|TM_0|=|TO|\) (đpcm).