-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Khảo sát và vẽ đồ thị hàm số bậc ba
Các bước khảo sát và vẽ đồ thị hàm số. Câu 1 khảo sát hàm số là câu hỏi mặc định có trong mỗi đề thi tuyển sinh môn toán, cùng xem lại các bước thật kỹ nhé.
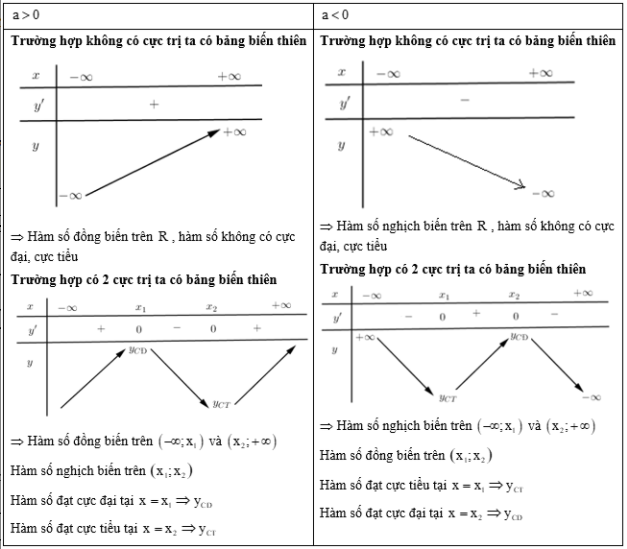
Hàm số bậc ba: \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\)
+) TXĐ: $D = R$
+) Sự biến thiên:
\(y' = 3a{x^2} + 2bx + c\)
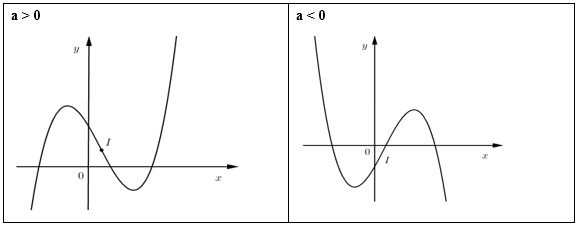
\(y' = 0\) có hai nghiệm phân biệt \({x_1},{x_2} \Rightarrow \) có cực trị.
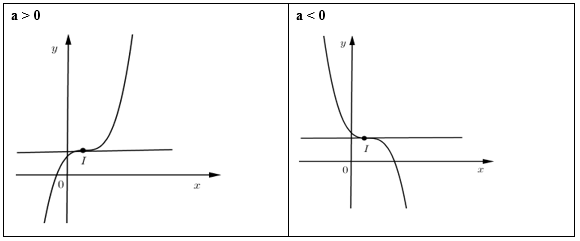
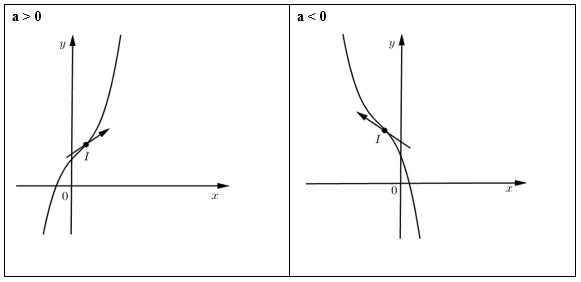
\(y' = 0\) vô nghiệm hoặc có nghiệm kép \( \Rightarrow \) không có cực trị.
+) Đồ thị:
- Điểm uốn \(I\left( {{x_0};{y_0}} \right)\) với \({x_0}\) là nghiệm của phương trình \(y'' = 0\) và \({y_0} = f\left( {{x_0}} \right)\).
TH1: \(y' = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' = {b^2} - 3ac > 0\)
TH2:\(y' = 0\) có nghiệm kép \( \Leftrightarrow \Delta ' = {b^2} - 3ac = 0\)
TH3: \(y' = 0\) vô nghiệm \( \Leftrightarrow \Delta ' = {b^2} - 3ac < 0\)
Bình luận
Chia sẻ
- Khảo sát và vẽ đồ thị hàm bậc bốn trùng phương
- Khảo sát và vẽ đồ thị hàm phân thức hữu tỉ
- Các dạng toán về khảo sát hàm số bậc ba, bậc bốn trùng phương
- Giải bài 9 trang 44 SGK Giải tích 12
- Giải bài 8 trang 44 SGK Giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
