-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Bài 9 trang 28 SGK Hình học 12
Cho hình hộp ABCD.A'B'C'D'. Tỉ số thể tích của khối tứ diện ACB'D' và khối hộp ABCD.A'B'C'D' bằng:
Đề bài
Cho hình hộp \(ABCD.A'B'C'D'\). Tỉ số thể tích của khối tứ diện \(ACB'D'\) và khối hộp \(ABCD.A'B'C'D'\) bằng:
(A) \(\displaystyle {1 \over 2}\) (B) \(\displaystyle{1 \over 3}\)
(C) \(\displaystyle{1 \over 4}\) (D) \(\displaystyle{1 \over 6}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Phân chia và lắp ghép các khối đa diện.
Hình hộp được chia thành \(5\) khối \(A’.AB'D';\, B.AB’C;\, C’.B’CD’;\, D.ACD’ \) và \(ACB’D’.\)
Lời giải chi tiết
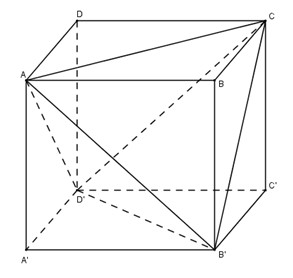
Giả sử diện tích đáy hình hộp là: \(S\) chiều cao là \(h\)
Thể tích hình hộp là \(V=Sh\)
Hình hộp được chia thành \(5\) khối tứ diện \(A’.AB'D';\) \( B.AB’C;;\) \( C’.B’CD’;\) \( D.ACD’\) và \(ACB’D’.\)
Ta có:
\({V_{A'.AB'D'}} = {V_{A.A'B'D'}}\) \( = \dfrac{1}{3}.h.{S_{A'B'D'}} = \dfrac{1}{3}h.\dfrac{1}{2}S\) \( = \dfrac{1}{6}.Sh = \dfrac{1}{6}.V\)
Tương tự \({V_{B.AB'C}} = {V_{C'.B'CD'}} = {V_{D.ACD'}} = \dfrac{1}{6}V\)
Do đó
\({V_{ACB'D'}} = V - \;({V_{A'AB'D'}} + {V_{BAB'C}} + {V_{C'B'CD'}} + {V_{DACD'}})\)
\(\begin{array}{l} = V - \left( {\dfrac{1}{6}V + \dfrac{1}{6}V + \dfrac{1}{6}V + \dfrac{1}{6}V} \right)\\ = V - \dfrac{2}{3}V\\ = \dfrac{1}{3}V\\ \Rightarrow \dfrac{{{V_{ACB'D'}}}}{V} = \dfrac{1}{3}\end{array}\)
Chọn (B).
loigiaihay.com
Bình luận
Chia sẻ
- Bài 10 trang 28 SGK Hình học 12
- Bài 8 trang 28 SGK Hình học 12
- Bài 7 trang 28 SGK Hình học 12
- Bài 6 trang 28 SGK Hình học 12
- Bài 5 trang 28 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
